Nollställen i en funktion
Hej, jag ska hitta alla nollställen mellan 0 < x < 180 i funktionen nedan.

1, Jag började med att faktorisera ut sin(2x) ur täljaren, och då den är noll så är värdet för hela funktionen noll. sin(2x) = 0 så x=90
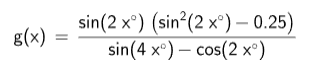
2, Jag antog då att de andra nollställen finns då sin^2(2x) = 0.25 då det åter igen blir multiplikation med noll. Så jag löste bara ekvationen sin^2(2x) = 0.25, då blir x=15, 75, 105 och 165. Jag förväntade mig att om jag stoppar in alla dessa värden i funktionen skulle jag få f(x) = 0, men de enda som faktiskt funkar är x = 90, 105, 165. se grafen:

Vad exakt var felet vid punkt 2? x=15 och x=75 ger 1/4 och -1/4.
Jag har en suspicion att det har o göra med nämnaren.
Mvh
Hej, det stämmer att problemet uppkommer i samband med nämnaren. Ovan så har du funnit de x som gör att täljaren ger värdet 0. Man kan se detta som ett "nödvändigt" villkor för att det ska finnas ett nollställe till funktionen h(x) där. Problemet är att då nämnaren kan bli 0 så får man en kvot 0/0 som inte är definierad, och då ej är ett nollställe. Man får då kolla när även nämnaren är 0, vilket blir vid just x=15 och x=75 som gör att dessa värden inte löser ekvationen. Nämnaren har vidare nollställena x=45 och x=135 vilket man ser från figuren, eller alternativt löser ut detta, även om detta inte är nödvändigt för uppgiften.

