NOG Uppgift Liksidig Triangel
Jag tror svaret är D eftersom jag vet inte hur jag kan beräkna x
Hej.
Börja med att beräkna vinkeln y.

Arup skrev:Jag tror svaret är D eftersom jag vet inte hur jag kan beräkna x
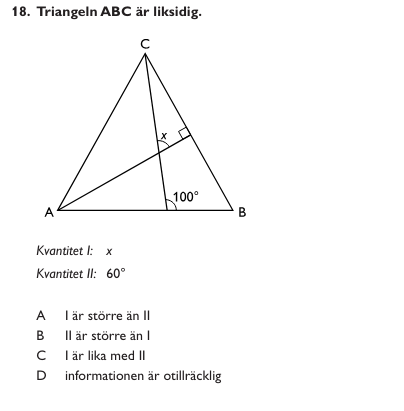
I en liksidig triangel är alla vinklar ______° därmed är vinkeln B = ______°
Vinkelsumman i en triangel är _____° varför vinkeln y = _____°
Vinkelsumman i en triangel är _____° varför vinkeln x = _____°
Jag undrar om sträckan eller linjen som står bredvid 100˚ vinkeln är en bisektris ?
Nej, det är den inte, döremot är linjen som bildar en rät vinkel en bisektris.
Arup skrev:Jag undrar om sträckan eller linjen som står bredvid 100˚ vinkeln är en bisektris ?
Du behöver inte använda bisektriser för att lösa uppgiften.
Förstod du tipsen som du fick i svar #3 och svar #4?
jag förstod inte till 100 % hur man skulle kunna bestämma vinkel y
Min tolkning är att jag löser ut Y så här :
Eftersom triangeln ABC är liksidig så vet du vad vinkeln vid B är.
Kommer du vidare då?
Läs annars svar #4 igen.
Du behöver inte ta till något avancerat för att bestämma samtliga vinklar i figuren. Givet ABC:s liksidighet, de givna vinklarna, samt att du vet vinkelsumman av en triangel och en fyrhörning, har du allt du behöver.
Fyll i det du vet och beräkna en vinkel i taget. Till slut känner du samtliga.
Så här har jag tänkt 
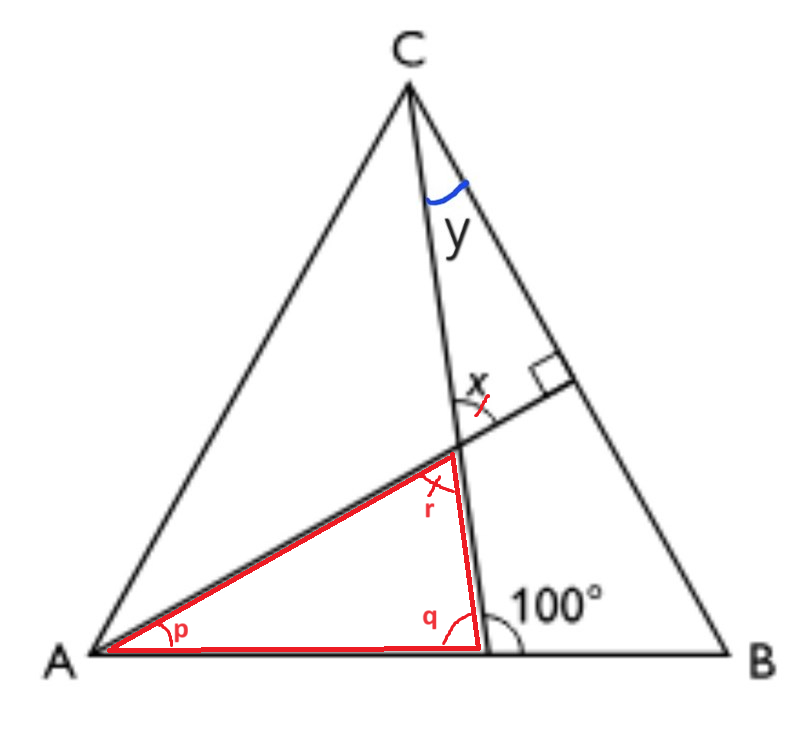
Nu har du använt symbolen y till två olika vinklar. Först röd (60°+60°+y = 180°), sedan blå (y+x+90° = 180°), se bild.

Ok, kan vinkeln C uttryckas som
Yngve jag trodde man skulle ställa upp ett ekv systsem
Trinity2 skrev:Arup skrev:Jag tror svaret är D eftersom jag vet inte hur jag kan beräkna x
I en liksidig triangel är alla vinklar ______° därmed är vinkeln B = ______°
Vinkelsumman i en triangel är _____° varför vinkeln y = _____°
Vinkelsumman i en triangel är _____° varför vinkeln x = _____°
Jag förstår inte hur Trinity menade med de två sista raderna
Arup skrev:Ok, kan vinkeln C uttryckas som
Det beror på vad du menar med "vinkeln C".
C är ett hörn, inte en vinkel.
Se bild, det finns tre vinklar vid C.
- ACB. Denna vinkel är 60°.
- DCF. Denna vinkel kallar vi y.
- ACD. Denna vinkel är 60°-y, men vi behöver inte använda den
Tips på väg framåt:
- Beräkna vinkeln ABC med hjälp av att triangeln ABC är liksidig.
- Beräkna vinkeln y, med hjälp av att triangeln ECB har känd vinkelsumma och två kända vinklar.
- Beräkna x med hjälp av att triangeln CDF har känd vinkelsumma och två kända vinklar.

Yngve hur kan jag beräkna vinkeln ABC om det finns en linje som delar vinkeln A och även I hörnet C ? Även om jag vet att vinkelsumman i en triangel är 180
Aha, du kanske inte är med på vad beteckningen "vinkeln ABC" betyder?
Det betyder "Vinkeln mellan vinkelbenet som går från B till A och vinkelbenet som går från B till C".
Då spelar det ingen roll om det går ut andra vinkelben från vare sig A, B eller C. Det är ändå (nästan helt) entydigt.
Yngve skrev:...
I det här fallet skulle man kunna kalla vinkeln ABC för bara B, eftersom det bara finns en enda vinkel i hörnet B. Däremot skulle det vara svårt att kalla någon vinkel för A, eftersom det skulle kunna vara antingen vinklen CAB eller vinkeln CAD eller vinkeln DAB som man menar.
När du sade Vibkeln ABC så tolkade jag det som Triangel ABC
Vilken lång tråd för ett ganska enkelt geometriskt problem.
Jag gör den ett inlägg längre, men kan kanske hjälpa till.
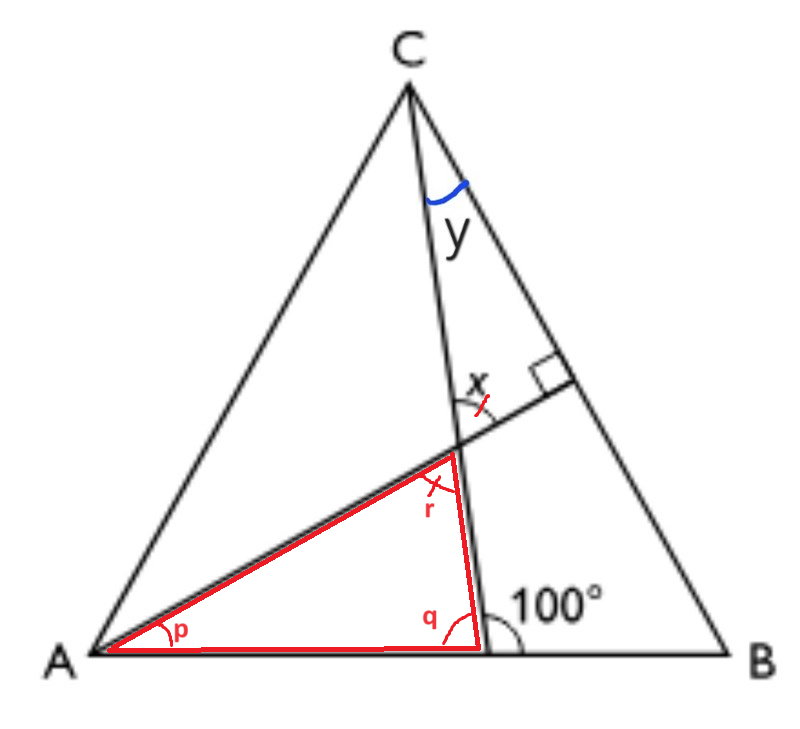
- ABC är liksidig, vilket gör att du vet vinklarna A, B och C (som förstås också är lika).
- Konstatera att höjden som är dragen i rät vinkel från BC till A, delar vinkeln A i två lika delar.
- Nu vet du båda halvorna av vinkeln A. Vi kallar den ena för p.
- Från AB är dragen en linje till C. Den högra vinkeln är 100 grader. Det ger dig den vänstra, som vi kallar q.
- Givet p och q, kan du nu räkna ut r, som är lika stor som x.
Det är allt du behöver och svårare än så är det inte.
oj, jag hade helt glömt bort att vinkel x=vinkelr
Du har ett formelblad, som du kan titta igenom för att leta inspiration. Det var ett av mina standardknep när jag läste på gymnasiet - särskilt i fysik , men även i matte.
Arup skrev:När du sade Vibkeln ABC så tolkade jag det som Triangel ABC
OK, men hänger du nu med på metoden jag beskrev i svar #16 (som för övrigt är samma som Trinity2 beskrev i svar #4)?
====
Son du ser går det även att lösa problemet med den metod som sictransit visar i svar #21.
Vilken man föredrar är en smaksak.
Är det rätt nu.
Jag följde Sictransit:s metod.

Arup skrev:Är det rätt nu.
Jag följde Sictransit:s metod.
Rätt! Men det finns också andra sätt att lösa problemet. Man kan lösa uppgiften utan att dela A i två vinklar, dvs använda dig av bisektris.
Bisektris satsen ?
När man gör HP vill man helst kunna lösa uppgiften snabbt för att spara på tiden
Arup skrev:Bisektris satsen ?
När man gör HP vill man helst kunna lösa uppgiften snabbt för att spara på tiden
Okej, jag förstår nu, tack!
sictransit skrev:Vilken lång tråd för ett ganska enkelt geometriskt problem.
Jag gör den ett inlägg längre, men kan kanske hjälpa till.
- ABC är liksidig, vilket gör att du vet vinklarna A, B och C (som förstås också är lika).
- Konstatera att höjden som är dragen i rät vinkel från BC till A, delar vinkeln A i två lika delar.
- Nu vet du båda halvorna av vinkeln A. Vi kallar den ena för p.
- Från AB är dragen en linje till C. Den högra vinkeln är 100 grader. Det ger dig den vänstra, som vi kallar q.
- Givet p och q, kan du nu räkna ut r, som är lika stor som x.
Det är allt du behöver och svårare än så är det inte.
Jag håller med dig nu om att problemet var mycket enklare än vad jag hade för mig
Arup skrev:Bisektris satsen ?
När man gör HP vill man helst kunna lösa uppgiften snabbt för att spara på tiden
Du har fått tips på en enkel metod i svar #16 och en annan enkel metod i svar #22.
Ingen av dessa metoder använder bisektrissatsen eller någon annan komplicerad formel.
ok jag ska kika på flera lösningsmetoder
Arup skrev:ok jag ska kika på flera lösningsmetoder
Det finns som andra sagt många vägar mot målet när det ändå ges rätt mycket information i uppgiften.
Du kan utnyttja att en fyrhörnings vinkelsumma är 360 grader.
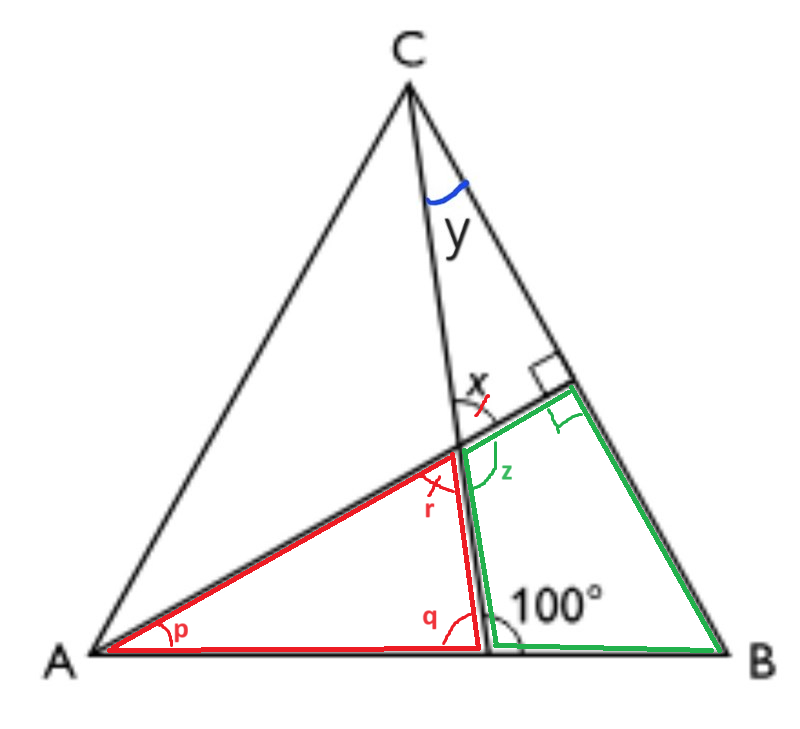
Med samma resonemang som i mitt tidigare inlägg är vinkeln B 60 grader.
Då känner du tre av de fyra vinklarna i den gröna fyrhörningen.
Återstår att beräkna vinkeln z.
Du vet sedan att x+z=180.
Hur vet vi att vinklarna x=r. Är det för att de är vertikal vinklar ?
Ja, det stämmer. Du kan läsa mer om det t.ex. här.
Prövade Sictransit:s metod med fyrhörningen

Snyggt.
En enda kommentar är att du bör kalla fyrhörningen EFGB istället för EFG.
Oops såg lite för snabbt