nodlinje
Hej! Kan någon hjälpa mig med den här frågan?
Två ljudkällor A och B befinner sig 5 m från varandra, i ett fullständigt ljudisolerat rum dvs inget ljud kan studsar. Ljudets hastighet i rummet är 315 m/s. Båda ljudkällor sänder ut en ton på 115 Hz . Glöm inte att båda två ljudkällor A och B sänder ut i fas med varandra.
a) Rita hur situationen ser ut och rita ut de 3 punkter i rummet där det är tyst. (skalaenligt)
b) Vad är våglängden på ljudet?
c) Varför ljudisolerat rum krävs för att detta fenomen skall uppkomma?
d) Rita en nodlinje där det är tyst
Är det rätt?
b)
Hur ska fortsätt gör a
Marko skrev:Hur ska fortsätt gör a
Du ska rita hur situationen ser ut.
Pieter Kuiper skrev:Marko skrev:Hur ska fortsätt gör a
Du ska rita hur situationen ser ut.
Jag fattar inte hur ska rita upp den, få man använda Geogbra?
Men hur ska veta de 3 punkter i rummet där det är tyst?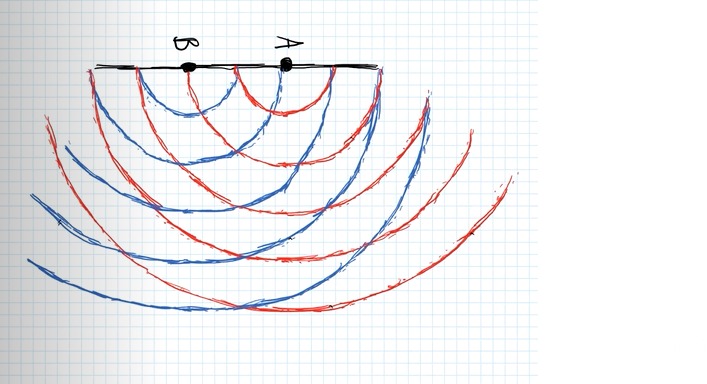
Som uppgiften säger ska ritningen vara skalenlig, där alltså våglängden är avståndet mellan högtalarna stämmer med varandra.
Står det i uppgiften "de tre punkter i rummet"? Med bestämd artikel? Det skulle vara konstigt.
Vad måste gälla på ställen där det blir relativt tyst?
Pieter Kuiper skrev:Som uppgiften säger ska ritningen vara skalenlig, där alltså våglängden är avståndet mellan högtalarna stämmer med varandra.
Står det i uppgiften "de tre punkter i rummet"? Med bestämd artikel? Det skulle vara konstigt.
Vad måste gälla på ställen där det blir relativt tyst?
- Hur ska göra våglängden är avståndet mellan högtalarna stämmer med varandra?
- Ja det står u uppgiften "de tre punkter i rummet"
- På ställen där det blir relativt tyst, det vill säga nodpunkterna, måste det gälla konstruktiv interferens mellan de två ljudvågorna från ljudkällorna A och B? är det rätt?
Marko skrev:- Hur ska göra våglängden är avståndet mellan högtalarna stämmer med varandra?
- Ja det står u uppgiften "de tre punkter i rummet"
- På ställen där det blir relativt tyst, det vill säga nodpunkterna, måste det gälla konstruktiv interferens mellan de två ljudvågorna från ljudkällorna A och B? är det rätt?
Du har ju en våglängd. Om man ritar vågfronter som du nog gör det är det avståndet mellan cirklarna. Och det ska då vara på samma skala som avståndet mellan vågkällorna.
Detta med "de tre punkter i rummet" är konstigt. Det finns nodlinjer (eller nodytor) med oändligt många punkter. Det kan finnas sådana punkter på linjen mellan A och B, kanske menar de det.
Nej, det det blir relativt tyst menar du nog destruktiv interferens. Vad är villkoret för det?
Pieter Kuiper skrev:Marko skrev:- Hur ska göra våglängden är avståndet mellan högtalarna stämmer med varandra?
- Ja det står u uppgiften "de tre punkter i rummet"
- På ställen där det blir relativt tyst, det vill säga nodpunkterna, måste det gälla konstruktiv interferens mellan de två ljudvågorna från ljudkällorna A och B? är det rätt?Du har ju en våglängd. Om man ritar vågfronter som du nog gör det är det avståndet mellan cirklarna. Och det ska då vara på samma skala som avståndet mellan vågkällorna.
Detta med "de tre punkter i rummet" är konstigt. Det finns nodlinjer (eller nodytor) med oändligt många punkter. Det kan finnas sådana punkter på linjen mellan A och B, kanske menar de det.
Nej, det det blir relativt tyst menar du nog destruktiv interferens. Vad är villkoret för det?
-Menar du så här med avståndet mellan cirklarna och samma skala som avståndet mellan vågkällorna?
- Kan man rita de punkter som jag gjort med grön färg? 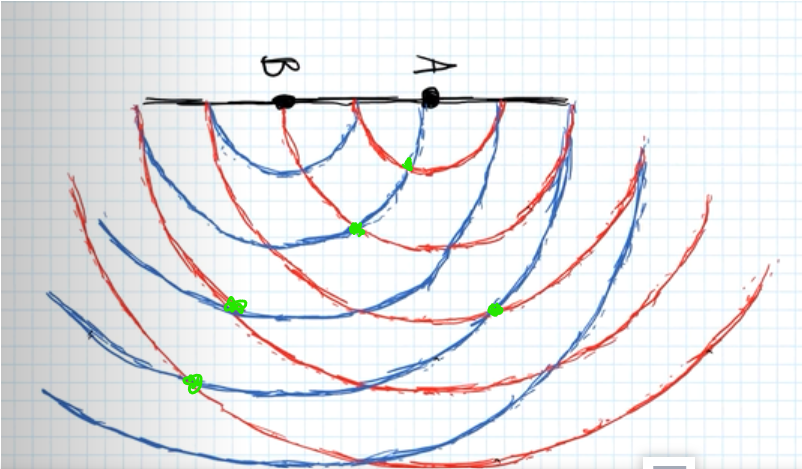
- Jag vet inte
Marko skrev (i PM):Pieter Kuiper skrev:Nej, där det blir relativt tyst menar du nog destruktiv interferens. Vad är villkoret för det?
- Destruktiv interferens då Δs=(k+(1/2))⋅λ
Så börja med att markera åtminstone en punkt där skillnaden mellan avstånden är en halv våglängd.
Sedan åtminstone en punkt där skillnaden är 1,5 λ.
Pieter Kuiper skrev:Marko skrev (i PM):Pieter Kuiper skrev:Nej, där det blir relativt tyst menar du nog destruktiv interferens. Vad är villkoret för det?
- Destruktiv interferens då Δs=(k+(1/2))⋅λ
Så börja med att markera åtminstone en punkt där skillnaden mellan avstånden är en halv våglängd.
Sedan åtminstone en punkt där skillnaden är 1,5 λ.
K = 0 Δs = 1,365
K = 1 Δs = 4,095
K = 2 Δs= 6,825 Men hur vet jag var punkten ska placeras?
Men hur vet jag var punkten ska placeras?
Jag försökte placera de punkter (gröna färg)så här:
Marko skrev:Pieter Kuiper skrev:Marko skrev (i PM):- Destruktiv interferens då Δs=(k+(1/2))⋅λ
Så börja med att markera åtminstone en punkt där skillnaden mellan avstånden är en halv våglängd.
Sedan åtminstone en punkt där skillnaden är 1,5 λ.K = 0 Δs = 1,365
K = 1 Δs = 4,095
K = 2 Δs= 6,825
Men hur vet jag var punkten ska placeras?
Jag försökte placera de punkter (gröna färg)så här:
Dina ritningar är inte skalenliga.
Alltså: ∆s = 1,365 är en längd med en enhet.
Avståndet mellan A och B är given som 5 meter.
Det enklaste är att hitta sådana punkter på linjen mellan A och B (som jag skrev i #9).
Pieter Kuiper skrev:Marko skrev:Pieter Kuiper skrev:Marko skrev (i PM):- Destruktiv interferens då Δs=(k+(1/2))⋅λ
Så börja med att markera åtminstone en punkt där skillnaden mellan avstånden är en halv våglängd.
Sedan åtminstone en punkt där skillnaden är 1,5 λ.K = 0 Δs = 1,365
K = 1 Δs = 4,095
K = 2 Δs= 6,825
Men hur vet jag var punkten ska placeras?
Jag försökte placera de punkter (gröna färg)så här:Dina ritningar är inte skalenliga.
Alltså: ∆s = 1,365 är en längd med en enhet.
Avståndet mellan A och B är given som 5 meter.
Det enklaste är att hitta sådana punkter på linjen mellan A och B (som jag skrev i #9).
Den första punkt är:
Δs = 1,365 och Δs = 4,095 ligger mellan A och B
Δs= 6,825 Ska det vara utan för avståndet mellan A och B
Är det rätt nu?
Pieter Kuiper skrev:Marko skrev:Pieter Kuiper skrev:Marko skrev (i PM):- Destruktiv interferens då Δs=(k+(1/2))⋅λ
Så börja med att markera åtminstone en punkt där skillnaden mellan avstånden är en halv våglängd.
Sedan åtminstone en punkt där skillnaden är 1,5 λ.K = 0 Δs = 1,365
K = 1 Δs = 4,095
K = 2 Δs= 6,825
Men hur vet jag var punkten ska placeras?
Jag försökte placera de punkter (gröna färg)så här:Dina ritningar är inte skalenliga.
Alltså: ∆s = 1,365 är en längd med en enhet.
Avståndet mellan A och B är given som 5 meter.
Det enklaste är att hitta sådana punkter på linjen mellan A och B (som jag skrev i #9).
Alltså hur ska jag rita skalenlig?
Marko skrev:Pieter Kuiper skrev:Marko skrev:Pieter Kuiper skrev:Marko skrev (i PM):- Destruktiv interferens då Δs=(k+(1/2))⋅λ
Så börja med att markera åtminstone en punkt där skillnaden mellan avstånden är en halv våglängd.
Sedan åtminstone en punkt där skillnaden är 1,5 λ.K = 0 Δs = 1,365
K = 1 Δs = 4,095
K = 2 Δs= 6,825
Men hur vet jag var punkten ska placeras?
Jag försökte placera de punkter (gröna färg)så här:Dina ritningar är inte skalenliga.
Alltså: ∆s = 1,365 är en längd med en enhet.
Avståndet mellan A och B är given som 5 meter.
Det enklaste är att hitta sådana punkter på linjen mellan A och B (som jag skrev i #9).
Den första punkt är:
Δs = 1,365 och Δs = 4,095 ligger mellan A och B
Δs= 6,825 Ska det vara utan för avståndet mellan A och B
Är det rätt nu?
Du ritade inte. Du tog en bild (källorna heter P och Q) där avståndet mellan källorna är 1½ våglängd. Det stämmer ungefär med uppgiftens mått, men inte noggrant nog.
Sedan markerade du tre gröna pluppar. Kan du förklara varför du ritade dem på dessa ställen?
Du skrev igen Δs utan enheter, jag vet inte om det är ok för din lärare. Men nodlinjen med Δs = 4,095 skulle ligga väldigt nära källorna (ungefär bara en halv meter) om avståndet är i meter.
Pieter Kuiper skrev:Marko skrev:Pieter Kuiper skrev:Marko skrev:Pieter Kuiper skrev:Marko skrev (i PM):- Destruktiv interferens då Δs=(k+(1/2))⋅λ
Så börja med att markera åtminstone en punkt där skillnaden mellan avstånden är en halv våglängd.
Sedan åtminstone en punkt där skillnaden är 1,5 λ.K = 0 Δs = 1,365
K = 1 Δs = 4,095
K = 2 Δs= 6,825
Men hur vet jag var punkten ska placeras?
Jag försökte placera de punkter (gröna färg)så här:Dina ritningar är inte skalenliga.
Alltså: ∆s = 1,365 är en längd med en enhet.
Avståndet mellan A och B är given som 5 meter.
Det enklaste är att hitta sådana punkter på linjen mellan A och B (som jag skrev i #9).
Den första punkt är:
Δs = 1,365 och Δs = 4,095 ligger mellan A och B
Δs= 6,825 Ska det vara utan för avståndet mellan A och B
Är det rätt nu?Du ritade inte. Du tog en bild (källorna heter P och Q) där avståndet mellan källorna är 1½ våglängd. Det stämmer ungefär med uppgiftens mått, men inte noggrant nog.
Sedan markerade du tre gröna pluppar. Kan du förklara varför du ritade dem på dessa ställen?
Du skrev igen Δs utan enheter, jag vet inte om det är ok för din lärare. Men nodlinjen med Δs = 4,095 skulle ligga väldigt nära källorna (ungefär bara en halv meter) om avståndet är i meter.
Jag ger upp. Jag försökte lösa det, men det går inte. Kan du snälla svara på frågan så att jag kan lära mig?
Marko skrev:Jag ger upp. Jag försökte lösa det, men det går inte. Kan du snälla svara på frågan så att jag kan lära mig?
Varför skulle inte det gå? Men jag får väl vara tydligare än i #13.
På linjen mellan A och B finns två punkter där ∆s = λ/2 = 1,37 m.
Ett sätt att lösa det är med ett ekvationssystem, ekvationerna är enkla.
Kalla avståndet till A a och till B b.
Då gäller a + b = 5 meter och a - b = 1,37 meter.
Bestäm lösningen. Och rita.
Bestäm även den andra punkten där ∆s = λ/2.




