Newton Raphson metoden - hittar man alltid den rot till ekvationen som man söker?

Kika på följande skiss av en kurva:

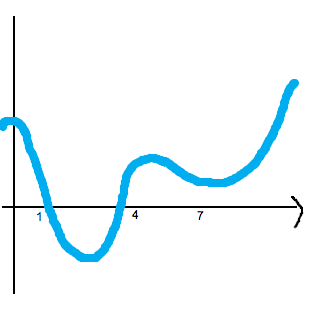
NR kan ses som en boll som attraheras av x-axeln; den rullar åt det håll då den kommer närmast x-axeln. Om vi startar bollen vid x = 4 kommer vi att hitta en rot, men vad händer med bollen om vi startar den då x = 7?

Jag förstår inte riktigt vad din graf visar. Vad är NR? 

Är det en boll som rullar då den kommer närmast x-axeln? För jag förstår inte "den rullar åt det håll..." ?

Den är i princip garanterad att fungera så länge startgissningen är tillräckligt nära roten man letar efter.

Hur nära man måste vara beror på hur mycket funktionen varierar runt roten, om dess derivata eller värde oscillerar eller konvergerar mot något.

Men är du för långt bort vid startgissningen så kan du antingen landa i en annan rot en den den du sökte, fastna i en loop som inte konvergerar mot något, eller hamna i ett olösbart delsteg om man råkade pricka en punkt där $f'(x) = 0$ och därmed tangenten aldrig skär x-axeln. 

Ah, det var kanske inte världens tydligaste bild, tänk dig att du placerar en boll på grafen. Bollen kommer att rulla nedåt (om du är över x-axeln, uppåt om du är under den) eftersom den söker sig till de punkter som ligger så nära x-axeln som möjligt. Här är en ytterst ful animation över hur det kan gå om du släpper bollen på fel ställe:

Edit: Nu funkar animationen också. :)

NR är en förkortning för Newton-Raphsons metod.

Om man startar sin NR-beräkning vid x=7, kommer man aldrig att komma förbi Smutstvätts puckel vid x=4,5 och hitta något nollställe.

Okej, jag förstår nu animeringen. Så för att hitta en rot till ekvationen som man söker måste gissningen vara tillräckligt nära roten man letar efter, precis som SeriousCephalopod skrev. 

Edit: Hur ska jag motivera det matematiskt? Kan man göra det med godtyckliga tal? 

SeriousCephalopod skrev:

Den är i princip garanterad att fungera så länge startgissningen är tillräckligt nära roten man letar efter.

Hur nära man måste vara beror på hur mycket funktionen varierar runt roten, om dess derivata eller värde oscillerar eller konvergerar mot något.

Men är du för långt bort vid startgissningen så kan du antingen landa i en annan rot en den den du sökte, fastna i en loop som inte konvergerar mot något, eller hamna i ett olösbart delsteg om man råkade pricka en punkt där $f'(x) = 0$ och därmed tangenten aldrig skär x-axeln. 

Vad menar du med hur mycket funktionen varierar runt roten, om dess derivata eller värde oscillerar eller konvergerar mot något? 

Hej!

Om du vill använda NR-metoden för att finna lösningen $x=\pi$ till ekvationen $\sin 2000 x = 0$ och startar i punkten $x_0 = \pi/3$ kommer du att misslyckas på grund av att sinusfunktionen är kraftigt oscillerande.

Jaha för att det är en sinusgraf. Jag antar att detsamma gäller för cossinus. Men varför spelar detta roll när vi vill kolla hur nära man måste vara? 

SeriousCephalopod skrev:

Den är i princip garanterad att fungera så länge startgissningen är tillräckligt nära roten man letar efter.

Hur nära man måste vara beror på hur mycket funktionen varierar runt roten, om dess derivata eller värde oscillerar eller konvergerar mot något.

Men är du för långt bort vid startgissningen så kan du antingen landa i en annan rot en den den du sökte, fastna i en loop som inte konvergerar mot något, eller hamna i ett olösbart delsteg om man råkade pricka en punkt där $f'(x) = 0$ och därmed tangenten aldrig skär x-axeln. 

 

Och en till fråga. Vad menar du med det fetstila?

Det med att f'(x) = 0 gör ju då att vi får nolldivision vilket ej är tillåtet. 

Wikipediaartikeln har beskrivningar av exempel med dåliga startpunkter

https://en.wikipedia.org/wiki/Newton%27s_method#Bad_starting_points

"Starting point enters a cycle" är fallet jag menar.

Tack för länken! 

Jag kollade in den och läste under rubriken Bad starting points.

Bad starting points
In some cases the conditions on the function that are necessary for convergence are satisfied, but the point chosen as the initial point is not in the interval where the method converges. This can happen, for example, if the function whose root is sought approaches zero asymptotically as x goes to ∞ or −∞. In such cases a different method, such as bisection, should be used to obtain a better estimate for the zero to use as an initial point.

Så det de menar är att om funktionen är konvergent, sammanhängande, men startvärdet är inte där metoden är konvergent. Vad menar de med att metoden är konvergent och sen med exemplet som de tagit upp? 

detrr skrev:

Tack för länken! 

Jag kollade in den och läste under rubriken Bad starting points.

Bad starting points
In some cases the conditions on the function that are necessary for convergence are satisfied, but the point chosen as the initial point is not in the interval where the method converges. This can happen, for example, if the function whose root is sought approaches zero asymptotically as x goes to ∞ or −∞. In such cases a different method, such as bisection, should be used to obtain a better estimate for the zero to use as an initial point.

Så det de menar är att om funktionen är konvergent, sammanhängande, men startvärdet är inte där metoden är konvergent. Vad menar de med att metoden är konvergent och sen med exemplet som de tagit upp? 

Att funktionen ska vara konvergent står ingenstans, och det begreppet saknar nog mening. Var står det sammanhängande?

Deras exempel säger att det finns funktioner som uppfyller alla krav för att metoden ska konvergera, t.ex. deriverbarhet (och att det finns en rot, och att funktionen är kontinuerlig), men att inte alla x-värden gör att metoden konvergerar, till exempel om funktionen närmar sig noll asymptotiskt när x växer.

detrr skrev:

Tack för länken! 

Jag kollade in den och läste under rubriken Bad starting points.

Bad starting points
...

Så det de menar är att om funktionen är konvergent, sammanhängande, men startvärdet är inte där metoden är konvergent. Vad menar de med att metoden är konvergent och sen med exemplet som de tagit upp? 

Ta en funktion som konvergerar mot 0 vid oändligheten såsom xe^(-x^2)

http://m.wolframalpha.com/input/?i=x+exp%28-x%5E2%29

Om du tar en startpunkt höger om högra puckeln så kommer iterationerna producera punkter som blir större och större. Processen "vandrar åt höger" utan att hitta nollstället i mitten och kommer aldrig till något nollställe alls. Därmed så säger vi att den inte konvergerar för sådana startpunkter.