Negera ett påstående

Negationen av "det existerar ett n sådant att P" är ekvivalent med "för alla n, ~P". Din första ekvivalens är alltså inte korrekt, utan det som står på andra raden är påståendet att "det finns ett naturligt tal som inte både är delbart med 5 och har sista siffra som inte är 0 eller 5". Ett sådant påstående är sant så länge det finns ett enda sådant tal. Till exempel är 7 ett sådant tal.

Det ekvivalenta påståendet ska istället vara "För varje naturligt tal n, så är n inte både delbart med 5 och har sista siffra som inte är 0 eller 5".

Enklaste sättet att negera ~P(n) är P(n).

Sedan kan det kanske vara bra att skriva om det, för att genomföra ett bevis.

Gustor skrev:

Negationen av "det existerar ett n sådant att P" är ekvivalent med "för alla n, ~P". Din första ekvivalens är alltså inte korrekt, utan det som står på andra raden är påståendet att "det finns ett naturligt tal som inte både är delbart med 5 och har sista siffra som inte är 0 eller 5". Ett sådant påstående är sant så länge det finns ett enda sådant tal. Till exempel är 7 ett sådant tal.

Det ekvivalenta påståendet ska istället vara "För varje naturligt tal n, så är n inte både delbart med 5 och har sista siffra som inte är 0 eller 5".

Det vi ska bevisa är dock ett påstående som redan har en negation (~). Eftersom vi negerar ett påstående som säger "det finns inte ett naturligt tal n som..." så borde det väl bli "det är inte så att det finns inte ett naturligt tal n som...", vilket blir "det finns ett naturligt tal n som..."?

Det blir alltså en dubbel negation, därför borde det väl vara rätt att det ska stå Ǝ. Eller tänker jag fel nu?

Laguna skrev:

Enklaste sättet att negera ~P(n) är P(n).

Sedan kan det kanske vara bra att skriva om det, för att genomföra ett bevis.

Det är det jag försökte göra, men enligt facit ska ju det inom det andra parentesparet vara oförändrat.

tahlas05 skrev:

Gustor skrev:

Negationen av "det existerar ett n sådant att P" är ekvivalent med "för alla n, ~P". Din första ekvivalens är alltså inte korrekt, utan det som står på andra raden är påståendet att "det finns ett naturligt tal som inte både är delbart med 5 och har sista siffra som inte är 0 eller 5". Ett sådant påstående är sant så länge det finns ett enda sådant tal. Till exempel är 7 ett sådant tal.

Det ekvivalenta påståendet ska istället vara "För varje naturligt tal n, så är n inte både delbart med 5 och har sista siffra som inte är 0 eller 5".

Det vi ska bevisa är dock ett påstående som redan har en negation (~). Eftersom vi negerar ett påstående som säger "det finns inte ett naturligt tal n som..." så borde det väl bli "det är inte så att det finns inte ett naturligt tal n som...", vilket blir "det finns ett naturligt tal n som..."?

Det blir alltså en dubbel negation, därför borde det väl vara rätt att det ska stå Ǝ. Eller tänker jag fel nu?

Det stämmer att negationen till ~(Ǝn:P) är Ǝn:P, men det är inte det du har skrivit.

Det jag säger är att negationen till ett påstående "det finns ett n sådant att P(n)" är "för alla n gäller ~P(n)". Alltså att ~(Ǝn:P) är ekvivalent med ∀n:~P.

Jag tror jag förstår vad som gått fel nu. Det ser ut som du har "distribuerat" negationen över de två parenteserna. Så kan man inte göra här eftersom de två parenteserna endast utgör ett påstående. Den första är bara en kvantifikator.

Gustor skrev:

Det stämmer att negationen till ~(Ǝn:P) är Ǝn:P, men det är inte det du har skrivit.

Det jag säger är att negationen till ett påstående "det finns ett n sådant att P(n)" är "för alla n gäller ~P(n)". Alltså att ~(Ǝn:P) är ekvivalent med ∀n:~P.

Jag tror jag förstår vad som gått fel nu. Det ser ut som du har "distribuerat" negationen över de två parenteserna. Så kan man inte göra här eftersom de två parenteserna endast utgör ett påstående. Den första är bara en kvantifikator

Jag förstår fortfarande inte riktigt varför jag inte ska distribuera negationen över de två parenteserna. Skulle du kunna förtydliga varför det inte är tillåtet?

När jag distribuerade negationen försökte jag följa det denna video säger mellan 2:49-4:10:
https://youtu.be/huGWXh4l1M0?si=7rBK3EkVwHFYhtOB&t=169

Negation kan man ta av ett påstående (formel). "Ǝn" är inte ett påstående i sig (det är formellt sett inte en giltig term eller formel i första ordningens logik). Jag skriver inte ut att n tillhör mängden naturliga tal, men samma gäller oavsett om man väljer att skriva ut det eller ej. Jämför med: "det existerar ett tal sådant att." Detta är inte ett påstående. Utan det är en möjlig del av ett påstående. Därför kan man inte heller ta negationen av det i sig, utan du måste ta negationen av hela påståendet.

Det som händer i videon är att man ska visa ett påstående på formen

∀n ~(P∧Q).

Enligt vad jag skrev tidigare så är ~∀n P ekvivalent med Ǝn ~P.

Negationen vi tar är alltså på hela formeln:

~(∀n ~(P∧Q)).

Även om det står två parenteser i uppgiften du frågade om, så finns det bara ett sätt att tolka denna formel, nämligen att negationstecknet i början gäller "hela" formeln/påståendet.

Vi får att ~(∀n ~(P∧Q)) är ekvivalent med Ǝn (P∧Q). Motsatsen till "för varje tal n gäller att n inte är både udda och jämnt" är alltså "det existerar ett tal som är både udda och jämnt". Vi distribuerar inte negationen utan vi använder oss av de ekvivalenser/regler som finns för negation av påståenden som börjar med en kvantifikator.

Bara för att förtydliga, är detta vad som sker eller har jag missuppfattat något: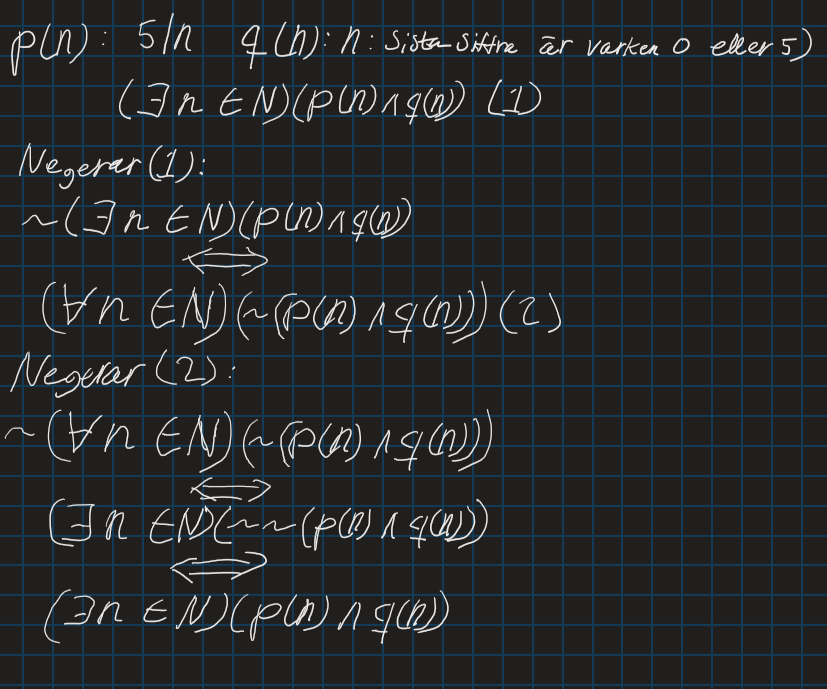

bump

Det ser helt korrekt ut det du skrivit, ja. Tar man negationen av något två gånger blir det ju alltid samma som man började med, men alla dina ekvivalenser är riktiga.

Gustor skrev:

Det ser helt korrekt ut det du skrivit, ja. Tar man negationen av något två gånger blir det ju alltid samma som man började med, men alla dina ekvivalenser är riktiga.

Tack!