När kan sinus strykas?
I ekvationerna sinx=sin3x och sin5x=sin4x, menar min mattebok att rätt svar ges av arcsin på båda sidor, dvs att sin "stryks". MEN med ekvationen sinx=sin2x ger samma metod fel svar. Att "stryka" sin på båda sidor ger x=360n och x= 60 + 120n. Svaret som efterfrågas är att utveckla sin2x till 2sinxcosx, flytta över sinx och faktorisera. Detta ger x=360n och x= 180 + 360n.
Så frågan är helt enkelt: när kan sin "strykas"? Krävs faktorisering endast för den sistnämnda ekvationen? Är den ett specialfall? Kan sin "strykas" för alla andra liknande ekvationer? Tack för svar!
Hej.
Det man gör med arcsin är inte att "stryka" sinus utan istället att man tar inversen av sinus på båda sidor. Det gäller då som alltid att komma ihåg att lägga till alternativvinkel plus periodicitet.
I det andra fallet, där ena vinkeln är dubbelt så stor som den andra, så är det praktiskt att använda formeln för dubbla vinkeln, faktorisering och nollproduktmetoden.
Men båda metoderna ger samma resultat.
Visa gärna hela din uträkning där du använder formeln för dubbla vinkeln, faktoriserar och använder nollproduktmetoden.
Hej. Jag är medveten om att det är inversen som används: "stryka"var mest ett praktiskt trivialnamn. Det jag inte förstod var varför det (till synes) inte fungerar att bara använda inversen i ekvationen sinx=sin2x. Jag bifogar bilder på mina lösningar nedan.
Här är en lösning som enligt facit är rätt. sin4x=sin5x. Marginalen visar vilka åtgärder som görs. (Inser att jag glömt skriva att 4x subtraheras efter steg 1.)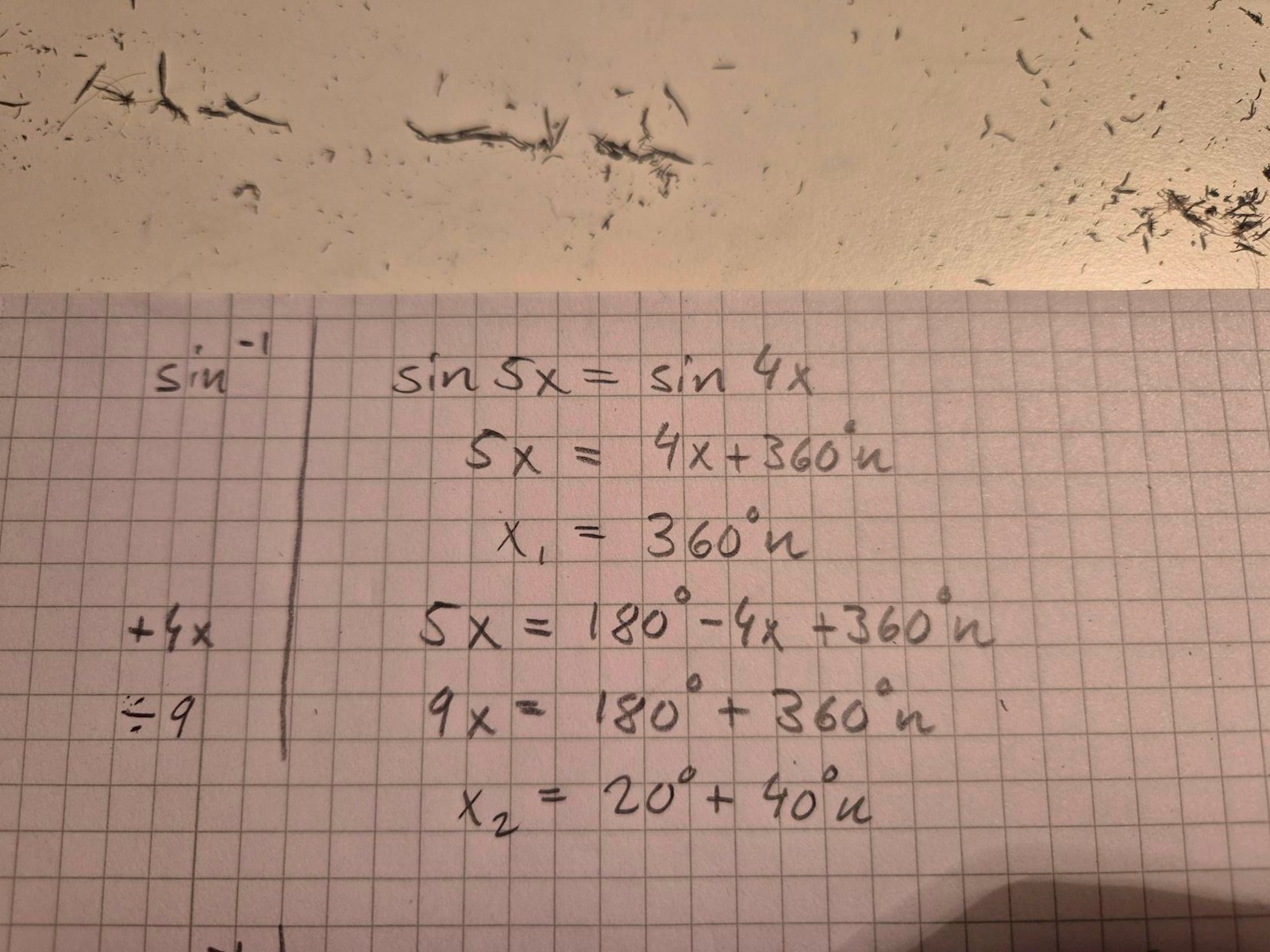
Nedan använder jag samma metod som i den förra ekvationen, men svaret blir inte helt rätt: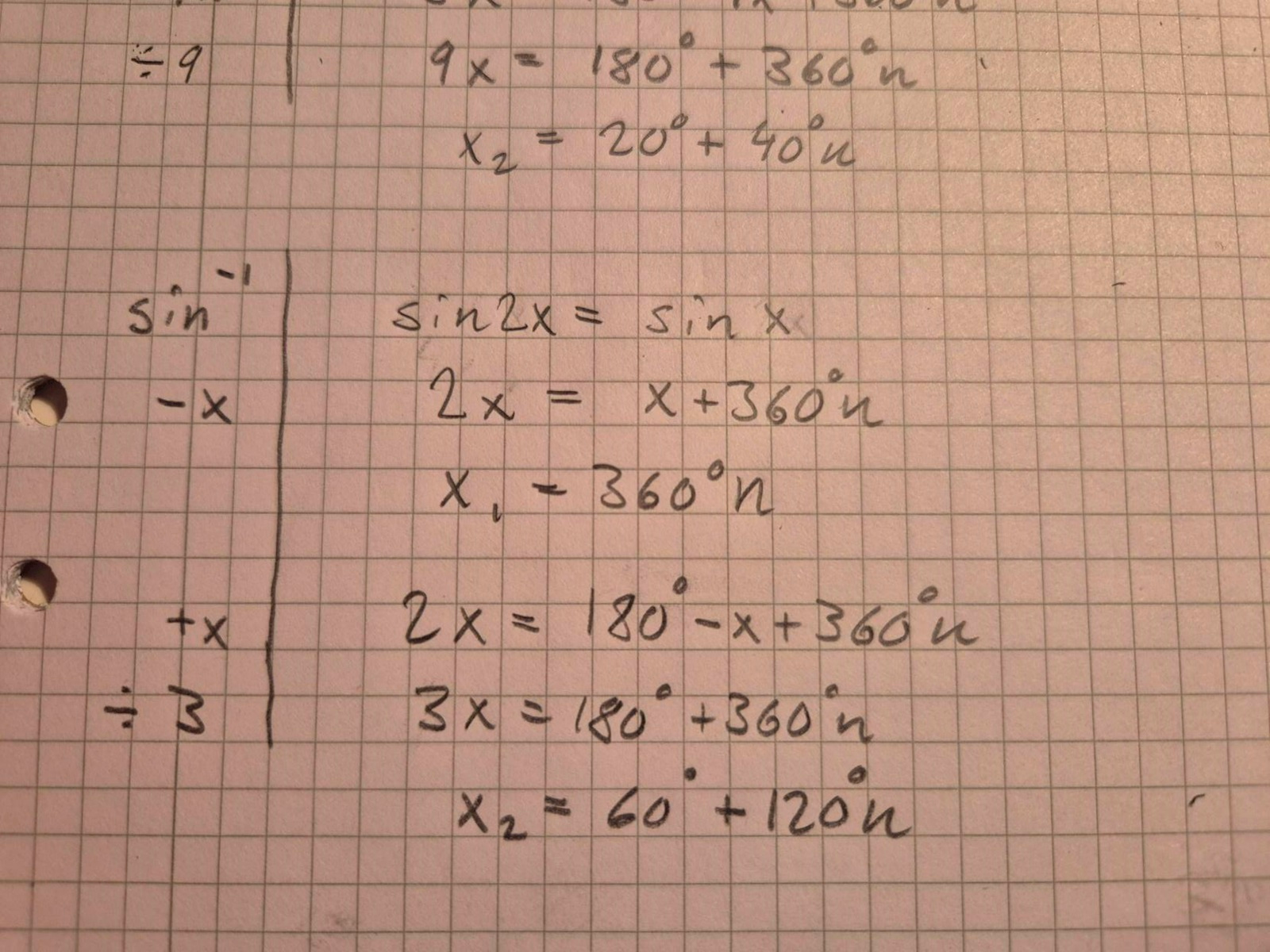
Än så länge ser allt bra ut. Klart och tydligt. Och rätt.
Här följer lösning med utveckling av sin2x och faktorisering, som ger det rätta svaret:
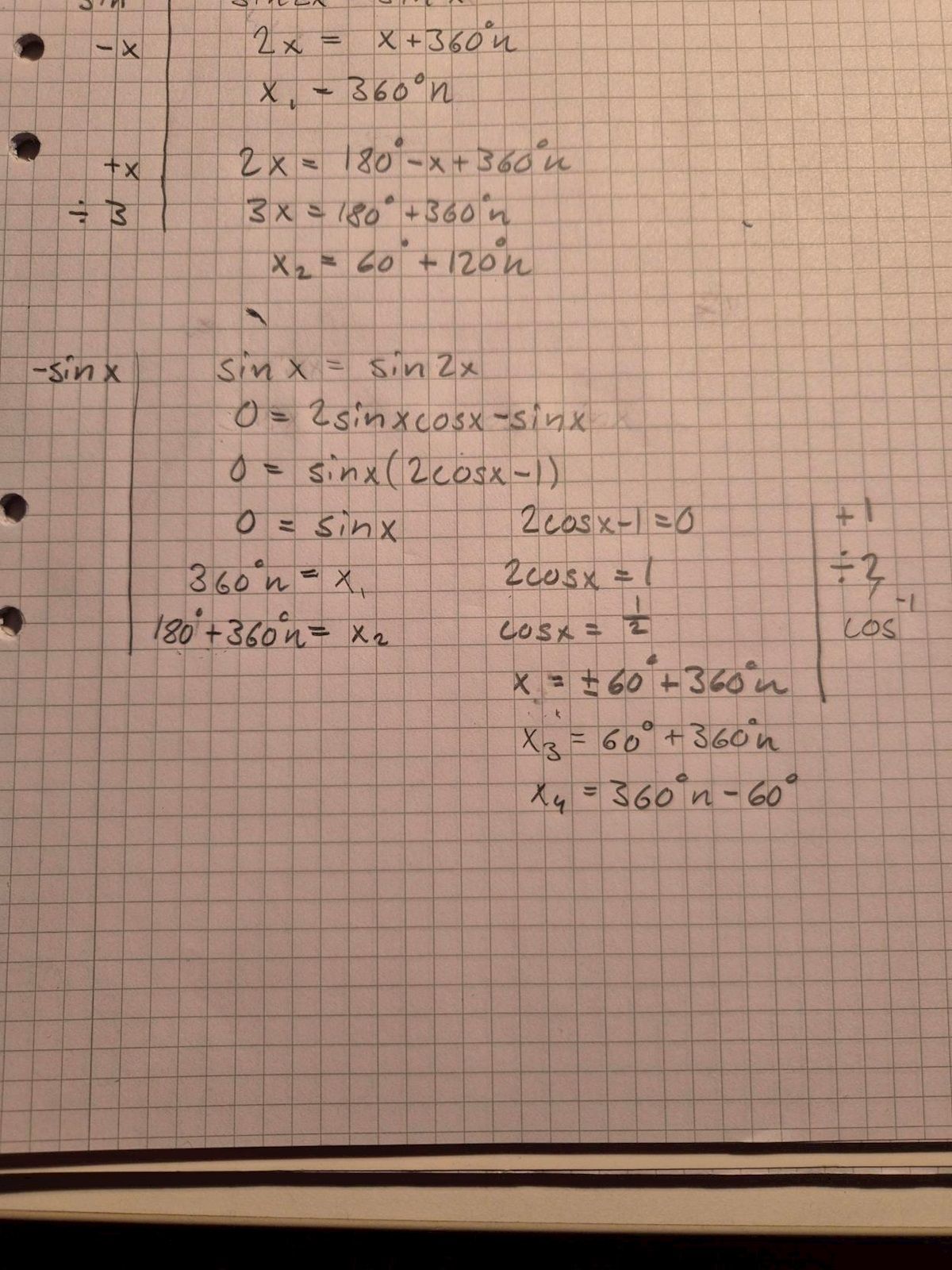
Även detta är helt rätt.
Skillnaden på de två sista lösningarna är att jag i den sista får både x=60 + 360n och x=360n - 60. Dessutom menade min lärare idag att det inte går att ta inversen till sinx=sin2x direkt, eftersom sin2x går att utveckla. Vilket gäller, egentligen?
Eckerström skrev:Skillnaden på de två sista lösningarna är att jag i den sista får både x=60 + 360n och x=360n - 60.
Lösningarna är identiska, vilket kanske inte ör så lätt att se direkt.
Men om du ritar två enhetscirklar och markerar den ena lösningsmängden i ena cirkeln och andra lösningsmängden i andra cirkeln så ser du nog att de sammanfaller?
Eckerström skrev:[...]
Dessutom menade min lärare idag att det inte går att ta inversen till sinx=sin2x direkt, eftersom sin2x går att utveckla. Vilket gäller, egentligen?
Der går utmärkt att använda inversen även där.
Läraren menade nog att det är elegantare/"böttre" att använda formeln för dubbla vinkeln.
Yngve skrev:Även detta är helt rätt.
Ritade upp en enhetscirkel. Nu klarnar det. Vad gäller läraren så missförstod vi antagligen varandra: jag uppfattade det som att inversen till den nämnda ekvationen gav fel svar. Men tack så mycket för hjälpen, ha en fin kväll!


