Når inte hela vägen fram i enkel matriskevation
Halloj!
Jag håller på att studera mycket enkla matrisekvationer och sitter just nu med följande uppgift:
Lös ekvationen om:
, ,
Jag började med att plocka fram inverserna till och genom att gaussa och kom då fram till:
,
Sedan tänkte jag att för att lösa ut ur matrisekvationen så blir det:
Men när jag försöker beräkna detta så får jag inte rätt svar. Har jag åtminstone rätt tänkt hittills, eller är det helt knasigt?
Jag tycker du har räknat rätt.
Och om vi gör kontrollräkningen
Ett misstag jag gjorde när jag försökte lösa uppgiften var att jag glömde att transponera i kontrollräkningen. Gjorde du något liknande?
Tillägg: 6 jan 2025 15:16
i den tredje matrisen i den första uträkningen ska vara positiv.
Hmm. Jag gjorde det i PAINT och har tyvärr inte sparat det, men jag misstänker att jag vet vad som kanske gick fel. I mina matriser och blev jag så irriterad på bråken att jag bröt ut 1/3 och 1/7. Sedan skrev jag om detta som en koefficient 1/21 framför multiplikationen av de tre matriserna. Kan det vara så att det inte går i matrismultiplikation?
Det går att bryta ut faktorer, om du bryter ut dem från alla positioner
Det var det jag gjorde, så det är märkligt att svaret inte blev samma då. Jag tänkte så här:
Är det okej så långt? Det känns som att felet har något att göra med att denna typ av multiplikation inte är kommutativ.
naytte skrev:Det var det jag gjorde, så det är märkligt att svaret inte blev samma då. Jag tänkte så här:
Är det okej så långt? Det känns som att felet har något att göra med att denna typ av multiplikation inte är kommutativ.
ska vara positiv i den tredje matrisen! Jag skrev detta fel i min LaTeX i mitt svar så om du kollade på det svaret så var det mitt misstag!! Men om man rättar det så blir den där beräkningen du skrev rätt.
Så, rättat. Jag kopierade din LaTeX-kod rakt av utan att titta ordentligt, men så som det står nu vad så jag räknade.
Hur ska man tänka kring ordning här, då? Jag vet att matrismultiplikation är associativ så kan jag börja med de två matriserna längst till höger, sedan multiplicera produkten med matrisen längst till vänster, och sedan multiplicera allt med 1/21?
Nu blev det rätt. Måste ha räknat fel igår...
Tack för hjälpen!
naytte skrev:Hur ska man tänka kring ordning här, då? Jag vet att matrismultiplikation är associativ så kan jag börja med de två matriserna längst till höger, sedan multiplicera produkten med matrisen längst till vänster, och sedan multiplicera allt med 1/21?
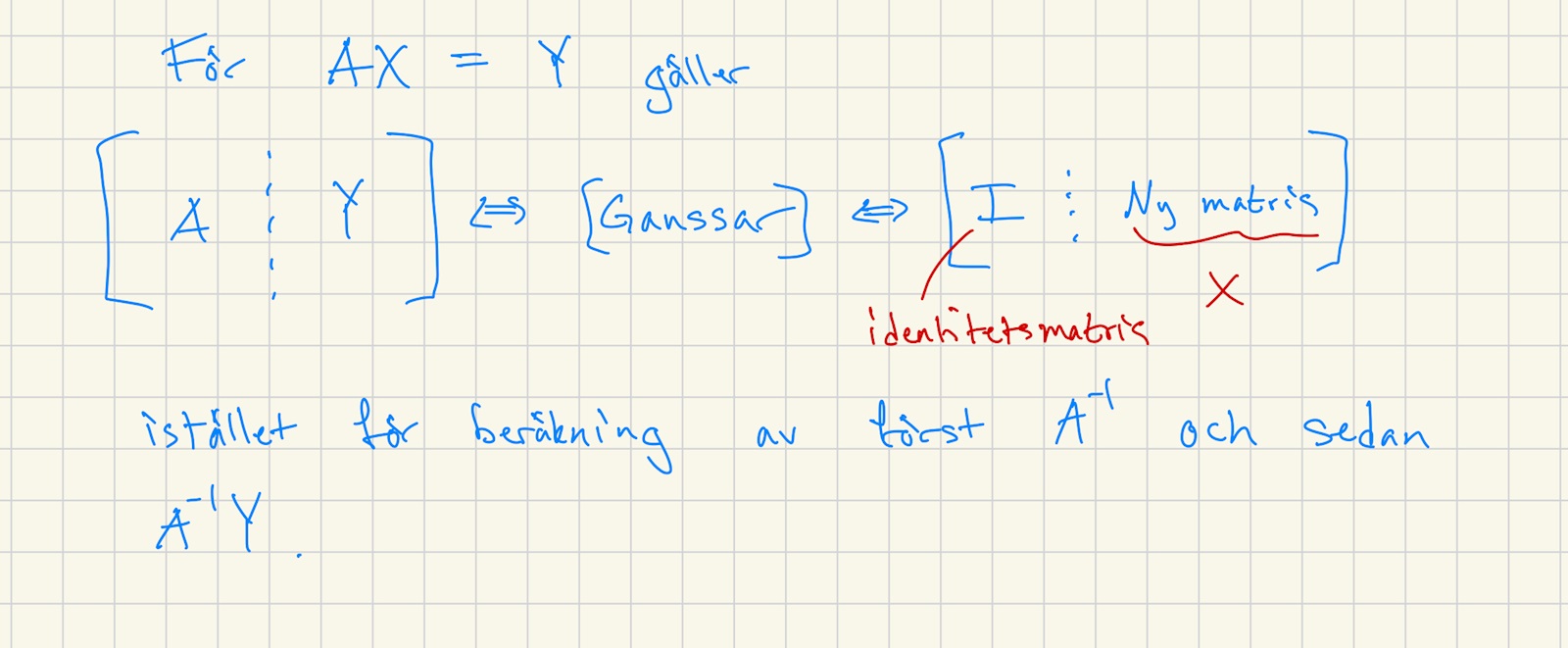
Ja, det går. Ett annat lättare sätt är att skriva om den på formen
AX=C(BT)-1
och sedan löst den i ett enda gauss-steg som du gör för en ekvation på formen AX=Y.
och sedan löst den i ett enda gauss-steg som du gör för en ekvation på formen AX=Y.
Skulle du kunna visa hur du menar? Jag har bara sett det göras då X och Y är kolonnmatriser.
Jaha, så menar du. Men jag förstår inte direkt hur detta är lättare än att bara göra som jag gjorde. Här måste man väl ändå beräkna produkten C(BT)-1?
Ja, men du slipper ju att både beräkna A invers och produkten av A-1 och Y. Beroende på uppgift kan att beräkna dessa vara väldigt jobbigt, ibland knappt lösligt.