När har funktionen extrempunkter
Hej! Jag har problem med att lösa denna uppgift. 
Jag har löst a, men vet inte hur jag ska lösa b och c. Här är min lösning: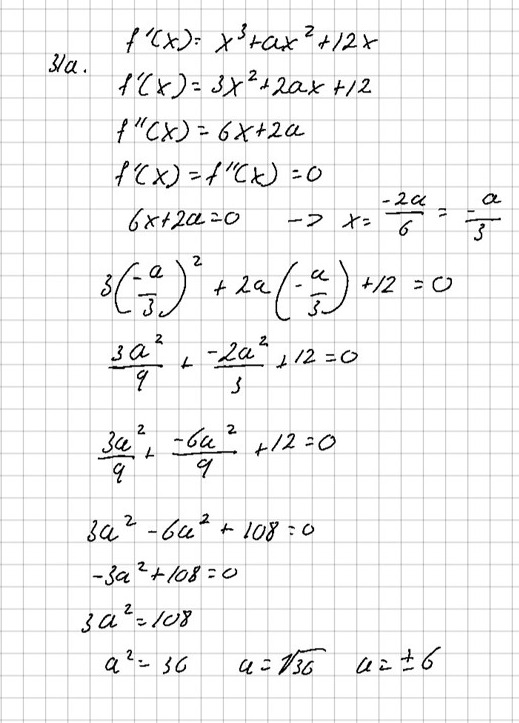
Jag vet att för två nollställen måste f'(x)=0 och ha två rötter, men vet inte hur jag ska räkna ut.
Det är en bra början. Men nu måste du dessutom undersöka om dessa värden på verkligen ger terasspunkter eller inte. Bara för att måste det inte vara en terasspunkt. Det kan vara en minimipunkt också som hos . Där blir , trots att det inte är en terasspunkt.
För b-uppgiften:
Det stämmer att evkationen ska ha två lösningar. Eftersom är en andragradskurva kanske du kan dra nytta av pq-formeln eller abc-formeln? Fanns det inte något krav med diskriminanten för att det skulle finnas två lösningar...? ;)
Jag la in a=+-6 i f'(x)=0 och löste att terrasspunkterna kan finnas vid x=2 och x=-2, jag testade sedan lutningen ett tal mindre och ett tal mer och de hade positiv luting på båda sidorna.
jag är inte säker på hur jag ska lösa b eller c, man måste dessutom lösa uppgiften utan digitala verktyg, så jag kan inte ens rita en graf :(
En graf behöver du inte!
Börja med att derivera funktionen så får du .
Kommer du ihåg hur pq-formeln ur ma2 ser ut?
jag försökte, men kunde inte lista ut hur man löser a utifrån det.
jag fick fram att x1=-2, x2=
Hur ser diskriminanten för pq-formeln ut?

detta är vad jag fick det till
Din förenkling stämmer inte men diskriminanten verkar vara rätt uppställd!
Vad måste gälla för diskriminanten för att det ska finnas två reella lösningar?
Hur många finns det om diskriminanten är mindre än 0, och hur många finns det när den är 0?
diskriminaten måste inte bli 0. Jag försökte lösa och sedan skulle svaret då vara < eller > än det jag fick fram, jag satte då x värderna x=-2 och x=2 eftersom det är då lutningen blir 0, men jag fick då fram att a>3 ller a<-6, som inte stämmer med facit
Diskriminanten måste vara >0. Då finns det två reella lösningar. För vilka a blir diskriminanten större än 0?
jag får det fortfarande till 3?
Oj, jag var lite ouppmärksam. Du ska inte sätta in 2ax i diskriminanten, bara 2a.
då blir svaret rätt, men vart försvinner x:et då?
pq-form är ju x2+px+q. p i det här fallet blir ju 2a, det vill säga det du ska stoppa in i pq-formeln.
Ah just det...
Missade att ta bort x:et i min lösning.
Då får jag rätt svar, tack så mycket :)


