Några personer skakar hand med varandra - Dirichlets lådprincip
Hej!
Jag skulle behöva hjälp med följande uppgift: Visa att om ett antal personer träffas och skakar hand med varandra på måfå, så måste det hela tiden finnas minst två personer som har skakat hand med lika många personer.
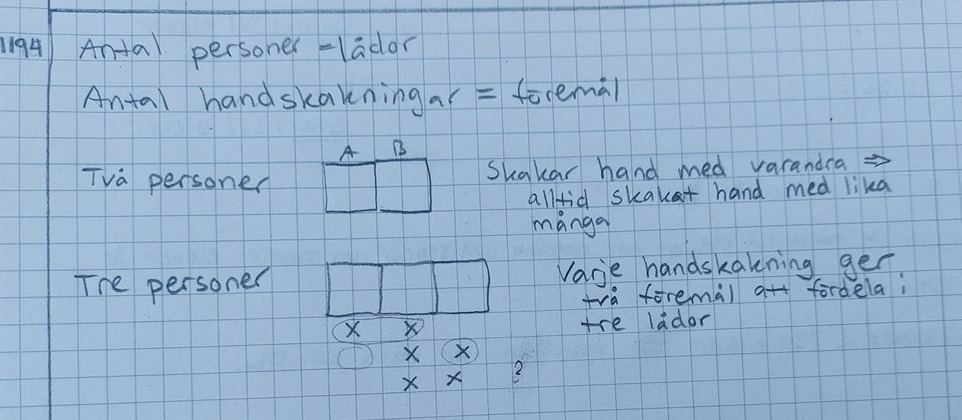
Jag tänker att antal personer är lådor och antal handskakningar är föremål. Min första tanke är att jag ska göra en falluppdelning, men det blir problem redan vid tre personer.
Det känns inte som att det här är rätt tillvägagångssätt.
Tack på förhand
Eftersom du vill visa att det finns minst två personer som skakat hand med lika många personer kan det matcha bra med lådprincipen om en låda är ”har skakat hand med k personer”. Om du då kan komma fram till (med lådprincipen) att det finns minst en låda med minst två personer i är du klar.
Tack så mycket!
Ser mitt resonemang här bättre ut och är det tillräckligt?
m är antalet personer/föremål
n är antalet personer en person har skakat hand med/lådor
Man kan aldrig skaka hand med sig själv och därför är m>n
Enligt Dirichlets lådprincip: Om m föremål fördelas i n lådor och m>n så måste någon låda innehålla minst två föremål. Detta innebär här att det alltid finns minst två personer som har skakat hand med lika många personer
Ja, om alla skakar hand med minst en annan person (och det är kanske så uppgiften är tänkt).
Om man även tillåter att någon inte skakar hand med någon annan så fungerar ett liknande resonemang, för om minst en person inte skakar hand med någon annan så kan ingen skaka hand med alla andra. I det fallet är n < m-1 och det blir också m-1 lådor (0 till m-2 att skaka hand med) och m personer att placera i de m-1 lådorna så minst en låda med två personer.
Det måste finnas en begränsning att två personer inte får skaka hand med varandra flera gånger.
Yngve skrev:Det måste finnas en begränsning att två personer inte får skaka hand med varandra flera gånger.
Tack
Så för att mitt resonemang ska fungera måste det finnas en begränsning att man inte får skaka hand med samma person igen?
Är det några ändringar i resonemanget om begränsningen inte finns?
linsun06 skrev:
Tack
Så för att mitt resonemang ska fungera måste det finnas en begränsning att man inte får skaka hand med samma person igen?
Är det några ändringar i resonemanget om begränsningen inte finns?
Glöm det jag skrev.
Jag tänkte att om två personer skakar hand med varandra två gånger så räknas det som två handskakningar var.
I så fall skulle tre personer A, B och C kunna ha 3, 2 respektive 1 handskakningar (A+B, A+B igen, A+C).
Men nu när jag läser uppgiften mer noga så ser jag att det står att det alltid finns minst två personer som har skakat hand med lika många personer. Då räknas dubbelskakningar ändå bara som att man har skakat med en person och våra A, B och C skulle då ha 2, 1 och 1 skakningar.
Okej, tack.
Så mitt resonemang är tillräckligt utförligt för att lösa uppgiften?
Jag tycker du inte att ditt resonemang fungerar och jag tror inte att detta går att lösa enbart med lådprincipen.
Problemet är att du verkar tänka att det finns fler personer än lådor, men det gör det inte.
Låt oss som exempel anta att det finns 25 personer. Då finns det också 25 lådor, för varje person kan ha skakat hand med allt mellan 0 och 24 personer, det vill säga det finns 25 lådor.
Så endast utifrån lådprincipen löser vi inte detta.
Men: är det verkligen möjligt att en person A skakat hand med alla andra samtidigt som en annan person B inte skakat hand med någon? Det vill säga: är det verkligen möjligt att en person är låda 0 samtidigt som en annan är i låda 24 ( i exmeplet med 25 personer)?
Smutsmunnen skrev:Jag tycker du inte att ditt resonemang fungerar och jag tror inte att detta går att lösa enbart med lådprincipen.
Problemet är att du verkar tänka att det finns fler personer än lådor, men det gör det inte.
Låt oss som exempel anta att det finns 25 personer. Då finns det också 25 lådor, för varje person kan ha skakat hand med allt mellan 0 och 24 personer, det vill säga det finns 25 lådor.
Så endast utifrån lådprincipen löser vi inte detta.
Men: är det verkligen möjligt att en person A skakat hand med alla andra samtidigt som en annan person B inte skakat hand med någon? Det vill säga: är det verkligen möjligt att en person är låda 0 samtidigt som en annan är i låda 24 ( i exmeplet med 25 personer)?
Tack!
Rent logiskt tänker jag att det inte är möjligt att person A har skakat hand med alla samtidigt som person B inte har skakat hand med någon. Jag antar att det behövs något matematiskt resonemang, men jag har fastnat helt.
Inte svårare än så här: om A har skakat hand med alla så har A skakat hand med B och då kan B inte ha skakat hand med ingen.
Okej, tack!
Så det resonemanget är isåfall tillräckligt?
Tack så mycket för all hjälp!


