något tal som ger neg lutning
om man har
3 e0,3x
finns det något x-värde som ger att lutningen är negativ?
Visa spoiler
svaret är nej, men fattar inte hur och varför?
är det att svaret inte kan bli negativt? (oavsett vilket x man har?)
men sedan finns en annan fråga
"För vilka x-värden är f avtagande om..
a) f(x) = x - ex b) f(x) = x + ex
Visa spoiler
på a frågan är svaret x > 0 och på b frågan är svaret f växer för alla x.
tycker dessa två frågor är rätt lika, men fattar inte hur man kommer fram till svaren?
naturnatur1 skrev:om man har
3 e0,3x
finns det något x-värde som ger att lutningen är negativ?
Visa spoiler
svaret är nej, men fattar inte hur och varför?
är det att svaret inte kan bli negativt? (oavsett vilket x man har?)
Lutningen kan inte bli negativ. Derivera och undersök om något x kan ge en negativ derivata (avtagande funktion).
Sedan kan du generellt fundera på exponentialfunktioner Ca^kx. Hur påverkar konstanterna C, a och k funktionen? Rita gärna grafer och fundera!
men sedan finns en annan fråga
"För vilka x-värden är f avtagande om..
a) f(x) = x - ex b) f(x) = x + ex
Visa spoiler
på a frågan är svaret x > 0 och på b frågan är svaret f växer för alla x.
tycker dessa två frågor är rätt lika, men fattar inte hur man kommer fram till svaren?
Eftersom det handlar om lutningen så rekommenderar jag att derivera och undersöka derivatans tecken istället.
mrpotatohead skrev:
men sedan finns en annan fråga
"För vilka x-värden är f avtagande om..
a) f(x) = x - ex b) f(x) = x + ex
Visa spoiler
på a frågan är svaret x > 0 och på b frågan är svaret f växer för alla x.
tycker dessa två frågor är rätt lika, men fattar inte hur man kommer fram till svaren?
Eftersom det handlar om lutningen så rekommenderar jag att derivera och undersöka derivatans tecken istället.
tack för svar
när jag deriverar så får jag på a frågan
x - ex = 0
1 - ex = 0
1 = ex
ln(1) = x
men förstår inte riktigt hur jag ska ta mig vidare?
samma gäller b frågan
x + ex = 0
1 + ex = 0
ex = -1
vilket inte funkar? (då dras nog slutsatsen att det inte finns x-värden där f avtar?)
Jag har inte kollat på resten, men på a)-delen blir det väldigt konstigt. Det du har är att f(x)=x-ex, inte att x-ex=0.
naytte skrev:Jag har inte kollat på resten, men på a)-delen blir det väldigt konstigt. Det du har är att f(x)=x-ex, inte att x-ex=0.
ja, det var nog fel att skriva = 0.
hade varit bättre om jag skrev
f(x) = x - ex
f'(x) = 1 - ex
men hur fortsätter jag min lösning? jag vill ju ha ut vilka x som är avtagande, och här och nu vet jag inte riktigt hur jag ska fortsätta med lösningen efter deriveringen?
I första fallet är derivatan 1 - ex, vilket blir negativt när ex > 1, alltså när x > 0. I det andra fallet är derivatan strikt positiv.
MangeRingh skrev:I första fallet är derivatan 1 - ex, vilket blir negativt när ex > 1, alltså när x > 0. I det andra fallet är derivatan strikt positiv.
hur kom du fram till det? förstår tanken bakom det (då ex alltid blir positivt kommer x större än 0 ge ut tal större 1. --> 1 - tal större än 1 --> negativa svar)
men hur redovisar man det som lösning?
Jag tycker att lösningen står i mitt svar: för a) x > 0 (för större x blir derivatan negativ) för b) finns inga x som ger avtagande lösning (derivatan är positiv för alla x).
Lös olikheten f'(x)<0 så får du ett intervall där f(x) är avtagande.
ja, jag kollade upp lösningsförslag också och det blev såhär
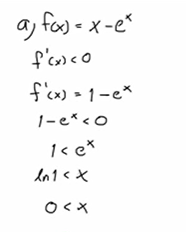
och är med på banan nu, tack till er alla i tråden.



