N(T) & R(T) komplexa matriser

Jag behöver hjälp med denna uppgift. Jag har svårt att förstå själva matrisen och hur den ser ut.
Hur kan man skriva om matrisen så att den ser ut så här; 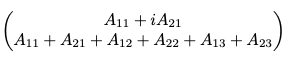
Låt A vara en godtycklig matris, dvs med elementen Aij för i∈{1,2} och j∈{1,3}.
Utför multiplikationen i matrisen T för att lösa ut elementen.
Calle_K skrev:Låt A vara en godtycklig matris, dvs med elementen Aij för i∈{1,2} och j∈{1,3}.
Utför multiplikationen i matrisen T för att lösa ut elementen.
jag förstår forfarande inte hur man gör det skulle du kunna visa steg för steg?
är A=(A11A12A13A21A22A23)

så
nu har jag förstått matrisen. Hur bestämmer jag N(T)?
Vad är definitionen av N(T)?
Det är mängden av lösningar till den homogena ekvationen A x = 0

dvs
ska jag använda mig av standardbaser? för just nu hhar jag en allmän matris
Nja, N(T) är de matriser A sådana att T(A)=0.
Det är bara att ställa upp som ett ekvationssystem och lösa.
hur löser man ekvationen
jag får
(A11+iA21A21+A12+A22+A13+A23-iA21)
Det där är ingen ekvation.
Sätt det lika med 0.
Sedan är det ett vanligt linjärt ekvationssystem, bara med ovanligt många fria variabler.
menar du så,
A11=-iA21A12=iA21-A21-A22-A13-A23
Ja visst.
hur gör jag sen?
när jag sätter in basmatrisen får jag
(100000)=(11),
har jag tänkt rätt??
Du bör ta för vana kolla dina svar själv.
Först kan du kolla om de matriser du fått fram avbildas på nollvektorn i C2. Om inte, får du räkna om.
Sedan kan du lista ut om du fått ut rätt antal matriser. Har nollrummet dimensionen 4?
ska jag ställa upp dem i en matris, så här?
Nja, det räcker väl att kolla att T(A) = , där A kan vara vilken som helst av de matriser som du fick fram.
I princip räcker det att kolla att A11 + iA21 = 0 samt att alla element i matrisen summerar till noll.
hur undersöker jag om de matriser jag fått fram avbildas på nollvektorn i C^2?
har jag fått fram rätt matriser?
Använd definitionen av T som ges i problemet för att kolla att T(A) = , då A är var och en av de matriser som du fått fram.
I så fall ligger matriserna i N(T). Du har redan noterat att de är linjärt oberoende. Om de spänner upp hela N(T) så är de en bas för N(T). Spänner de upp hela N(T)?
Ett sätt att visa att de måste vara en bas är att räkna ut dimensionen på N(T). Om dim(N(T)) = 4 så måste matriserna utgöra en bas för N(T), eftersom varje uppsättning om 4 linjärt oberoende vektorer i ett fyrdimensionellt vektorrum är en bas för vektorrummet. Är dim(N(T)) = 4?
såhär?
jag kollar att
Detta innebär att mina matriser ligger i N(T).
PÅvisar då detta att dim(N(T))=4 då vi har fått fyra oberoende matriser?
då kan vi använda oss av dimensionsformen och får att, 6=dim(N(T))+dim(R(T)) --> dim(R(T))=6-4=2



