Mysig trippelintegral

Börja med att rita upp området.  Lägg upp bilden här. 

Tänk på att du kan separera dessa som ett snitt:

$1 + z \geq |x| \land |y| \leq 1-z$

Sedan kan du om du har $1+z \geq |x|$ som vanligt formulera att $1+z\geq x\geq -(1+z)$.

Tillägg: 27 maj 2022 11:31

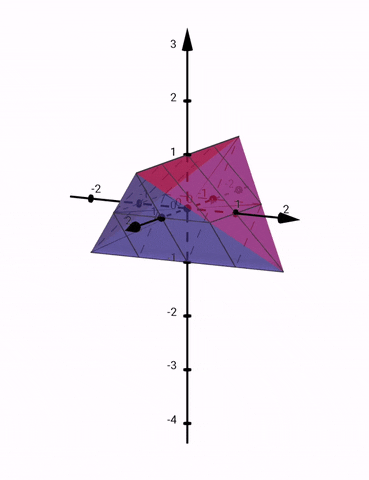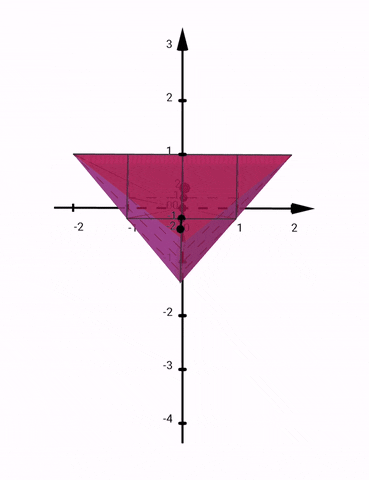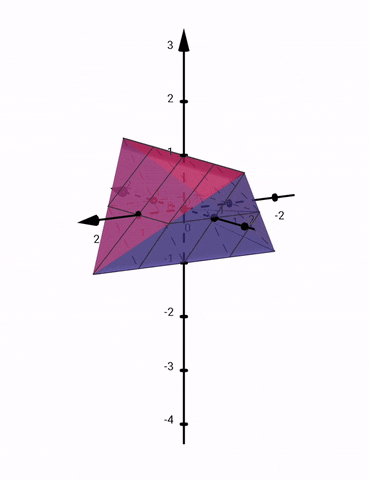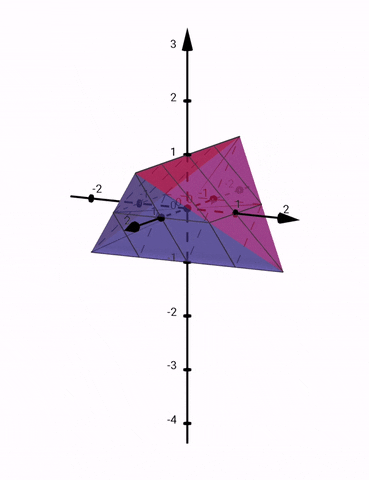
Detta är en illustration av området:

SaintVenant skrev:

Tänk på att du kan separera dessa som ett snitt:

$1 + z \geq |x| \land |y| \leq 1-z$

Sedan kan du om du har $1+z \geq |x|$ som vanligt formulera att $1+z\geq x\geq -(1+z)$.

---

Tillägg: 27 maj 2022 11:31

Detta är en illustration av området:

Riktigt fin bild. 

Så utifrån $$\begin{gathered} \left|x\right|-1\le z\le 1-\left|y\right| \\ ser vi att: \\ -1\le z\le 1 \\ 1+z\ge x\ge -(1+z) \\ 1-z\ge y\ge -(1-z) \end{gathered}$$

Är det bara att stoppa in dessa tre i en trippelintegral o tuta o köra?

Ser bra ut.

pepsi1968 skrev:

SaintVenant skrev:

Tänk på att du kan separera dessa som ett snitt:

$1 + z \geq |x| \land |y| \leq 1-z$

Sedan kan du om du har $1+z \geq |x|$ som vanligt formulera att $1+z\geq x\geq -(1+z)$.

---

Tillägg: 27 maj 2022 11:31

Detta är en illustration av området:

Riktigt fin bild. 

 

Så utifrån $$\begin{gathered} \left|x\right|-1\le z\le 1-\left|y\right| \\ ser vi att: \\ -1\le z\le 1 \\ 1+z\ge x\ge -(1+z) \\ 1-z\ge y\ge -(1-z) \end{gathered}$$

 

Är det bara att stoppa in dessa tre i en trippelintegral o tuta o köra?

Hur är det du grafar dem så snyggt?

Geogebra 3D för Android.