Multiplicera två icke realla faktorer
Hej jag förstår inte hur man ska utföra denna multiplikationen:
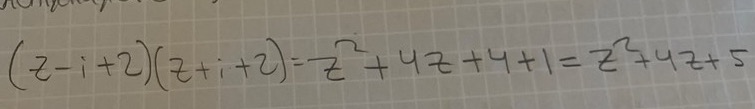
svaret är från att ja kolla facit för att försöka förstå och som jag tror de har gjort är att ta alla termerna upphöjt till två ( alltså Z2, 22=4, i2=-1) men då förstår jag inte vart 4Z kommer ifrån. Jag antar att det är 2*2*Z. Men varför tar man inte med i? Och varför tar man ens med den här termen över huvud taget. Och varför är det inte -4? Det är ju typ konjugat regeln så då ska det vara a2-b2? Ja antar att de andra teckens som har blivit plus är pga i2=-1 men de ska väl inte vara med i det andra termerna eller? Jag förstår inte hur multiplikationen har gått till…?
Om uttrycket hade varit (z-(i+2))(z+(i+2)) så hade du kunnat använda konjugatregeln och då fått z2-(i+2)2. Men nu är det inte så.
===
Pröva istället att multiplicera ihop alla termer enligt följande räkneschema:
(a+b+c)(d+e+f) = ad+ae+af+bd+be+bf+cd+ce+cf
Vad får du då?
Och kan du sedan förenkla detta uttryck något?
Yngve skrev:Om uttrycket hade varit (z-(i+2))(z+(i+2)) så hade du kunnat använda konjugatregeln och då fått z2-(i+2)2. Men nu är det inte så.
===
Pröva istället att multiplicera ihop alla termer enligt följande räkneschema:
(a+b+c)(d+e+f) = ad+ae+af+bd+be+bf+cd+ce+cf
Vad får du då?
Och kan du sedan förenkla detta uttryck något?
Ahhhh nu förstår jag. Jag gjorde så där först men det måste blivit något fel i förenklingen för jag hade ”i” kvar i mitt färdiga svar. Men nu fick ja bort alla dem!! Tack så mycket! Jag blev förvirrad av att jag gjorde fel och att facit gick direkt till svaret då ja tänkte om de fanns nån formel/strategi jag inte visste om/tänkte på…!
Yngve skrev:Om uttrycket hade varit (z-(i+2))(z+(i+2)) så hade du kunnat använda konjugatregeln och då fått z2-(i+2)2. Men nu är det inte så.
men man kan skriva det som
((z+2)-i)((z+2)+i) konjugatregeln ger
(z+2)2-i2
som kan utveckla med kvadreringsregeln till
z2+4+4z+1 =
z2+4z+5 =



