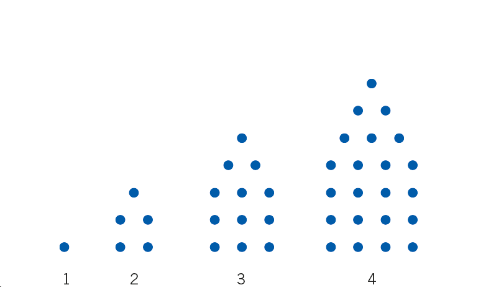
Mönster: antal punkter i figur N
Mönstret fortsätter på samma sätt som figuren visar.
a) Hur många punkter finns det i figur nr 10?
Min beräkning hittills var att separera det till två uttryck, dvs N^N för att hitta arean av kvadraten sedan räknar jag bara ut hur många extra prickar som adderas på det.
så i detta fall lägger jag det i en tabell där vänster sida är figuren och högra är antalet prickar som adderas på kvadraten
| 1 | 0 |
| 2 | 1 |
| 3 | 3 |
| 4 | 6 |
men jag kommer ingen vart med denna informationen allt jag vet att n^n plus vad figur n blir för tabellen kanske blir svaret.
Om nån som är kunnig skulle vara snäll och förklara vad man ska göra samt ge svar skulle vara snällt.
c) Finn ett uttryck för antalet punkter i figur nr n
Antal punkter i figur nr n=
För att se ett mönster behöver du också hur många prickar som finns i varje figur. Att jämföra detta med figurens nummer brukar oftast vara tillräckligt för att se ett mönster.
Jag tänker så här kvadraten i botten har n2 punkter.
triangeln som är kvar har 1+2+3+4+…+(n–1) punkter.
Sedan måste man veta (eller härleda) att 1+2+3+…+ M = M(M+1)/2
Marilyn skrev:Jag tänker så här kvadraten i botten har n2 punkter.
triangeln som är kvar har 1+2+3+4+…+(n–1) punkter.
Sedan måste man veta (eller härleda) att 1+2+3+…+ M = M(M+1)/2
jag har tänkt efter men jag kom fram till n(n-1)/2
hur kunde du veta att det var +1 istället?
Du gör rätt. Du summerar ju 1+…+(n–1)
Min formel summerar 1+…+M
Marilyn skrev:Du gör rätt. Du summerar ju 1+…+(n–1)
Min formel summerar 1+…+M
så nu har jag kommit fram till att (n-1)*n är samma som n^2-n och att (n^2-n) kommer att vara kvadratens area men hur skulle man då räkna triangelns? gör man då n*(n-1) altså (n^2-n)/2?
Jag förstår inte.
Kvadratens antal punkter är n2 som är = 2n2 /2
Triangeln har (n2–n)/2 punkter.
lägg ihop:
2n2 / 2 + (n2–n) / 2 = (2n2 + n2 – n) / 2 = (3n2 – n) / 2
För figur 10 som har en kvadrat med 100 pkter och en triangel med 45 pkter ger uttrycket
(300–10)/2 = 145, stämmer.
Marilyn skrev:Jag förstår inte.
Kvadratens antal punkter är n2 som är = 2n2 /2
Triangeln har (n2–n)/2 punkter.
lägg ihop:
2n2 / 2 + (n2–n) / 2 = (2n2 + n2 – n) / 2 = (3n2 – n) / 2
För figur 10 som har en kvadrat med 100 pkter och en triangel med 45 pkter ger uttrycket
(300–10)/2 = 145, stämmer.
Yes tack så mycket för hjälpen jag kom fram till sammar svar efter att ha spenderat två timmar på denna uppgift, jag tänkte att n^2-2n+(n^2-n)/2 skulle bli svaret om man skullle föränkla det till (2n^2-2n+n^2-n)/2
vilket blir samma som din!
Tackar för hjälpen och för din tid!
Du skriver n^2-2n+(n^2-n)/2
andra termen –2n vill jag inte ha med.
Jag tror du tänker att den undre figuren har bredd n och höjd (n–1).
I så fall blit triangeln litet större och du får
[n^2-2n+(n^2+n)]/2
och då har vi samma svar.
Slutet gott allting gott!


