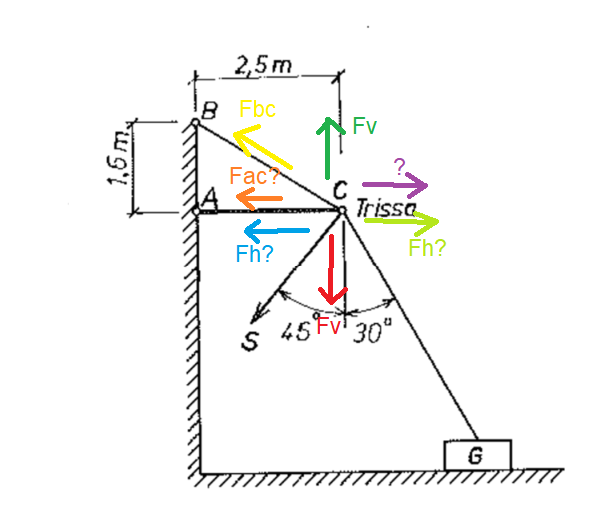
Moment med last och stag
Är ett tag sen jag höll på med fysik så tänket har somnat in en aning märker jag.
Har en uppgift här där man ska beräkna spänning i ett horisontellt stag som är fäst i ett rep mot en vägg och där en last hänger i dess yttre ände.
Repet (S) dras med en kraft på 0,45 kN, men rubbar inte lasten G på marken.
Man söker alltså hur mycket spänning det blir på AC respektive BC, där egentyngderna i detta fall försummas.
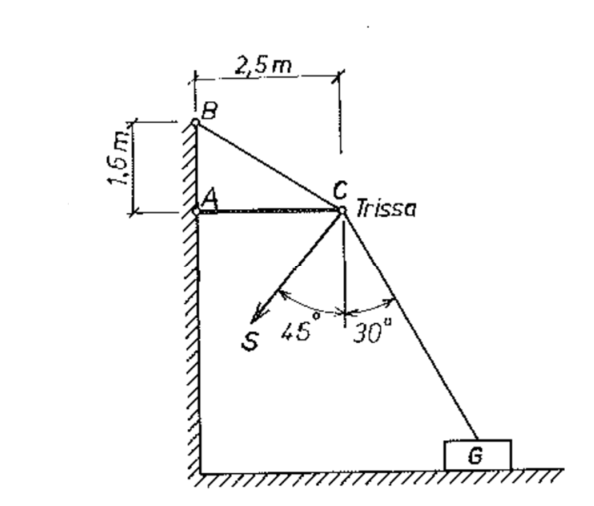
Så jag började med att försöka ta reda på hur stor kraften blir nedåt, eftersom det då lär vara lika stor kraft uppåt i de båda stagen.
Repet S dras med 0,45 kN, men föremålet G rubbas inte, alltså jämvikt, då tänker jag att repet till G drar emot med en kraft på (minst) 0,45 kN.
Tog fram x och y komposanter på respektive rep för att med pythagoras sats ta fram resultantkraften som staget utsätts för.
Fick då 0,72 kN, med Fx = -0,09 kN och Fy = -0,71 kN
Tog även arctan Fy/Fx vilket gav vinkeln 82,8 gr som resultanten riktar sig mot. Skulle anta att det rör sig om neråt vänster, men är inte helt hundra på detta och vilken exakt riktning den hamnar.
Sen kommer ju riktningen att påverka hur det horisontella staget angrips, då momentet där påverkas av att angreppet inte är helt rätvinkligt.
Är även osäker på hur jag tar mig vidare för att fördela kraften för momentet på staget AC, och snöret BC som håller uppe staget.
Med hjälp av måtten får jag fram en vinkel på 32,6 gr i C.
Om vi börjar med kraften i S som är 450N. Den kraften kan du dela upp i komposanter som du säger och då blir det en vertikal, nedåtgående komposant som är och en som går mot A som är lika stor. Kraften i repet mot G är också 450N så då får du en vertikal, nedåtgående kraft som är och en horisontell åt höger som är 450*1/2
Eftersom vi försummar egenvikter så är det här de enda yttre krafterna på systemet och vi summerar med horisontella positiva värden åt vänster och vertikala positiva värden nedåt
dvs de värden du också har fått. Eftersom vi definierat den horisontella komponenten positiv åt höger så får vi alltså en resulterande kraft som trycker stången mot AC.
Den vertikala kraftsumman tas upp av repet BC och aftersom inget rör sig så är den vertikala komposanten av kraften i repet lika stor som den vertikala delen i repet SG som vi just räknat ut ovan. Tan för vinkeln mellan BC och vertikalen är 2,5/1,6 vilket blir 1,5625 och vinkeln blir då 57.4° vilket ger kraften i repet
Den kraften har ju också en komposant som trycker stången mot A och den komposanten + den som vi räknade ut ovan adderas enligt (positiva värden åt vänster)
Eftersom stången är ledad kan den inte ta upp några vertikala krafter och rep kan bara ta upp dragkrafter i sin längdriktning så det här är de enda krafterna i AC resp BC.
Med reservation för räknefel så kontrollera gärna.
Nu ska vi se. Jag hakade upp mig lite på den resulterande kraften som trycker stången mot AC. Är inte helt med på vilket som trycker stången och hur. AC är väl hela stångens längd tänker jag.
Jag försöker förstå om det är någon specifik formel du använder för att ta fram resultantkrafterna.
Såg att du använde standardtrianglar i första beräkningarna.
Sedan Fv / cos för vinkeln.
Är inte heller klar i komposanten från repet BC som trycker stången mot A.
Jag gjorde lite olika pilar i bilden, vet inte om jag kanske snurrar till det ännu mer nu.
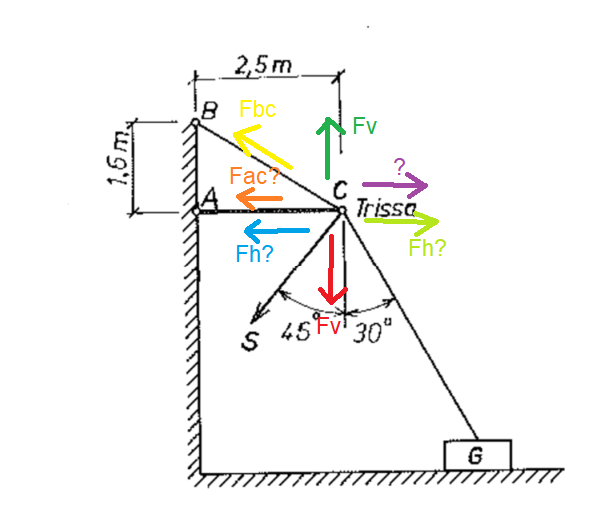
Kan bidra med en skiss från igår då jag endast beräknade FBC kraften. Det verkar tillräckligt att använda fyra krafter för att göra beräkningarna.

nejmeg skrev:Nu ska vi se. Jag hakade upp mig lite på den resulterande kraften som trycker stången mot AC. Är inte helt med på vilket som trycker stången och hur. AC är väl hela stångens längd tänker jag.
Jag försöker förstå om det är någon specifik formel du använder för att ta fram resultantkrafterna.
Såg att du använde standardtrianglar i första beräkningarna.
Sedan Fv / cos för vinkeln.
Är inte heller klar i komposanten från repet BC som trycker stången mot A.
Jag gjorde lite olika pilar i bilden, vet inte om jag kanske snurrar till det ännu mer nu.
Grunden är att en kraft kan delas upp i komposanter som ger samma påverkan som den ursprungliga kraften gör. Det gör man för att det är enklare att räkna.
Om du tittar på punkten C (trissan) så har du 4 krafter som påverkar den. Kraften FS i repet S och eftersom repet ligger över en trissa så har du samma kraft i repet mot G, FG.
Vidare har du en kraft i repet BC som jag kallar FBC och så har du en kraft i stången AC som jag kallat FAC.
Dessa fyra krafter balanserar varann eftersom punkten C inte rör sig och då vet vi att summan av krafterna är 0. Om vi då delar upp krafterna i sina vertikala och horisontella komposanter så ska summan av dessa komposanter i respektive riktning vara 0, dvs summan av alla horisontella komposanter ska vara 0 och detsamma för de vertikala.
Vi ska nu räkna ut kraften FAC och FBC och det gör vi genom att dela upp krafterna i två riktningar och väljer horisontellt och vertikalt. Vi kan välja vilka riktningar vi vill men i det här fallet är det lämpligt att välja horisontellt och vertikalt eftersom AC är horisontell och bara tar upp horisontella krafter.
Nu delar vi upp Fs i en horisontell och en vertikal komposant och gör det samma med FG. Nu kan du addera alla horisontella krafter (med tecken) och alla vertikala som jag gjort ovan och kallag Fh resp Fv
Vi har inte ändrat något från ursprungsläget utan bara slagit ihop de två krafterna i repet SG och delat upp dem i en horisontell och en vertikal del, Fh och Fv. Det gör det enklare att räkna på dem. Eftersom de är vinkelräta är kan vi räkna på var och en oberoende av varandra. Jag skrev fel i mitt förra inlägg om att vi definierat den horisontella komposanten positiv åt höger. Det ska naturligtvis vara åt vänster men slutsatsen är rätt, kraften i SG trycker stången med 93N mot A. Vertikalt har vi en kraft nedåt på 708N som skapas av kraften i repet SG.
Nu ska vi balansera Fh och Fv med kraften i stången (FAC) och kraften i repet (FBC). Eftersom stången bara kan ta upp horisontella krafter så måste den vertikala kraften Fv tas upp av kraften i repet FBC. Det innebär att den vertikala komposanten av FBC måste vara lika stor som Fv och givet vinkel mellan BC och vertikalen kan vi då räkna ut hur stor kraften i repet måste vara, FBC. Det är svaret på den ena frågan.
När vi nu vet vad FBC är och vinkeln mellan kraften och horisonten så kan vi räkna ut den horisontella komposanten av FBC som då verkar i samma riktning som stången. Den kallar jag FBCsin(a) och lägger jag ihop den med den horisontella kraften från repet SG (Fh) så får vi den kraft som ska balanseras av kraften i stången för att kraftsumman ska vara 0.
Du har lite för många pilar i din figur. Det finns bara 4 krafter som sagt. Rita in dem. Kraften i repet SG och i repet BC är lätta att rita då det säkert är dragkrafter. I stången vet du inte vilken riktning den har men du vet att den är horisontell. Den kan gå åt vänster eller höger men det spelar ingen rolll hur du ritar bara du räknar rätt så ger tecknet i ditt slutresultat rätt riktning. Om du får ett positivt svar så har du ritat rätt, blir svaret negativt så går kraften i andra riktningen.
När du ritat alla fyra krafterna så delar du upp dem i horisontella och vertikala komposanter och då ska summan i varje led vara 0 med. Du kommer att få två ekvationer med två obekanta så det går att lösa. Jag har försökt visa det ovan stegvis men är det något där jag varit otydlig så får du fråga igen.