Möjliga areor
"" L1 och L2 är rätvinkliga mot varandra. Tillsammans med x-axeln bildar de en triangel i första kvadranten. L1 går igenom origo och L2 går igenom (0,5). Linjerna skär varandra där x=2. Vilka areor kan triangeln ha?""
Så här långt har jag kommit:
L1 : y = k1 * x
L2 : Punkten (0,5) ger m = 5. y = k2 *x + 5
Sedan får jag ihop ett ekvationssystem:
k1 * k2 = -1
k1(2) = k2(2) + 5
Med PQ-formlen löste jag ekvationssystemet och fick följande lösningar:
k1 = 1/2 och 2
k2 = -2 och -1/2
För att beräkna höjden på triangeln sätter jag in x = 2. Detta ger:
Höjd 1 = 1/2(2) = 1 l.e
Höjd 2 = 2(2) = 4 l.e
Arean blir då 1/2(5*h) vilket ger svaren 2.5 a.e och 10 a.e
Enligt facit är det 20 a.e och 1.25 a.e. Vad gör jag fel?'
Tack på förhand,
MishMish skrev:Vad gör jag fel?'
Har du ritat en skiss som visar de möjliga trianglarna?
- Om ja, visa den.
- Om nej, gör det och visa den.
Yngve skrev:MishMish skrev:Vad gör jag fel?'
Har du ritat en skiss som visar de möjliga trianglarna?
- Om ja, visa den.
- Om nej, gör det och visa den.
Fall
1
Fall 2:

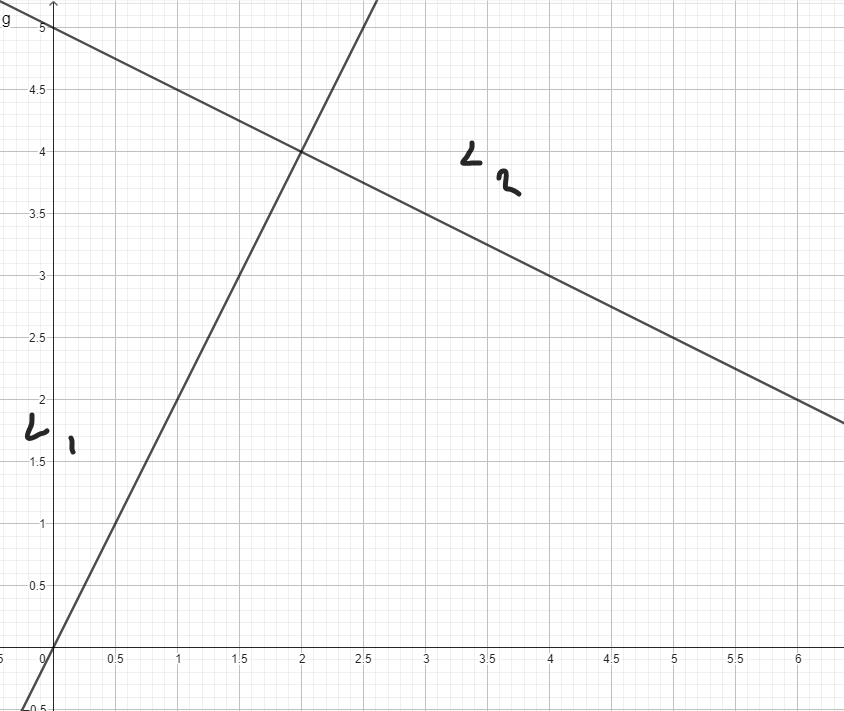
Jag förstår inte riktigt hur du räknar ut arean.
- I det ena fallet ör basens längd 2,5 l.e. och höjden 1 l.e.
- I det andra fallet är basens längd 10 l e. och höjden 4 l e.
Ahaa, nu förstår jag.
Båda trianglarna begränsas av L1, L2 och x-axeln (inte y-axeln).
Yngve skrev:Ahaa, nu förstår jag.
Båda trianglarna begränsas av L1, L2 och x-axeln (inte y-axeln).
Jahaaa, nu fattar jag. Tack!


