Modulär aritmetik

Kongruenta tal är tal som ger samma rest vid division med samma tal. Exempelvis är talen 4 och 9 kongruenta (modulo 5), då båda tal ger resten fyra vid division med talet fem. Restberäkning är klurigt, men lätt när en väl lyckas förstå (som mycket inom matten). För mig är det väldigt effektivt att tänka på moduloräkning som ett roterande kugghjul, med ett visst antal piggar. Ta exemplet med fem. Det blir ett hjul med fem piggar, där varje pigg representerar ett steg framåt på tallinjen. Ett tal kan (vid division med fem) ha resten:

Noll, då talet är delbart med fem.
Ett, då talet är ett större än ett tal delbart med fem, exempelvis 1, 6, 11, 16, osv.
Två, då talet är två större än ett tal delbart med fem, exempelvis 2, 7, 12, 17, osv.
Tre, då talet är tre större än ett tal delbart med fem, exempelvis 3, 8, 13, 18, osv.
Fyra, då talet är fyra större än ett tal delbart med fem, exempelvis 4, 9, 14, 19, osv.

Det ger oss hjulet:

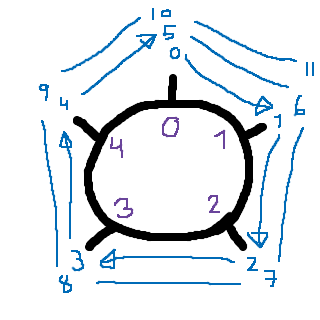
Där talet utanpå hjulet är talet, och den lila siffran inuti hjulet är resten. Dessa "hjul" ger oss även en förklaring om varför (-3) och (2) är kongruenta; minustecknet innebär helt enkelt att hjulet rullar åt motsatt håll:

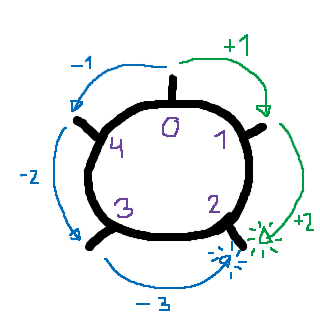
Då hamnar de på samma rest. Det gäller att alla tal med differensen fem är kongruenta med varandra, eftersom vi roterar ett visst antal platser för att komma till det mindre talets plats, och sedan hoppar vi fem platser till, för att ta oss till det större talets plats. Det är bara det att när vi hoppar fem platser framåt (eller bakåt) hamnar vi på samma plats (som har samma rest) igen. Alltså måste alla tal med differensen fem vara kongruenta (modulo 5). 

I din andra tråd frågade du om hur man gör för att hitta a i frågor som $19\equiv a (\mathrm{mod} 6)$, och det är samma taktik här. När det känns svårt att förstå, rita upp ett hjul med sex kuggar, var och en med sin rest, 0 - 5, och börja på noll. Räkna sedan uppåt, tills du kommer till nitton. Vilken rest har talet nitton? Vilka andra tal har resten nitton?