Missar lösning i cos/sin-ekvation
Hej,
Jag har följande ekvation att lösa: sin x = cos 2x
Här är min lösning, som är delvis rätt tror jag:
Problemet är att när jag kollar i facit ser jag att man hittat tre lösningar (jag har alltså bara funnit två av dem):
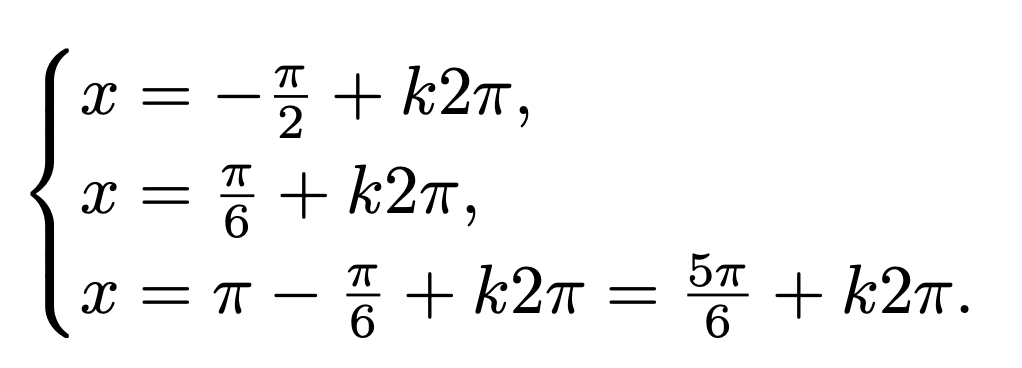
Varför missar jag den sista lösningen i mina beräkningar?
Edit: Ser också att jag får en division med 3 som inte facit har. Varför får jag det, men inte facit?
Hej.
Lösningen som leder fram till facit är antagligen via dubbla vinkeln cosinus, dvs cos(2x) = 1-2sin2(x).
Detta ger oss en andragradsekvation i sin(x), vars lösningar blir just de som står i facit.
Yngve skrev:Hej.
Lösningen som leder fram till facit är antagligen via dubbla vinkeln cosinus, dvs cos(2x) = 1-2sin2(x).
Detta ger oss en andragradsekvation i sin(x), vars lösningar blir just de som står i facit.
Tack för svaret! Du har rätt, det är den metod man använt sig av i facit.
Men, är min lösning fel? Eller fungerar den också? Tänker att det samband jag använt mig av, d.v.s. att sin x = cos (pi/2 - x) också är ett korrekt samband, eller?
Din lösning fungerar också. Du har inte missar någon lösning.
Faktum är att din lösning nr1 innehåller samtliga lösningar som facit har. Rita i enhetscirkeln så ser du.
Edit. Det är just din division med 3 av 2pik som gör att den täcker in samtliga lösningar, så inget att ändra på där.
