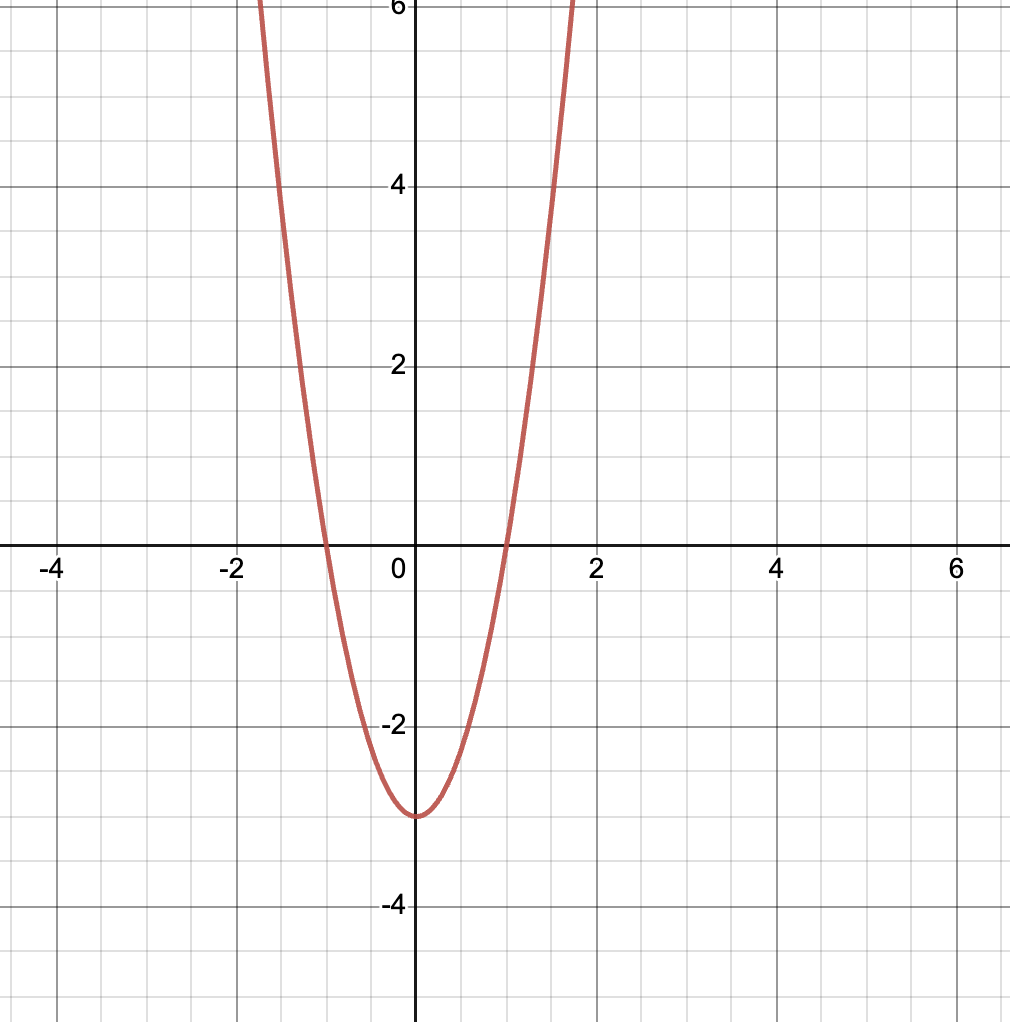
minsta värde funktionen kan anta? (Matematik/Matte 4)

Minsta värde är där integralen är så liten som möjligt.

Om du ritar upp grafen för 3t^2-3 i Geogebra så ser du att den minsta integralen som kan skapas då x>=0 är om intervallet blir där vi får med så mycket yta under x-axeln som är möjligt. Där blir ju integralen negativ.

mrpotatohead skrev:
Minsta värde är där integralen är så liten som möjligt.

Om du ritar upp grafen för 3t^2-3 i Geogebra så ser du att den minsta integralen som kan skapas då x>=0 är om intervallet blir där vi får med så mycket yta under x-axeln som är möjligt. Där blir ju integralen negativ.

Kurvan ligger väl bara över x-axeln? Hur får man fram det minsta värdet där?

Nepp.

Ja, det stämmer. Hade för stora värden på fönstret.

Men hur ska jag utnyttja denna information? (Vet inte riktigt hur jag ska fortsätta)

För som du säger så blir ju värden under x-axeln negativa.

Exakt.

Frågan är ju för vilket x-värde (ändpunkt i intervallet för integralen) som integralen blir lägst. Detta borde ju då vara där vi får så mycket yta som möjligt under x-axeln och så lite över.

Om du ska lösa den grafiskt, var tycker du det x-värdet borde vara?

mrpotatohead skrev:
Exakt.

Frågan är ju för vilket x-värde (ändpunkt i intervallet för integralen) som integralen blir lägst. Detta borde ju då vara där vi får så mycket yta som möjligt under x-axeln och så lite över.

Om du ska lösa den grafiskt, var tycker du det x-värdet borde vara?

Jaha,

x=1, den kan inte vara vid den andra ändpunkten (-3) då vi fick ett villkor att x ska vara större än 0.

Dvs en integral från 0 till 1.

Tillägg: 18 nov 2023 14:37

Sedan är det bara att lösa ut integralen så får man ut det minsta värdet det kan anta?

Det löste sig. Tack!

Hur hade man tänkt om kurvan låg över x-axeln?

Bara en tanke men du kan också lösa det algebraiskt tror jag, vilket skulle vara trevligt om funktionen blir mer komplex än en enkel andragradare:

$\displaystyle f'(x)=3x^{2}-3$

Sätt $\displaystyle f'(x)=0\implies 3x^{2}-3=0\implies x^{2}=1\implies x=\pm {1}$

Men eftersom vi redan vet att $x\ge 0$ finns det bara ett svar.

naytte skrev:
Bara en tanke men du kan också lösa det algebraiskt tror jag, vilket skulle vara trevligt om funktionen blir mer komplex än en enkel andragradare:

$\displaystyle f'(x)=3x^{2}-3$

Sätt $\displaystyle f'(x)=0\implies 3x^{2}-3=0\implies x^{2}=1\implies x=\pm {1}$

Men eftersom vi redan vet att $x\ge 0$ finns det bara ett svar.

Ja precis! Bra tanke.

Det hade nog blivit lite svårt om den låg över x-axeln?

Inte för just andragradaren men att grafa en tredjegradare och sedan dessutom avgöra i vilket intervall integralen blir minst med blotta ögat? Nej tack.

naytte skrev:
Inte för just andragradaren men att grafa en tredjegradare och sedan dessutom avgöra i vilket intervall integralen blir minst med blotta ögat? Nej tack.

Ja det hade nog inte varit det enklaste. Men algebraiskt? Ellertyp rita upp mha hjälpmedel.

Algebraiskt skulle man kunna göra på exakt motsvarande sätt om jag gjorde ovan. Kan inte tänka mig att det skulle bli supersvårt.

naytte skrev:
Algebraiskt skulle man kunna göra på exakt motsvarande sätt om jag gjorde ovan. Kan inte tänka mig att det skulle bli supersvårt.

Men blir inte det positivt svar och stort? Om man beräknar från ändpunkt till 0, då får man väl hela/halva området?

Jag förstår inte vad du menar. Om du har en uppgift på motsvarande form som den ovan men funktionen på insidan av integralen är mer komplex kan du göra exakt samma sak.

Men hur hade det största värdet räknats ut isåfall?

Genom att sätta derivatan lika med noll. OM det finns ett största värde kommer du hittade det så.

Jag kan ta ett exempel för att visa vad jag menar. Låt säga att vi har en funktion:

$\displaystyle f(x)=\int_{0}^{x}(2t^{3}-4t^{2}+2)dt$

Vi frågar oss nu om denna funktion har något maximalt värde, och i sådana fall vilket. Vi börjar med att derivera:

$\displaystyle f'(x)=2x^{3}-4x^{2}+2$

Sedan vill vi leta upp eventuella extrempunkter. Då löser vi:

$\displaystyle 2x^{3}-4x^{2}+2=0$ .

Gör så att du försöker plocka fram rötterna själv, det är bra övning! Hur som helst ser vi att de blir

$\displaystyle x_{1}=1$ , $\displaystyle x_{2,3}=\frac{1\pm \sqrt{5}}{2}$ .

Sedan undersöker du huruvida dessa punkter är globala extrempunkter eller bara lokala osv... Nu råkar det inte finnas något största värde (vilket du kan visa enkelt med ett gränsvärde) så du kan ju testa att göra det om det vill.

Och ursäkta språket men fan vad coolt att en av rötterna blev gyllene snittet! Jag bara höftade fram ett polynom.

naytte skrev:
Jag kan ta ett exempel för att visa vad jag menar. Låt säga att vi har en funktion:

$\displaystyle f(x)=\int_{0}^{x}(2t^{3}-4t^{2}+2)dt$

Vi frågar oss nu om denna funktion har något maximalt värde, och i sådana fall vilket. Vi börjar med att derivera:

$\displaystyle f'(x)=2x^{3}-4x^{2}+2$

Det är väl samma funktion som är angiven du skrivit av? Ingen derivering?

Tillägg: 18 nov 2023 16:09

Eller tänker du att det är den funktionen som är derivatan till prim funktionen och därför är det egentligen den du sätter = 0

Eller tänker du att det är den funktionen som är derivatan till prim funktionen och därför är det egentligen den du sätter = 0

Jag tror du tänker rätt här men du kan ju försäkra dig om att det blir samma sak genom att:

Skriva om integralen med analysens fundamentalsats
Derivera omskrivningen