Minimipunkt
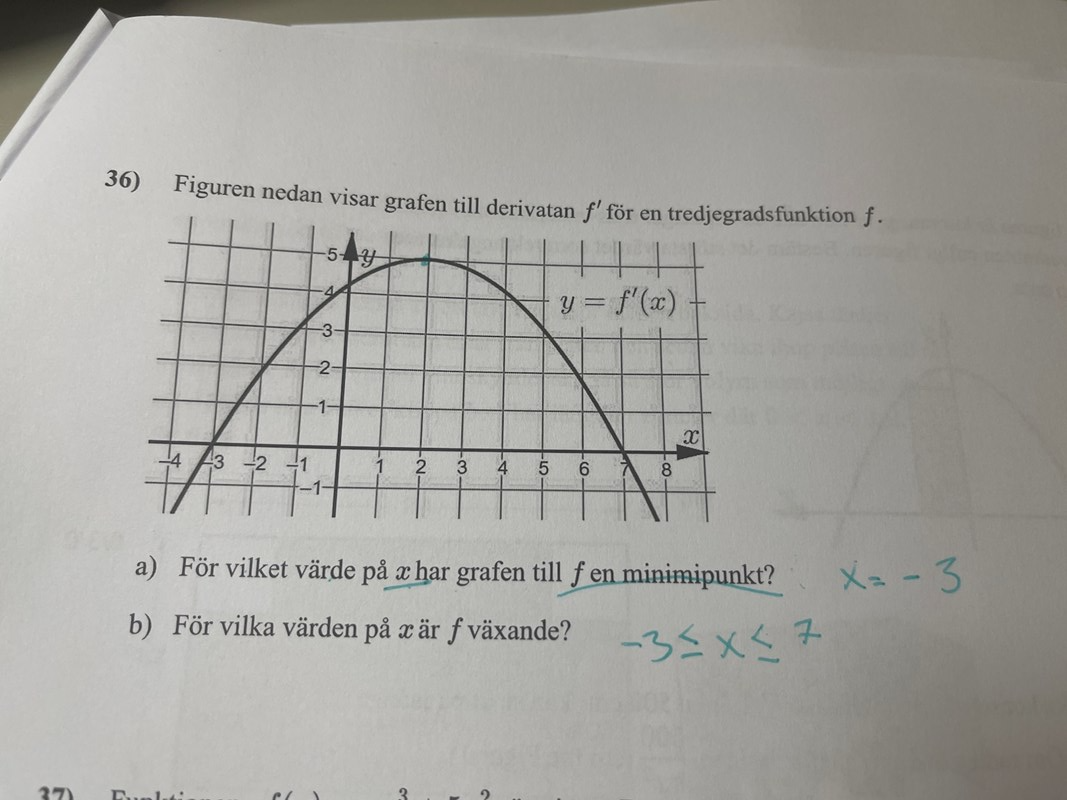hur är x=-3 en minimipunkt???? Varför just -3? Varför inte -4?
Roterad bild. /MrP, moderator
Derivatans nollställen indikerar extrempunkter för ursprungsfunktionen. Kan du se på hur derivatan byter tecken runt -3 att det är en minimipunkt?
Som MrPotatohead sa, så är derivatans nollställen en indikation av extrempunkter för ursprungsfunktionen.
För att kunna avgöra om extrempunkten då är en minimi eller maximipunkt, så måste man också ta hänsyn till andragrads derivatan av funktionen f(x), dvs f''(x) (uttalad som "f dubbel-prim av x")
Känner du till det här konceptet?
Det behöver man inte. Det räcker att kolla på teckenväxlingen runt nollstället för derivatan. Om lutningen går från negativ till positiv måste det vara en minimipunkt.
MrPotatohead skrev:Det behöver man inte. Det räcker att kolla på teckenväxlingen runt nollstället för derivatan. Om lutningen går från negativ till positiv måste det vara en minimipunkt.
Just det, right... det var ju smidigare och enklare! haha.
Men det är också därför en positiv andraderivata ger en minimipunkt. Lutningen går från negativ till positiv dvs ökar hela tiden. Och det är ju denna förändring av förändringen andraderivatan indikerar.
MrPotatohead skrev:Men det är också därför en positiv andraderivata ger en minimipunkt. Lutningen går från negativ till positiv dvs ökar hela tiden. Och det är ju denna förändring av förändringen andraderivatan indikerar.
Ja, ett sätt att lösa det är att se teckenväxlingen runt nollställen för derivatan för att kunna inse om extrempunkten blir en minimi eller maximipunkt, och ett annat sätt att lösa uppgiften är att använda sig av andraderivatan och se om det är positivt eller negativt, vilket ger om extrempunkten blir då minimi respektive maximipunkt.
