Min/max value
Hej
Jag har fastnat på den här frågan och behöver hjälp
Jag kommit fram till följande
f(x) =sinx
f'(x) =cosx
f''(x) =-sinx
Om man sätter både första derivatan och andra derivatan lika med noll så får man följande
Första derivatan
x=-pi/2+n*2pi och x=pi/2+n*2pi
Andra derivatan
X=pi+n*2pi och x=0+n*2pi
Först har jag gjort rätt?
ur detta ska man bestämma konkavitet och infektionspunkter
Jag har gjort teckentabell men har fått fel jämfört med facit
maialk skrev:Hej
Jag har fastnat på den här frågan och behöver hjälp
Jag kommit fram till följande
f(x) =sinx
f'(x) =cosx
f''(x) =-sinx
Om man sätter både första derivatan och andra derivatan lika med noll så får man följande
Första derivatan
x=-pi/2+n*2pi och x=pi/2+n*2pi
Andra derivatan
X=pi+n*2pi och x=0+n*2pi
Först har jag gjort rätt?
ur detta ska man bestämma konkavitet och infektionspunkter
Jag har gjort teckentabell men har fått fel jämfört med facit
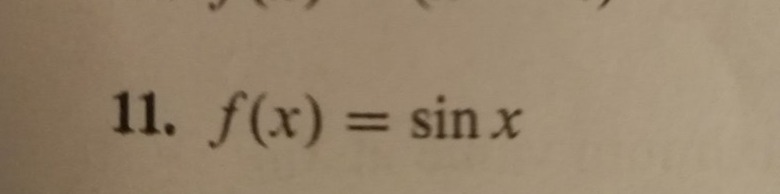
Hur lyder själva frågan?
Ladda gärna upp en bild på den.
======
Gällande din lösning:
Dina derivator är rätt och dina lösningar till f'(x) = 0 och f''(x) = 0 är rätt.
(Men lösningarna till kan skrivas på enklare sätt, nämligen x = pi/2 + n•pi respektive x = n•pi.)
Och visa gärna din teckentabell och ditt resonemang.
Yngve skrev:Hur lyder själva frågan?
Ladda gärna upp en bild på den.
======
Gällande din lösning:
Din derivara är rätt och dina lösningar till f'(x) = 0 och f''(x) = 0 är rätt.
(Men lösningarna till f''(x) = 0 kan skrivas på ett enklare sätt, nämligen x = n•pi.)
Och visa gärna dun teckentabell och ditt resonemang.

OK jag tolkar frågan som att du ska ange de intervall i vilka f(x) är konkav och vilka inflexionspunkterna är.
Yngve skrev:OK jag tolkar frågan som att du ska ange de intervall i vilka f(x) är konkav och vilka inflexionspunkterna är.
Ja, det kom jag inte till.
Jag infogade tabellen där uppe
Din teckentabell stämmer inte.
Förslag:
- Skriv ut funktionsuttrycken för både f(x), f'(x) och f''(x) till vänster i tabellen, dvs skriv t.ex. f'(x) = cos(x) till vänster.
- Utöka tabellen så att den innehåller hela intervallet från -pi till pi.
- Använd enhetscirkeln för att bestämma var det ska stå minus, noll respektive plus i tabellen.
Yngve skrev:Din teckentabell stämmer inte.
Förslag:
- Skriv ut funktionsuttrycken för både f(x), f'(x) och f''(x) till vänster i tabellen, dvs skriv t.ex. f'(x) = cos(x) till vänster.
- Utöka tabellen så att den innehåller hela intervallet från -pi till pi.
- Använd enhetscirkeln för att bestämma var det ska stå minus, noll respektive plus i tabellen.
Tack



