Min Max problem
Varför hittar man inga min och max värde för den här? 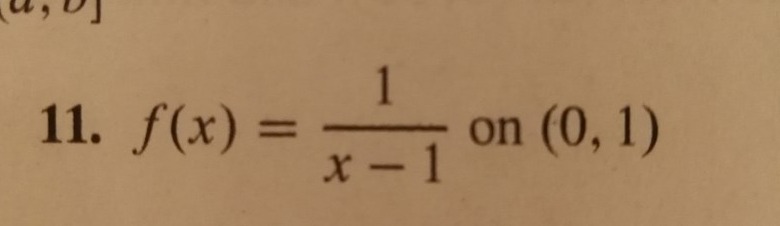
Menar du att den borde ha det?
Laguna skrev:Menar du att den borde ha det?
Ja
Tips: Intervallet (0, 1) kan även skrivas ]0, 1[ och innebär 0 < x < 1.
Ändpunkterna 0 och 1 ingår alltså inte i intervallet.
Kommer du vidare då?
Yngve skrev:Tips: Intervallet (0, 1) kan även skrivas ]0, 1[ och innebär 0 < x < 1.
Ändpunkterna 0 och 1 ingår alltså inte i intervallet.
Kommer du vidare då?
Jag har gjort så här men vet ej om det rätt
maialk skrev:Yngve skrev:Tips: Intervallet (0, 1) kan även skrivas ]0, 1[ och innebär 0 < x < 1.
Ändpunkterna 0 och 1 ingår alltså inte i intervallet.
Kommer du vidare då?
Jag har gjort så här men vet ej om det rätt
Det stämmer att derivatan saknar nollställe, vilket innebär att funktionen saknar stationära punkter.
I det aktuella intervallet så är funktionen strängt avtagande eftersom derivatan överallt där är negativ.
När x närmar sig 1 från vänster så går funktionsvärdet mot minus oändligheten. Det betyder att funktionen saknar ett minsta värde I intervallet.
När x närmar sig 0 från höger så går funktionsvärdet mot -1.
Men eftersom 0 inte ingår i intervallet så kommer x ldrig att bli lika med 0. Det innebär att funktionsvärdet aldrig når -1.
Hängde du med på det?
Yngve skrev:Det stämmer att derivatan saknar nollställe, vilket innebär att funktionen saknar stationära punkter.
I det aktuella intervallet så är funktionen strängt avtagande eftersom derivatan överallt där är negativ.
När x närmar sig 1 från vänster så går funktionsvärdet mot minus oändligheten. Der betyder att funktionen saknar ett minsta värde I intervallet.
När x närmar sig 0 från höger så går funktionsvärdet mot -1.
Men eftersom 0 inte ingår i intervallet så kommer x ldrig att bli lika med 0. Det innebär att funktionsvärdet aldrig når -1.
Hängde du med på det?
Ja, Tack så mycket




