Metrik, slutna mängder, bevis

Hej! Jag behöver hjälp med följande uppgift:

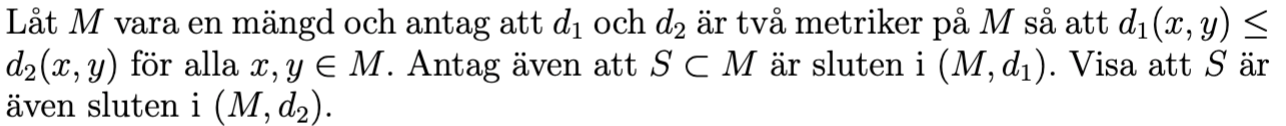
Hittills har jag:

Vill visa att S(komplement) är öppen i (M, d2) eftersom jag då visat att S är sluten i (M, d2).

Enl. def. sägs S(komplement) vara öppen om för alla x som tillhör S(komplement) så finns ett r>0: B_{x,r}<S(komplement) (B_{x,r} är bollen B_{x,r}(y)={x: d_2(x,y)<r}).

Detta betyder att jag måste visa att för varje punkt x $\in$ S(komplement) finns ett r>0 sådant att B_{x,r} är helt i S(komplement).

Hur fortsätter jag? Eller är det helt fel?

Du är på rätt väg att titta på S^c (=beteckn för komplement) . Här en idéskiss: Tag en godtycklig punkt x tillhörande S^c. Antag att varje d₂-omgivning B(x,r) innehåller en punkt utanför S^c dvs tillhörande S. För varje sådan omgivning finns en d₁ -omgivning helt belägen i B(x,r) (eftersom d₁ <= d₂) Men då tillhör x slutna höljet av S i d₁ mening och S är d₁ -slutet ==> S är lika med sitt slutna hölje ==> x tillhör S. En motsägelse till att x tillhör S^c.

Det hjälper om man inser att B₂(x, r) $\subset$ B₁(x, r) för alla x $\in$ M och r > 0.

Svara