Metod för när en del av arean ligger över och under den andra kurvan
Tänk er följande funktioner och inritade i nedanstående koordinatsystem med en nedre gräns och en övre gräns . Säg att jag vill hitta arean mellan kurvorna i detta intervall .
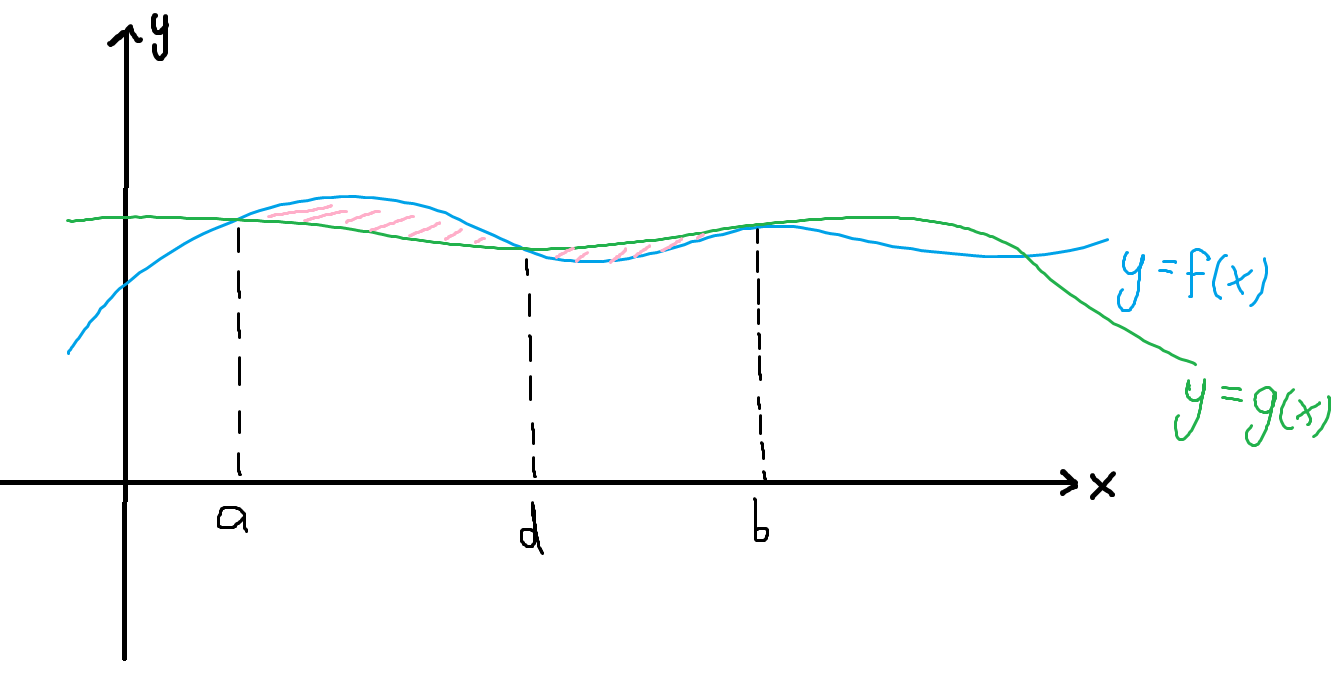
För att hitta var dessa punkter punkter ligger, där går från att vara större till mindre än , kan jag lösa olikheten då? För då borde jag få ett intervall där . Sedan vet jag ju att det då måste gälla att i .
Jag tänker att denna metod borde funka oavsett hur många "korsningspunkter" det finns. Vad tänker ni kring detta/finns det någon bättre metod? Lite mer generellt är jag ute efter en algebraisk metod för att lösa sådana här problem utan att behöva rita.
Jag skulle istället lösa ekvationen f(x) = g(x) för att hitta alla de x-värden där graferna korsar varandra. Det ger mig de relevanta intervallen.
Om du kan skissa graferna så ser du enkelt vilken funktion som är överfunktion i respektive intervall.
Om du inte kan skissa graferna så kan du ju alltid göra ett stickprov på funktionsvärden inne i intervallen för att bestämna över- respektive underfunktion.
Du kan även bestämma detta algebraiskt genom att analysera funktionsdifferensen f(x)-g(x), nollställen och derivata
Lite mer generellt är jag ute efter en algebraisk metod för att lösa sådana här problem utan att behöva rita.
Varför skulle du vilja ta fram något så dumt? Det första steget bör vara att rita!
Smaragdalena skrev:
Varför skulle du vilja ta fram något så dumt? Det första steget bör vara att rita!
Om man saknar digitala hjälpmedel och det är komplicerade funktioner så kan det vara slöseri med tid att skissa graferna.
Varför skulle du vilja ta fram något så dumt? Det första steget bör vara att rita!
Eftersom det tar tid att rita och under ett prov med flera svåra frågor och lite tid vill jag inte ödsla tid på att skissa. Missförstå mig inte - skisser är jätteanvändbara. Men när man förstår ett koncept tillräckligt bra kan man gömma det grafiska bakom algebran. Jag sitter ju liksom inte och drar in tangenter för den grafiska representationen varje gång jag använder derivatans definition.
Jag skulle istället lösa ekvationen f(x) = g(x) för att hitta alla de x-värden där graferna korsar varandra. Det ger mig de relevanta intervallen.
Men om man skulle lösa olikheten skulle man väl få "stickprovsinformationen" direkt? Alltså exempelvis om det finns många intervall skulle man ju få göra många stickprov. Men samtidigt kanske olikheter blir svårare att lösa?
Jag löser nästan aldrig olikheter, det är så lätt gjort att de blir fel - jag löser motsvarande ekvationer istället och kollar "vilken sida som är störst" för nägra väl valda värden.
Här håller jag med Smaragdalena. Jag tycker att det är svårare att lösa olikheter än ekvationer.
naytte skrev:Sedan vet jag ju att det då måste gälla att i .
Det gäller för just det exemplet du visade I trådstarten, men det behöver inte vara så generellt
Det kan mycket väl vara så att f(x) > g(x) i båda intervallen. Om du t.ex. vill beräkna arean mellan en parabel och en av dess tangenter så är parabeln övre funktion (eller undre funktion) i båda intervallen (om tangeringspunkten ingår i det område du vill areaberäkna).
Ja, men då skulle jag väl kunna se det i min olikhet jag löser? Alltså om i hela intervallet så ser man ju det när man får olikhetens lösningar.
naytte skrev:Ja, men då skulle jag väl kunna se det i min olikhet jag löser? Alltså om i hela intervallet så ser man ju det när man får olikhetens lösningar.
Pröva med ett enkelt exempel!
Tag t.ex. f(x) = x2 och g(x) = 2x-1 i intervallet [-2, 2].
Lös olikheten f(x) > g(x)
naytte skrev:Ja, men då skulle jag väl kunna se det i min olikhet jag löser? Alltså om i hela intervallet så ser man ju det när man får olikhetens lösningar.
Inte rita, och lösa olikheter i stället för ekvationer? Det skulle jag aldrig våga - jag vet hur stor risken är att nånting blir fel!
Yngve skrev:naytte skrev:Ja, men då skulle jag väl kunna se det i min olikhet jag löser? Alltså om i hela intervallet så ser man ju det när man får olikhetens lösningar.
Pröva med ett enkelt exempel!
Tag t.ex. f(x) = x2 och g(x) = 2x-1 i intervallet [-2, 2].
Lös olikheten f(x) > g(x)
Jag ritade genast upp det.
Visa spoiler
.jpg?width=800&upscale=false)
Okej, då testar jag:
Så här ser vi att kommer vara större än för varje förutom 1, då de är lika. Då kan vi dela upp integreringen i två intervall: [-2, 1] och [1, 2]:
Smaragdalena skrev:
Jag ritade genast upp det.
Poängen med exemplet handlade inte om huruvida det var enkelt/fruktsamhet att rita eller inte.
Poängen var att belysa det faktum att lösa olikheten f(x) > g(x) algebraiskt inte alltid ger ett sammanhängande intervall som jag uppfattade det att naytte tycktes tro.
Det var inte så jag menade det. Det jag menade var att om man löser f(x)>g(x) så kommer man ju få intervall för vilket olikheten gäller. Då kan man jämföra intervall(en) man får med intervallet man ska integrera över. Då vet man direkt för vilka x, f(x)>g(x) och för vilka eventuellt motsatsen gäller. Där de skär varandra borde man kunna se huruvida f(x)>g(x) eller g(x)>f(x) efteråt. Exempelvis i exemplet du gav insåg man att det fanns en skärningspunkt. Men man kunde ändå direkt säga att f(x)>g(x) efteråt eftersom intervallet man fick, för vilket f(x)>g(x) fortsatte direkt efter skärningspunkten.
OK bra, då missförstod jag dig.
naytte skrev:Där de skär varandra borde man kunna se huruvida f(x)>g(x) eller g(x)>f(x).
Där de skär varandra gäller att f(x) = g(x).
Där de skär varandra gäller att f(x) = g(x)
Yes, jag menade det som händer precis efter skärningspunkten. Ursäkta att jag uttryckte det så oklart.
Inget problem.
I det här fallet var det enkelt att lösa olikheten, men i andra fall kan det vara knepigare och då kan det vara idé att istället försöka lösa motsvarande ekvation.
Om man har löst ekvationen och står där med intervallgränser men utan kunskap om vilken funktion som är överst/underst i respektive intervall så kan man ta en genväg för att slippa lägga tid på stickprov.
- Chansa på att f(x) > g(x) i intervallet och beräkna integralen
- Om så gissade du rätt.
- Om så var det istället så att g(x) > f(x) i det intervallet och du behöver då egentligen inte beräkna eftersom du vet att den integralen har värdet .
Oj vad smart, ja det är definitivt en fin metod! Jag kommer nog börja köra på den. Tack så mycket!
naytte skrev:Oj vad smart, ja det är definitivt en fin metod! Jag kommer nog börja köra på den. Tack så mycket!
Om du ska redovisa hela lösningar så finns det en risk att din lärare tycker att just det är lite för mycket genväg och att lösningen inte håller förväntad standard.
Det kan vara smart att du redan nu frågar din lärare om ett sådant resonemang kommer att ge poängavdrag eller inte.
Räknas det ens som genväg? Det är väl bara ett logiskt resonemang? Hur som helst tackar jag igen för all hjälp!
Jag har tänkt vidare på detta och jag undrar ifall man allmänt kan säga att arean mellan två kurvor i ett intervall ges av:
Det verkar som det borde fungera, eftersom man då inte behöver ta hänsyn till vilken funktion som är överst eller underst. Det blir ju lite samma sak som den där "genvägen", men mer koncist och matematiskt uppskrivet.
Ja, det stämmer.
Det är snyggt men inte så praktiskt användbart eftersom det i allmänhet är svårt att ta fram en primitiv funktion till |f(x)-g(x)|.
Är det för att beloppet förenklas till olika funktioner beroende på vilket intervall man tittar i? Vilket betyder att man måste ta fram flera olika primitiva funktioner till varje enksilkd förenkling?
Ja. Du kommer inte ifrån att du ändå måste hitta skärningspunkterna.
Finns det ingen fiffig regel för att ta fram primitiva funktioner till absolutvärdesfunktioner? Det känns som det borde göra det... Men kanske inte?
naytte skrev:Finns det ingen fiffig regel för att ta fram primitiva funktioner till absolutvärdesfunktioner? Det känns som det borde göra det... Men kanske inte?
Inte vad jag känner till. Det handlar om att dela upp det i olika intervall och integrera varje intervall för sig, och för att kunna göra detta måste man ta fram gränderna mellan de olika intervallen.
Kan man inte utnyttja att och använda kedjeregeln baklänges?
Du har alltså att och du söker nu ett sådant att .
Vi skulle då kunna tänka att eftersom derivatan av är .
Men kedjeregeln ger då att , vilket inte stämmer.
Det blir besvärligt att hitta en sådan primitiv funktion.
Ah, okej. Så kedjeregeln kommer inte på fråga då, alltså. En intressant grej dock är att det verkar finnas en regel (yay!), men jag är för dum för att förstå den i nuläget misstänker jag.
Jag har inte tillgång till korrekt formattering på telefonen, men testa att integrera abs(x+2) på Symbolab. Den verkar nyttja en integreringsregel.
Ett annat sätt är att lösa ekvationen f(x)=g(x), och för varje beräkna , och notera vilken som var över/under - funktionen. De byter ju endast efter de skär varandra.
Notera att bara ett ett godtycklig tal du kan välja själv.
Dracaena skrev:Ett annat sätt är att lösa ekvationen f(x)=g(x), och för varje beräkna , och notera vilken som var över/under - funktionen. De byter ju endast efter de skär varandra.
Notera att bara ett ett godtycklig tal du kan välja själv.
Kommentar: Det var detta jag menade i svar #2 ...
Smaragdalena skrev:Lite mer generellt är jag ute efter en algebraisk metod för att lösa sådana här problem utan att behöva rita.
Varför skulle du vilja ta fram något så dumt? Det första steget bör vara att rita!
Det finns inga dumma tankar här på Pluggakuten, forumet är för att hjälpa eleverna samt att öka självförtroenden. Man lär sig utifrån sina spontana tankar, oavsett, tycker jag.
Uttryck dig på ett bättre sätt, SNÄLLA! /Admin
Det vore oansvarigt av mig att inte påpeka nör någon håller på att göra ett misstag. Att inte vilja rita ÄR korkat och dumt. Det är viktigt att lära sig att rita upp funktioner om man skall kunna lära sig matematik. Visst det finns tillfällen när det är svårt eller omöjligt att rita, men det är inte fallet i den här tråden.
Om någon tar illa vid sig av de ord jag använder, så ber jag verkligen om ursäkt, för det var inte min avsikt att såra någon.
Vad är det som är korkat att dumt med att vilja hitta generella, algebraiska metoder? Du ritar väl inte ut tangenter varje gång du använder derivatans definition?
Självklart kan det hjälpa förståelsen att rita, men när man väl har förståelse för vad som sker är det väl inget fel med att räkna algebraiskt?
naytte skrev:Vad är det som är korkat att dumt med att vilja hitta generella, algebraiska metoder? Du ritar väl inte ut tangenter varje gång du använder derivatans definition?
Självklart kan det hjälpa förståelsen att rita, men när man väl har förståelse för vad som sker är det väl inget fel med att räkna algebraiskt?
Hur får man förståelse utan att rita först? När man har ritat är det jättebra att räkna algebraiskt, men att rita först ökar chansen att det är rätt sak man räknar ut med ett par tusen procent.
Alltså, jag förstår ju vad det är jag räknar ut. Jag förstår att jag har två kurvor som skär varandra i olika punkter och i att det bildas områden mellan skärningspunkterna. Dessa områden ges sedan av integralerna av differensen av funktionerna i de intervallen. Vad mer ska man förstå?
Yngve skrev:Det blir besvärligt att hitta en sådan primitiv funktion.
Ett sätt att komma vidare är att använda signumfunktionen:
Nu kan man göra ett försök med partialintegration där:
Därav följer att:
Eftersom den sista integralen innehåller Diracs deltafunktion
kan den skrivas om som en summa av över alla där
Vi är alltså fortfarande tvungna att först hitta funktionens nollpunkter.
Även om detta må vara en generell lösning på integralen av absolutbeloppet av en funktion,
är det knappast en praktiskt användbar sådan.
naytte skrev:Alltså, jag förstår ju vad det är jag räknar ut. Jag förstår att jag har två kurvor som skär varandra i olika punkter och i att det bildas områden mellan skärningspunkterna. Dessa områden ges sedan av integralerna av differensen av funktionerna i de intervallen. Vad mer ska man förstå?
Till exempel för att se hur många skärningspunkter det är. För att få en "reality check" så att man ser om det värde man har räknat fram är rimligt eller inte.
Smaragdalena skrev:Det vore oansvarigt av mig att inte påpeka nör någon håller på att göra ett misstag. Att inte vilja rita ÄR korkat och dumt. Det är viktigt att lära sig att rita upp funktioner om man skall kunna lära sig matematik. Visst det finns tillfällen när det är svårt eller omöjligt att rita, men det är inte fallet i den här tråden.
Om någon tar illa vid sig av de ord jag använder, så ber jag verkligen om ursäkt, för det var inte min avsikt att såra någon.
Måste man säga "korkat och dumt" för att förklara sin åsikt?
Det är en text och inget ögons-/kroppsspråk här, hur vet man din avsikt?
Oavsett, Pluggakuten har regler och alla måste följa! /Admin






