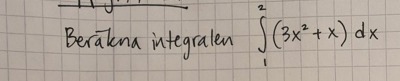mellan kurvor?
Ibland får man en kurva som skär i en annan och man begärs få fram arean mellan kurvorna enligt https://eddler.se/lektioner/areor-mellan-kurvor/
Men ibland behövs det inte och då integrerar man som vanligt. Stötte på en fråga där man skulle beräkna arean under kurvan, men då använde man formeln för "areor mellan kurvor" och satte den ena kurvan som 0. Detta medförde teckenbyte.
När är det man ska använda "areor mellan kurvor" formeln och när beräknar man en vanlig integration?
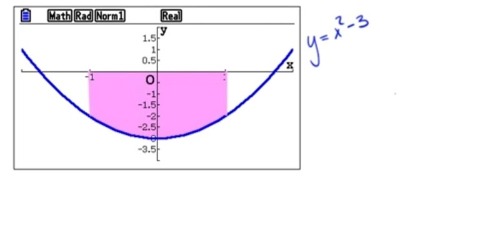 Varför kan man inte direkt göra en vanlig integral för att beräkna arean på det området? Här vill de istället man ska sätta
Varför kan man inte direkt göra en vanlig integral för att beräkna arean på det området? Här vill de istället man ska sätta
(0) -( x2-3) och beräkna integralen efter det.
Det integralen representerar är ingen area. Om du skulle beräkna integralen direkt skulle då få ett negativt tal (värdet på integralen är alltså negativt), men en area är alltid positiv.
Men visst, att beräkna integralen direkt och sedan säga att svaret måste vara positivt går också bra.
naytte skrev:Det integralen representerar är ingen area. Om du skulle beräkna integralen direkt skulle då få ett negativt tal (värdet på integralen är alltså negativt), men en area är alltid positiv.
Men visst, att beräkna integralen direkt och sedan säga att svaret måste vara positivt går också bra.
Det är alltså när den är under x-axeln då man utför denna metod? Just för att arean inte ska bli negativ?
Jag antar det. Men som sagt behöver man egentligen inte krångla till det med någon "metod". Det går lika bra att bara beräkna integralen och efteråt säga att värdet måste vara positivt.
Lite mer generallt kan man nog säga att om en funktion innesluter ett område med x-axlen i [a, b] ges arean av:
a.e.
Man tittar alltså på absolutbeloppet istället. Men viktigt att beakta är att grafen hela tiden ligger på samma sida av x-axeln i hela integreringsintervallet! Som sagt representerar integralen inte någon area.
Kan du förklara vad du menar med detta
Men viktigt att beakta är att grafen hela tiden ligger på samma sida av x-axeln i hela integreringsintervallet! Som sagt representerar integralen inte någon area.
Jag kan visa vad jag menar med ett konkret exempel. Låt säga att vi har en funktion , och att vi vill bestämma hur stor area denna funktion innesluter tillsammans med x-axeln i intervallet [-2, 2]. Den totala arean vi ska beräkna är målad i grönt.
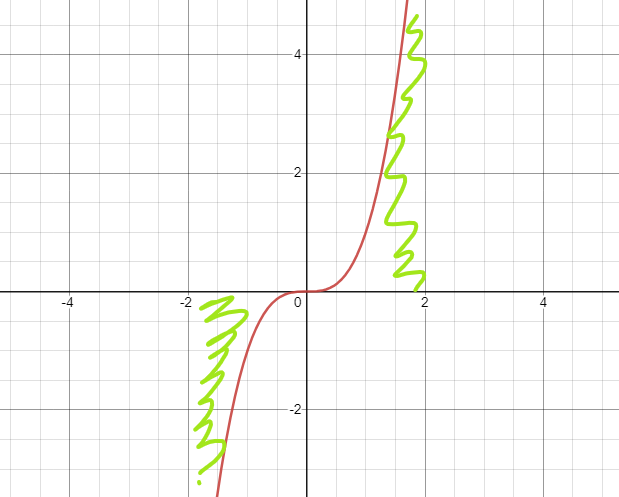
Om vi bara hade kört direkt på integralen hade vi fått värdet 0, för den "räknar" bidraget i intervallet [-2, 0] som negativt (som sagt, det är ingen area egentligen!). På grund av detta måste vi istället räkna ut detta som två integraler:
a.e.
naturnatur1 skrev:När är det man ska använda "areor mellan kurvor" formeln och när beräknar man en vanlig integration?
Du kan, om du vill, alltid använda formeln för "area mellan kurvor", dvs att arean mellan två kurvor är integralen av (den "övre" funktionen minus den "undre" funktionen).
I de fall där du endast har en funktion f(x) kan du då alltid införa en funktion g(x) = 0 (vars graf ju är lika med x-axeln).
Då blir arean mellan f(x) och x-axeln lika med
- integralen av f(x)-g(x) (dvs f(x)-0, dvs f(x)) där f(x) ligger ovanför x-axeln.
- integralen av g(x)-f(x) (dvs 0-f(x), dvs -f(x)) där f(x) ligger under x-axeln.
Du får då automatiskt rätt tecken på arean, utan att behöva hantera de fall där integralens värde blir negativt.
naytte skrev:Jag kan visa vad jag menar med ett konkret exempel. Låt säga att vi har en funktion , och att vi vill bestämma hur stor area denna funktion innesluter tillsammans med x-axeln i intervallet [-2, 2]. Den totala arean vi ska beräkna är målad i grönt.
(bild)
Om vi bara hade kört direkt på integralen hade vi fått värdet 0, för den "räknar" bidraget i intervallet [-2, 0] som negativt (som sagt, det är ingen area egentligen!). På grund av detta måste vi istället räkna ut detta som två integraler:
a.e.
Ah okej, tack!
(som sagt, det är ingen area egentligen!)
Inte? Det under grafen är väl en area? Eller menar du bara att det nödvändigtvis inte handlar om areor, utan istället även kan handla om hastighet, energi osv?
Yngve skrev:naturnatur1 skrev:När är det man ska använda "areor mellan kurvor" formeln och när beräknar man en vanlig integration?
Du kan, om du vill, alltid använda formeln för "area mellan kurvor", dvs att arean mellan två kurvor är integralen av (den "övre" funktionen minus den "undre" funktionen).
I de fall där du endast har en funktion f(x) kan du då alltid införa en funktion g(x) = 0 (vars graf ju är lika med x-axeln).
Då blir arean mellan f(x) och x-axeln lika med
- integralen av f(x)-g(x) (dvs f(x)-0, dvs f(x)) där f(x) ligger ovanför x-axeln.
- integralen av g(x)-f(x) (dvs 0-f(x), dvs -f(x)) där f(x) ligger under x-axeln.
Du får då automatiskt rätt tecken på arean, utan att behöva hantera de fall där integralens värde blir negativt.
Ah tack snälla!
Men när man beräknar med integraler, de är väl enhetslösa? Så länge de inte ska beräknas för exempelvis en area under ett visst område?
naturnatur1 skrev:
Men när man beräknar med integraler, de är väl enhetslösa? Så länge de inte ska beräknas för exempelvis en area under ett visst område?
Det beror på.
- Om koordinataxlarna är enhetslösa så blir integralens värde enhetslös.
- Om båda koordinataxlarna har enheterna längd så får integralens värde enheten area.
- Om den ena koordinataxeln har enheten tid och den andra har enheten hastighet så får integralens värde enheten längd.
- Om den ena koordinataxeln har enheten kraft och den andra har enheten tid så får integralens värde enheten energi.
Och så vidare.
Generellt sett gäller att integralens värde får den enhet som är produkten av de ingående koordinataxlarnas enheter.
Kan du komma på varför det är så?
Och om det är en beräkning av en integral utan koordinataxlar så kan man alltså inte utgå från någon enhet?
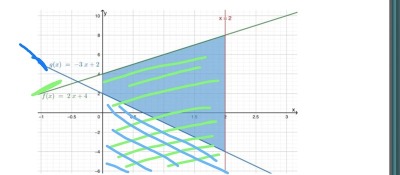
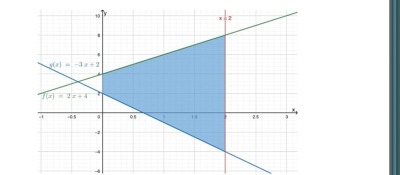 Jag verkar inte förstå riktigt hur den blåa sträckan fås genom att endast ta f(x)- g(x).
Jag verkar inte förstå riktigt hur den blåa sträckan fås genom att endast ta f(x)- g(x).
Vart går f(x) ner, är inte det bara till x-axeln eller är det hela vägen ner?
Kan du komma på varför det är så?
Det är väl för att man får tal på x och y axeln och sedan när man multiplicerar ihop dessa fås det som arean av området och beroende på vad det är som anges i x respektive y är vad arean kommer motsvara (energi, hastighet m.m)
Men jag förstår inte varför man behöver integrera först? (Eller om du var ute efter det svaret jag angav)
naturnatur1 skrev:Och om det är en beräkning av en integral utan koordinataxlar så kan man alltså inte utgå från någon enhet?
Hur menar du "utan koordinataxlar"?
Jag verkar inte förstå riktigt hur den blåa sträckan fås genom att endast ta f(x)- g(x).
Det blåa är ett område i koordinatsystemet, inte en sträcka.
Vart går f(x) ner, är inte det bara till x-axeln eller är det hela vägen ner?
Jag antar att du ska beräkna arean av det blåa området.
Då kan du använda metoden att integrera ("övre" funktionen minus "undre" funktionen).
Du behöver då inte ta hänsyn till x-axeln alls.
Yngve skrev:naturnatur1 skrev:Och om det är en beräkning av en integral utan koordinataxlar så kan man alltså inte utgå från någon enhet?
Hur menar du "utan koordinataxlar"?
Jag tänker om man bara får en integral som ska beräknas, exempelvis såhär:
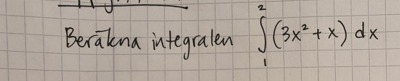
Jag verkar inte förstå riktigt hur den blåa sträckan fås genom att endast ta f(x)- g(x).
Det blåa är ett område i koordinatsystemet, inte en sträcka.
Jo det stämmer. Jag uttryckte mig fel.
Vart går f(x) ner, är inte det bara till x-axeln eller är det hela vägen ner?
Jag antar att du ska beräkna arean av det blåa området.
Då kan du använda metoden att integrera ("övre" funktionen minus "undre" funktionen).
Du behöver då inte ta hänsyn till x-axeln alls.
f(x) går alltså hela vägen ner och inte bara till x-axeln? genom att subtrahera g(x) får vi bort området under dens linje, som även f(x) rörde (just för att den fortsätter hela vägen ner)? Hoppas det inte blev rörigt och att du hänger med på vad jag menar
naturnatur1 skrev:
Jag tänker om man bara får en integral som ska beräknas, exempelvis såhär:
Ja, då kommer integralens värde att sakna enhet
f(x) går alltså hela vägen ner och inte bara till x-axeln? genom att subtrahera g(x) får vi bort området under dens linje, som även f(x) rörde (just för att den fortsätter hela vägen ner)? Hoppas det inte blev rörigt och att du hänger med på vad jag menar
Jag försöker förklara det så här:
f(x) och g(x) beskriver respektive grafs höjd ovanför x-axeln.
Eftersom f(x) > g(x) överallt i det aktuella området så kommer differensen f(x)-g(x) att vara avståndet mellan de två graferna, se bild.

Det är detta avstånd som sedan integreras från den undre gränsen till den övre gränsen och integralens värde ger då arean av det blåa området.
Nu vet jag inte om jag uppfattar det rätt, men hur kan det bara vara ovanför x-axeln? Arean täcker också en liten del nedanför x-axeln.
Kan man måla upp det så?
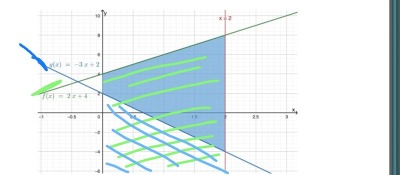
Den gröna är hela från f(x) och ned, medan den blåa täcker det nedanför g(x). Subtraheras dessa från varandra (med övre resp under integrationsgräns 0 och 2) så kommer vi få ut den blåa arean?
naturnatur1 skrev:Nu vet jag inte om jag uppfattar det rätt, men hur kan det bara vara ovanför x-axeln? Arean täcker också en liten del nedanför x-axeln.
Är du med på att
- f(x) beskriver positionen relativt x-axeln för grafen till y = f(x)? Dvs om f(x) > 0 så är positionen positiv och grafen ligger då ovanför x-axeln. Om f(x) < 0 så är positionen negativ och grafen ligger då under x-axeln.
- g(x) beskriver positionen relativt x-axeln för grafen till y = g(x)? Dvs om g(x) > 0 så är positionen positiv och grafen ligger då ovanför x-axeln. Om g(x) < 0 så är positionen negativ och grafen ligger då under x-axeln.
Kan man måla upp det så?
Den gröna är hela från f(x) och ned, medan den blåa täcker det nedanför g(x). Subtraheras dessa från varandra (med övre resp under integrationsgräns 0 och 2) så kommer vi få ut den blåa arean?
Nej, så kan man inte se det. Det skulle i så fall innebära att integralen av f(x) från 0 till 2 skulle vara lika med plus (eller minus) oändligheten.
Titta istället på bilden i svar #16. Där beskriver jag vad f(x)-g(x) innebär.
Är du med på att
- f(x) beskriver positionen relativt x-axeln för grafen till y = f(x)? Dvs om f(x) > 0 så är positionen positiv och grafen ligger då ovanför x-axeln. Om f(x) < 0 så är positionen negativ och grafen ligger då under x-axeln.
- g(x) beskriver positionen relativt x-axeln för grafen till y = g(x)? Dvs om g(x) > 0 så är positionen positiv och grafen ligger då ovanför x-axeln. Om g(x) < 0 så är positionen negativ och grafen ligger då under x-axeln.
Ja
Nej, så kan kan inte se det. Det skulle i så fall innebära att integralen av f(x) från 0 till 2 skulle vara lika med plus (eller minus) oändligheten.
Logiskt. Nu när du säger det.
Titta istället på bilden i svar #16. Där beskriver jag vad f(x)-g(x) innebär.
Har kollat och försökt klura. Men jag förstår inte varför punkterna placeras där och inte vid slutet av det blåa området åt höger sida. Tror jag också rör till det eftersom det blåa området sträcker sig både ovanför x-axeln och nedanför x-axeln.
Jag vet inte om man kan tänka så men.. bara för att underlätta.. säg att f(x) är 5 och g(x) är 3, det emellan är alltså 2 (Nu använde jag dock längder och inte area)
Men jag verkar fortfarande inte helt förstå hur differensen av dessa ger upphov till det blåa området. Det kanske är något jätte uppenbart men det har inte klickat än för mig.
naturnatur1 skrev:
Har kollat och försökt klura. Men jag förstår inte varför punkterna placeras där och inte vid slutet av det blåa området åt höger sida. Tror jag också rör till det eftersom det blåa området sträcker sig både ovanför x-axeln och nedanför x-axeln.
Jag vet inte om man kan tänka så men.. bara för att underlätta.. säg att f(x) är 5 och g(x) är 3, det emellan är alltså 2 (Nu använde jag dock längder och inte area)
Men jag verkar fortfarande inte helt förstå hur differensen av dessa ger upphov till det blåa området. Det kanske är något jätte uppenbart men det har inte klickat än för mig.
OK, jag tror att det är väl investerad tid för dig att läsa teoriavsnittet i din mattebok eller på annat stölle om definitionen av integraler.
Och att sedan koppla det till hur det blåa området kan ses som att vara uppbyggt av oändligt många oändligt tunna "strimlor".
Om du inte får ut något av din mattebok kan du läsa motsvarande här eller söka på "integraler" på Youtube.
Vi ska nog få polletten att trilla ner ska du se. Då kommer allt att kännas betydligt enklare.
Kolla in källorna och ställ sedan en massa frågor här om allt du vill att vi förklarar närmare.
Har läst i matteboken och förstår att det är uppbyggt av många små strimlor. Hade inga problem med det i matte 3 men nu när det kommer i matte 4 och jag kollade på detta exemplet tyckte jag att jag inte var helt med på banan. Ska kolla vidare på fler källor och tänka vidare och återkomma om jag inte kommer någonstans. Tack snälla!
Tillägg: 2 nov 2023 23:12
Tack för hjälpen!!
naturnatur1 skrev:
Tillägg: 2 nov 2023 23:12
Tack för hjälpen!!
Betyder det att polletten har trillat ner?
Yngve skrev:naturnatur1 skrev:
Tillägg: 2 nov 2023 23:12
Tack för hjälpen!!
Betyder det att polletten har trillat ner?
För denna fråga tror jag att jag har förstått nu, men det här med att avgöra gränserna och övre respektive undre funktion känner jag att jag måste öva mer på
OK bra, det är definitivt ett steg framåt!
Yngve skrev:OK bra, det är definitivt ett steg framåt!
Tackade innan men tack igen, det betyder enormt. Lär mig mycket av dig!