Mekanik tröghetsmoment
Hej!
Flera gånger när jag ska räkna ut tröghetsmomentet så kommer detta upp i lösningsförslaget när jag inte får rätt på det.
.
Det är när jag räknar på tunna lätta stänger. Jag hittar ej detta i formelsamlingen, är det något jag bara ska förstå av mig själv eller något jag kan få fram genom att titta på något annat tröghetsmoment och räkna lite?
Här är formelsamlingen om det behövs:


Om en stav är lätt betyder det att den inte har någon massa och alltså inte bidrar till tröghetsmomentet.
Okej, tack för svar! Men vad är det då som jag har markerat med gult i lösningsförslaget på bifogad uppgift? är klotet.
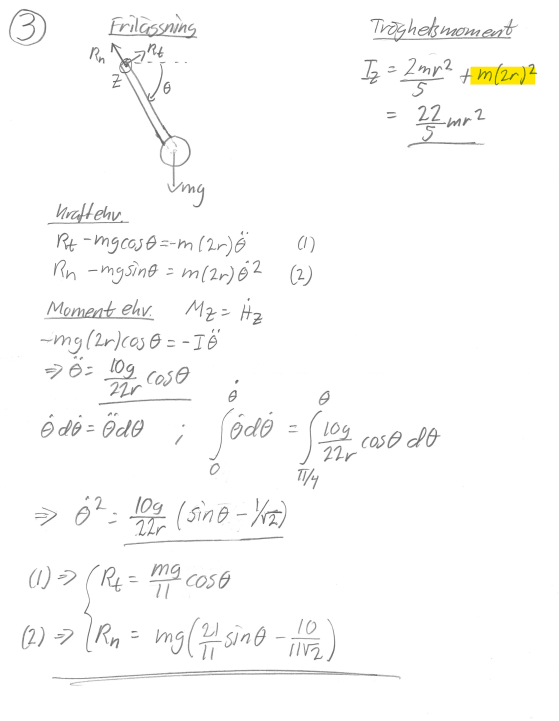
Det är Steiners sats. Tröghetsmomentet kring axeln genom O är lika med tröghetsmomentet kring en parallell axel genom masscentrum plus tröghetsmomentet kring axeln genom O för en partikel med massan m placerad i masscentrum.
Tillägg: 4 aug 2024 14:33
Aha, det flög mig över huvudet! Tack för hjälpen!
Samma kommer även på denna a- uppgiften. 
 I formelsamlingen är det närmaste jag hittar tröghetsmomentet för en hel cirkelring den för en cirkelskiva, och tycker då att är definitionen.
I formelsamlingen är det närmaste jag hittar tröghetsmomentet för en hel cirkelring den för en cirkelskiva, och tycker då att är definitionen.
Aorta skrev:Samma kommer även på denna a- uppgiften.
I formelsamlingen är det närmaste jag hittar tröghetsmomentet för en hel cirkelring den för en cirkelskiva
Du behöver inte formelsamlingen för tröghetsmomentet av (en del av) en cirkelring kring cirkelns mittpunkt.
Använd bara definitionen av vad tröghetsmoment är. (Alla dessa andra formler är inte definitioner. Det är sådant som man också kan räkna ut. Det är bara för att underlätta lite att de står tabellerade i formelsamlingar.)
Det är ju annars ganska enkelt att integrera fram resultatet i detta fall.
Ix = .
Tack för hjälpen! Ännu en undring kring Steiners sats: På dessa två exemplen ser jag ej varför de skrivit och inte .Här handlar det dock om symmetri och spegelplan, det kanske är någon speciell tanke då.
På dessa två exemplen ser jag ej varför de skrivit och inte .Här handlar det dock om symmetri och spegelplan, det kanske är någon speciell tanke då.
Obs de beräknar tröghetsprodukter här, inte tröghetsmoment. Därav skillnaden.
Tack för förtydligandet!




