Mekanik: rörelsemängden bevaras vid sammanstötning
Hej!
Jag kikar på följande uppgift och lösningsförslag
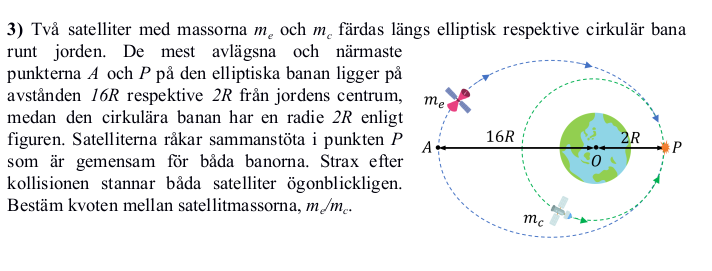

Det gulmarkerade försöker jag förstå.
Eller specifikt, meningen att rörelsemängden bevaras. Jag kom fram till alla hastigheter och så i min lösning men sen fastnade jag. Detta verkar vara nyckelinsikten.
VI vet att
Om de har samma och motriktade hastigheter i punkten P skulle vi ju ha
Men de har ju inte samma initialhastigheter. Eller vad har jag missat? Är det för att man betraktar båda som ett system och säger att inga yttre krafter påverkar?
Hur kan man se att rörelsemängden bevaras när de kommer till vila efter stöten?
Ja och nej. Det finns ju yttre krafter (gravitationen), men en krock sker under en mycket kort tid och gravitationskraften är försumbar jämfört med krockkrafterna. Så man kan försumma den impuls som gravitationen bidrar med under den korta tid som krocken varar. Så det blir i praktiken som om inga yttre krafter fanns, för den beräkning som vi gör här. Men efter krocken så blir gravitationen relevant igen.
PATENTERAMERA skrev:Ja och nej. Det finns ju yttre krafter (gravitationen), men en krock sker under en mycket kort tid och gravitationskraften är försumbar jämfört med krockkrafterna. Så man kan försumma den impuls som gravitationen bidrar med under den korta tid som krocken varar. Så det blir i praktiken som om inga yttre krafter fanns, för den beräkning som vi gör här. Men efter krocken så blir gravitationen relevant igen.
Got you! Behöve damma av lite gammal kunskap, mekanikboken jag har visade sig ha rubriken Rörelsemängden för hela systemet bevaras vid stöt under kapitlet för stötar.
Tack för dininput!


