Mekanik - Provfråga 6. Lutande metallstav med änden i en vattenmassa

Jag har en fråga om Arkimedes princip. Varav jag delvis kuggade på en fråga om det. Jag utgick från det jag trodde stämde men min lärare tänkte på ett sätt som jag känner är främmande. Jag frågade honom om detta men jag känner mig fortfarande osäker till exakt hur mitt tankesätt var inte korrekt för denna fråga.

Det var ett tag sen som jag gjorde frågan, men jag kommer ihåg kontentan av uppgiften hyggligt. Problemet är att jag inte har kvar själva formuleringen av frågan utan endast min lösning och hans lösning. Utifrån det har jag själv gjort en kort beskrivning av vad uppgiften går ut på nedanför tillsammans med en bild. Därefter visar jag kortfattat min lösning och senare den rätta lösningen. Men jag kommer betona den del som jag fick fel på och vad man skulle ha gjort.

En homogen metallstav är fäst till en punkt P och lutar ned med vinkeln $Ψ$ på trettio grader. En fjärdedel av staven längst ut befinner sig under ytan av en vattenmassa vilket är orsaken till att staven är stillastående. Bestäm densiteten av staven ifall vattnets densitet är $1000 [\frac{k g}{m^{3}}]$ .

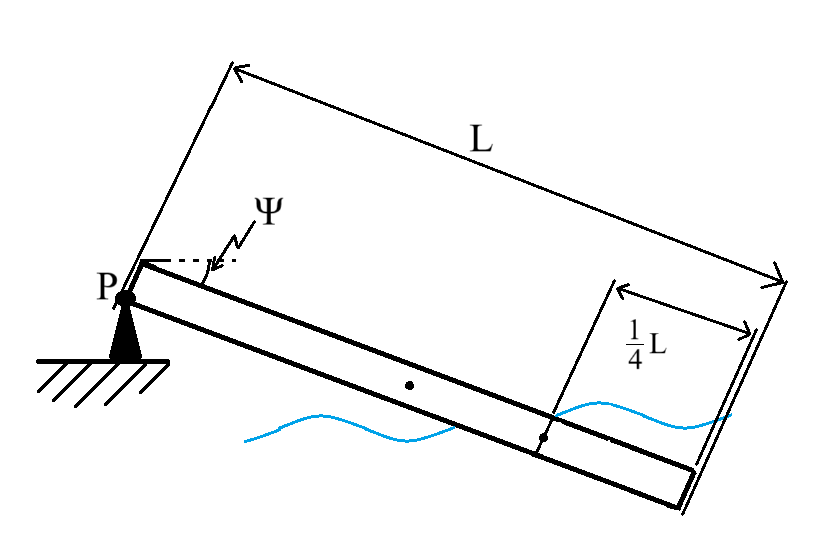
Två prickar fanns i mitten och tre fjärdedelar nedför staven för att ge en bättre bild på längderna. Allt roterar kring punkten P.

Rakt av kan man göra slutsatsen att mittersta punkten är tyngden, eftersom att staven är homogen. Därefter finns det en lyftkraft i den nedsjunkna fjärdedelen av staven. Summan av dem här två krafterna är lika med noll. Och dessutom har båda krafterna varsin volym där den ena lyfts av vattnets densitet och den andra dras ned av stavens densitet, dvs tyngd.
Staven betecknas med s, vattnet med v. De båda har två olika avstånd till punkten P.

$F_{S} r_{S} = F_{V} r_{V} ρ_{S} V_{S} g \cdot r_{S} = ρ_{V} V_{V} g \cdot r_{V}$

Eftersom att en fjärdedel av staven är under vattnet så blir $V_{V} = V_{S} \frac{1}{4}$

$ρ_{S} V_{S} g \cdot r_{S} = ρ_{V} V_{S} \frac{1}{4} g \cdot r_{V} ρ_{S} V_{S} g \cdot r_{S} = ρ_{V} V_{S} \frac{1}{4} g \cdot r_{V} ρ_{S} r_{S} = \frac{1}{4} ρ_{V} r_{V} ρ_{S} = ρ_{V} \frac{1 r_{V}}{4 r_{S}}$

Här fortsätter resonemanget över till längderna mellan krafterna och punkten P. Den första längden som är enklast att avläsa är tyngden för metallstaven.

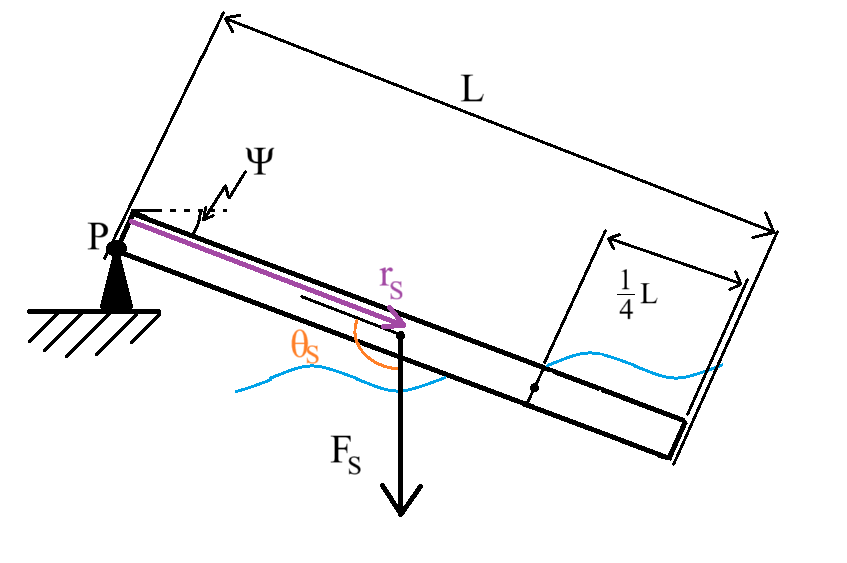
Vinkeln till tyngdkraften kan uttryckas på följande vis, $θ_{S} = Ψ + 90 °$ , och avståndet till, $\frac{1}{2} L$ . Detta ger oss följande uttryck; $r_{S} = \frac{1}{2} L \cdot \sin (Ψ + 90 °)$

Därefter har vi längden till lyftkraften, $r_{V}$ . Här gjorde jag fel. Jag visar min lösning först och därefter den korrekta lösningen, därefter ger jag slutresultatet till bägge ekvationer.

För båda resonemang blir vinkeln samma oavsett hur lång avståndet blir. Detta är formeln för dess vinkel, $θ_{V} = 90 ° - Ψ$ .

Jag resonerade att lyftkraften var positionerad i mitten av volymen till den nedsjunkna fjärdedelen. Därmed måste längden bli tre fjärdedelar plus en åttondel, eftersom att kraften måste vara i mitten av den nedsjunkna volymen, se bild nedan.

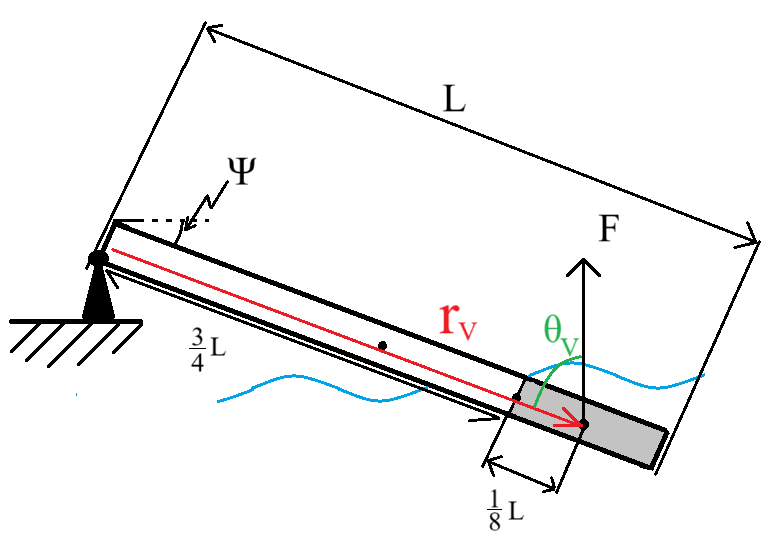
Med detta resonemang skulle avståndet bli lika med $\frac{7}{8} L$ . Men detta visar sig inte vara korrekt. Min lärare antog att avståndet istället blev $\frac{3}{4} L$ . Jag vill inte dela med mig våran diskussion i sin helhet men jag frågade följande; Innebär det att längden blir 3/4 oavsett vart flytkraften befinner sig på den nedsjunkna delen av brädan?, han svarade ja.

Detta blev ekvationerna utifrån allt som var angett, min ekvation, därefter hans.

$ρ_{S} = \frac{7 \sin (90 ° - Ψ)}{16 \sin (90 ° + Ψ)} ρ_{V}$

Mitt svar, jag valde att behålla Psi som variabel, detta gav ett svar på 437,5 $[\frac{k g}{m^{3}}]$

$ρ_{S} = \frac{3}{8} ρ_{V}$

Hans svar, 375 $[\frac{k g}{m^{3}}]$ .

Jag kan ge en bild på hur han löste uppgiften.

Men jag känner att detta inte hjälper att förklara varför lyftkraftens avstånd är bestämt tre fjärdedelar trots att den nedsjunkna volymen kan i teorin vara tre mil lång medans resten av staven är bara någon meter i längd. Det känns för osammanhängande för mig. Jag är väldigt tacksam för någon förklaring gällande hur man ska tänka med vridmoment och lyftkrafter, specifikt i denna uppgift.

Lyftkraften angriper vid tyngdpunkten för den tänkta undanträngda volymen. Alltså, du har rätt och avståndet ska vara 7/8L.

Det syns till och med i din lärares kladdiga figur:

Där denne kallar avståndet $r_L$ som löper fram till mitten av delen under vatten i figuren.

Därefter när momentet från lyftkraften ska ställas upp byts variabeln helt plötsligt ut:

Här heter den istället $r_2 = \dfrac{3L}{4}$ . Oavsett vad som hänt är detta ett uppenbart fel, baserat på enkel fysik.

Ditt tankeexperiment med en teoretiskt flera kilometer lång stav är ett väldigt bra motargument och om din lärare inte lyssnar på det är denne nog för stolt. Jag rekommenderar att du kräver en bedömning av en annan lärare.

Edit:

Förövrigt är 437.5 kg/m3 rätt svar. Då detta är ett ganska enkelt experiment att utföra hade det varit så otroligt roligt om du motbevisade läraren genom att utföra det och presentera resultaten.

Tack! Jag kände att jag behövde veta hur andra tolkade denna uppgift. Fastän jag utgår enbart från minne gällande formuleringen av uppgiften känns det lite konstigt med hans resonemang. Jag såg dessutom att det finns en x/2 längst ut av r_L, och jag antar att det kanske var just den L/8 som han kanske glömde bort. Provet var dock ett tag sen så detta är mer för nyfikenhets skull, och idéen med en laboration skulle faktiskt vara roligt att utföra som motbevis. Tack så mycket för rådet och svaret!

Svara