Mekanik pendel
Hej! Jag skulle behöva hjälp att förstå ett steg i deriveringen i denna uppgift. Det är det jag har markerat med gult. Min tanke om hur de kommer fram till det finns på bild nedan, är det korrekt? Jag förstår ej integrationsgränserna på någon av integralerna. Integrationsgränserna på andra integralen är . är given startgrad, men ? Den första integralen är jag en med på varken övre eller undre gränsen.

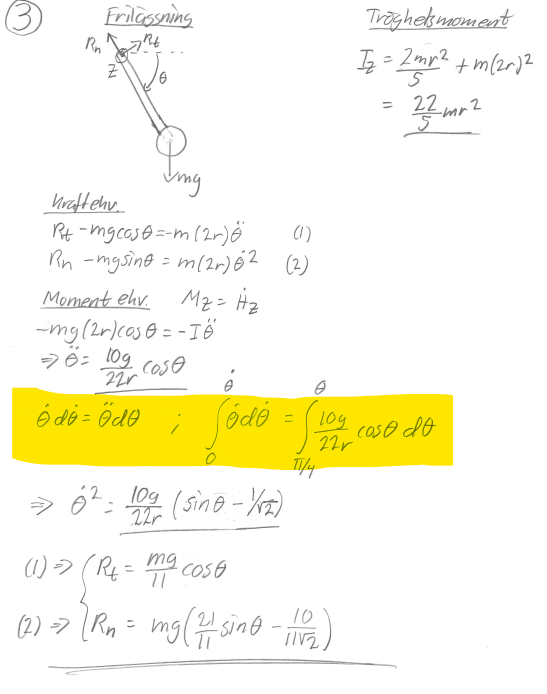

För att beräkna de efterfrågade krafterna behöver vi och .
Från momentekvationen har vi redan ett uttryck för . Det som saknas är alltså ett uttryck för
För att beräkna använder lösningsförslaget en trickbetonad lösning som går ut på att integrera över ett vinkelintervall . Om man inte är bekväm med billiga trick kan man istället bestämma genom en enkel energibetraktelse (energin bevaras, vilket ger vinkelhastigheten för alla vinklar).
I lösningen integrerar man från startögonblicket till en godtycklig slutvinkel , därför går den integralen mellan dessa två värden.
I startögonblicket är vinkelhastigheten 0, dvs Därför börjar integralen som integrerar över vinkelhastigheten på 0. Sedan slutar den vid den godtyckliga hastigheten som är vinkelhastigheten vid den godtyckliga slutvinkeln . Det är just detta vi behöver sätta in i kraftekvationen. Är du med?
Jag skulle också rekommendera dig att beräkna genom energins bevarande bara för att se att man inte måste använda opedagogiska matematiska spetsfundigheter utan faktiskt kan använda riktig fysik.
Lösningsförslaget har förövrigt missat en faktor 2 vid integreringen och får därför inte ett helt korrekt svar.
Tack för förklaringen! Jag har följt ditt råd och använder mig av energibetraktelsen. Jag får dock inte riktigt till det. Jag får inte rätt på . Jag har i energiekvationen tänkt att energin bevaras och att i läge noll är den kinetiska energin noll och den potentiella . I läge ett är den kinetiska energin (jag har missat en kvadrerad tvåa i min uträkning här) och får då . Efter att ha sett vad det ska bli misstänker jag att jag har missat något med trögheten som jag borde ha med i beräkningarna.

T = (1/2)Iz. Känd formel. Står säkert i boken - någonstans.
Tänk sedan på att den potentiella energin borde minska då ökar. Så omvänt tecken på V är ett förslag.
Tack för hjälpen! Nu har jag löst men för får jag fortfarande ej ut rätt svar. När jag kollar närmare på lösningsförslaget är högerledet i ekv.1 negativt och högerledet i ekv.2 positivt. Detta hade jag ej tidigare tänkt på, men förstår att jag har räknat med fel (helt motsatt) riktning på accelerationerna i både ekv. 1 och 2. Jag får nu fel tecken på parentesen i mitt uttryck för men blir rätt.

Du behöver minustecken på V0 också.

Hur kommer det sig? Är nollnivån vald till O då?
Ja, det är väl det enklaste att tänka sig. Du befinner dig då under nollnivån så potentialen bör vara negativ.
Tack för all hjälp!


