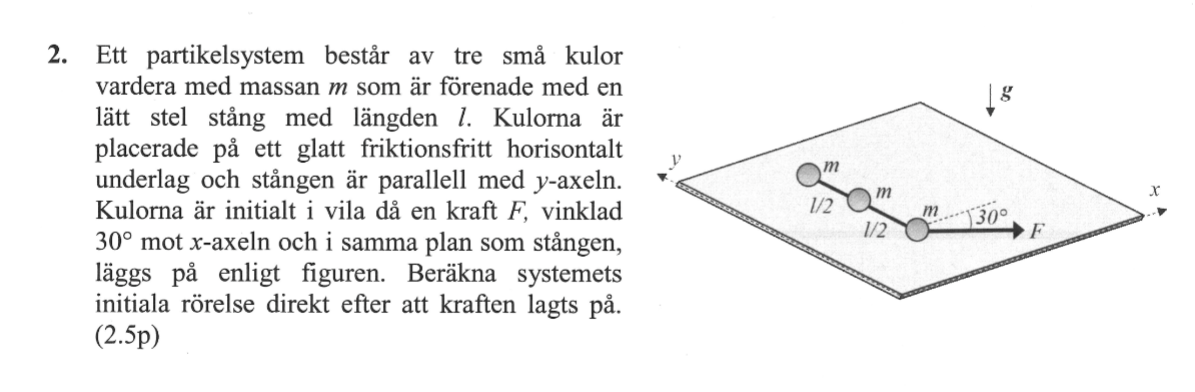
Mekanik partikelsystem

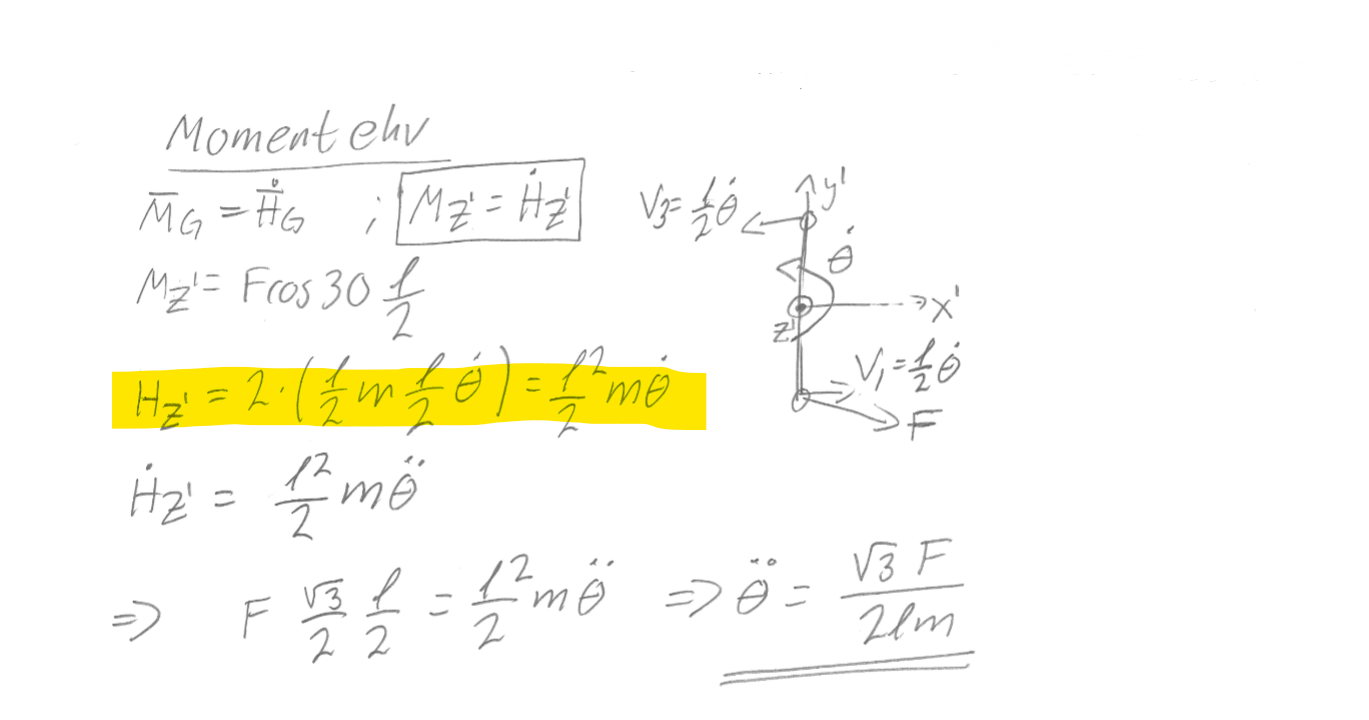
Du behöver på något sätt beräkna rörelsemängdsmomentet $H=I_o\dot{\theta}$ kring tyngdpunkten.

Eftersom massorna är små kan du se dem som punktpartiklar.

En punktpartikel på avståndet $L/2$ från rotationscentrum bidrar med tröghetsmomentet $m(L/2)^2$. Partikeln i masscentrum bidrar inte. Vi får alltså

$I_0=m(L/2)^2+m(L/2)^2=\frac{mL^2}{2}$

$H=I_0\dot{\theta}=\frac{mL^2}{2} \dot{\theta}$

Du kan också se det som att vardera punktmassa (förutom den i centrum) bidrar med $H_p=r\cdot mv$ till $H_{tot}$, där hastigheten är $v=\frac{L}{2}\dot{\theta}$. Du får då naturligtvis samma uttryck

$H_{tot}=\frac{L}{2}m\cdot \frac{L}{2}\dot{\theta}+\frac{L}{2}m\cdot \frac{L}{2}\dot{\theta}=\frac{mL^2}{2}\dot{\theta}$

Ursäkta sent svar! Tack för hjälpen!