Mekanik: omloppstidssamband
Hej!
Jag har haft lite problem med sådana här uppgifter på sistone. De handlar om omloppstider.
Jag försöker förstå lösningsförslaget till denna uppgift:


För det första har jag lite svårt att förstå rent intuitivt hur vi kan få fram relationen mellan en observerad omloppstid och den verkliga omloppstiden. Hur kan man rent intuitivt förstå hur de skiljer sig åt?
Sen har jag lite svårt att förstå vad lösningsförslaget gör, steg 1) hänger jag med på men inte riktigt steg 2). Jag förstår inte vad relationen mellan och är, alltså vad som avses med . Är det punkten som amatörastronomen "ser" som ?
Resten känns ok; Jag tolkar det som att man med menar längden av cirkelsektorn mellan och , då vid cirkelrörelse.
Det algebraiska fifflet som man ägnar sig åt i slutet hänger jag med på, om jag bara förstår vad innebörden av är!
coffeshot skrev:För det första har jag lite svårt att förstå rent intuitivt hur vi kan få fram relationen mellan en observerad omloppstid och den verkliga omloppstiden. Hur kan man rent intuitivt förstå hur de skiljer sig åt?
Det finns geostationära satelliter, till exempel för TV.
Du har säkert sett parabolantennerna även om du inte har en själv.
Pieter Kuiper skrev:coffeshot skrev:För det första har jag lite svårt att förstå rent intuitivt hur vi kan få fram relationen mellan en observerad omloppstid och den verkliga omloppstiden. Hur kan man rent intuitivt förstå hur de skiljer sig åt?
Det finns geostationära satelliter, till exempel för TV.
Du har säkert sett parabolantennerna även om du inte har en själv.
Yes, geostationära satelliter har jag lite koll på från föreläsning om centralrörelse i rymden. De vill följa jordens rörelse och befinner sig runt ekvatorn. Men jag förstår fortfarande inte vad lösningsförslaget avser med och , och varför den observerade omloppstiden skiljer sig från den verkliga.
coffeshot skrev:Pieter Kuiper skrev:Det finns geostationära satelliter, till exempel för TV.
Du har säkert sett parabolantennerna även om du inte har en själv.Yes, geostationära satelliter har jag lite koll på från föreläsning om centralrörelse i rymden. De vill följa jordens rörelse och befinner sig runt ekvatorn. Men jag förstår fortfarande inte vad lösningsförslaget avser med och , och varför den observerade omloppstiden skiljer sig från den verkliga.
För en geostationär satellit är omloppstiden 24 timmar.
Den observerade omloppstiden är oändligt lång.
Pieter Kuiper skrev:coffeshot skrev:Pieter Kuiper skrev:Det finns geostationära satelliter, till exempel för TV.
Du har säkert sett parabolantennerna även om du inte har en själv.Yes, geostationära satelliter har jag lite koll på från föreläsning om centralrörelse i rymden. De vill följa jordens rörelse och befinner sig runt ekvatorn. Men jag förstår fortfarande inte vad lösningsförslaget avser med och , och varför den observerade omloppstiden skiljer sig från den verkliga.
För en geostationär satellit är omloppstiden 24 timmar.
Den observerade omloppstiden är oändligt lång.
I lösningsförslaget får man dock ett ändligt samband mellan de. Eller tänker jag fel?
Jaha, vänta, man ser alltid satelliten från jorden som att den är vid samma punkt hela tiden.
coffeshot skrev:Pieter Kuiper skrev:Den observerade omloppstiden är oändligt lång.
I lösningsförslaget får man dock ett ändligt samband mellan de. Eller tänker jag fel?
Det är en tolkningsfråga. Om satelliten stannar vid zenit, har vi då kanske?
Edit, nej, det stämmer inte heller med lösningsförslagets formler.
Pieter Kuiper skrev:coffeshot skrev:Pieter Kuiper skrev:Den observerade omloppstiden är oändligt lång.
I lösningsförslaget får man dock ett ändligt samband mellan de. Eller tänker jag fel?
Det är en tolkningsfråga. Om satelliten stannar vid zenit, har vi då kanske?
Edit, nej, det stämmer inte heller med lösningsförslagets formler.
Ja, det är lite spännande. Men det finns egentligen inget som säger att detta är en geostationär satellit väl, mer än att man kan ana det? Beroende på vad är så kommer den antingen vara geostationär eller inte. Om är den geostationär enligt Wikipedia.
coffeshot skrev:Men det finns egentligen inget som säger att detta är en geostationär satellit väl,
Det finns förstås andra också. Jag tog detta som exempel för att du skrev att du hade svårt att se hur dessa perioder kunde vara olika.
Jag tror att GPS (osv) har perioder på 12 timmar, men de ligger inte i ekvatoriala banor.
Space station (och mycket annat) ligger mycket lägre, perioder på typ 90 minuter.
Det kan du kolla formlerna med: https://eol.jsc.nasa.gov/Tools/orbitTutorial.htm
Pieter Kuiper skrev:coffeshot skrev:Men det finns egentligen inget som säger att detta är en geostationär satellit väl,
Det finns förstås andra också. Jag tog detta som exempel för att du skrev att du hade svårt att se hur dessa perioder kunde vara olika.
Jag tror att GPS (osv) har perioder på 12 timmar, men de ligger inte i ekvatoriala banor.
Space station (och mycket annat) ligger mycket lägre, perioder på typ 90 minuter.
Ah, jag förstår! Tusen tack för den insikten, nu hänger jag med på den biten! Jag är dock fortfarande som tidigare nämnt osäker på vad man gör i facit, vilket jag beskrivit ovan, se t.ex. #1/OP.
Kalla satellitens vinkelhastighet . Det skall då gälla att
PATENTERAMERA skrev:Kalla satellitens vinkelhastighet . Det skall då gälla att
Tack! Jag har funderat lite ytterligare på detta problem. Är en rimlig tolkning av ditt angivna samband, samt problemet i allmänhet följande:
Satelliten roterar runt jorden med
Om du står på jorden, som roterar med en vinkelhastighet , så kommer du uppleva att satelliten är ovanför dig som om den befann sig i punkten , medan den faktiskt är i . Det är den skillnaden man i facit kallar för . Hur kom du fram till ? Jag tänkte att jag hade det för några minuter sedan, men jag tänkter att
och kan inte riktigt få ihop det. Men kanske har jag bara stirrat alldeles för länge på denna uppgift vid det här laget.
Om du står på jorden så är satellitens vinkelhastighet relativt jorden.
Sett från jorden så har satelliten roterat ett varv, dvs 2, då .
PATENTERAMERA skrev:Om du står på jorden så är satellitens vinkelhastighet relativt jorden.
Sett från jorden så har satelliten roterat ett varv, dvs 2, då .
Tack, då hänger jag nog med. Jag hänger med på vad lösningsförslaget gör nu också. I lösningsförslaget finns med i uttrycket för . Hur kan man få med given ditt resonemang?
, enligt del 1) av lösningen.
PATENTERAMERA skrev:
, enligt del 1) av lösningen.
Tack, nu hänger jag med!
Halloj igen! Återvände till denna uppgift för att kolla att jag kom ihåg den.
Jag tyckte den var så himla knasig, jag kom fram till följande alternativa resonemang, tycker det låter enklare. Frågan är bara om det är rimligt?
Vi har
Kalla punkten observatorn ser satelliten i för . För cirkelrörelse gäller . Detta ger oss att i , när satelliten rört sig en liten sträcka har vi Vi har från uppgiften.
Är detta också ett rimligt tankesätt?
Beteckningarna jag hänvisar till är från lösningsförslaget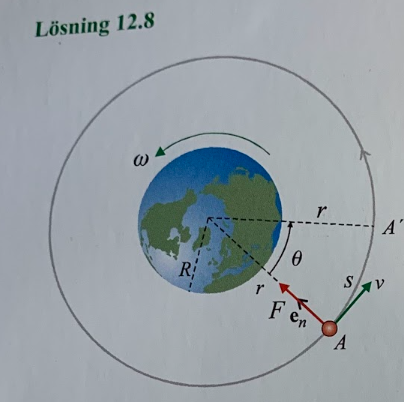
Först måste satelliten röra sig ett varv vilket motsvarar sträckan .
Men eftersom jorden snurrar så har observatören rört sig också, så för att komma i kapp observatören så måste satelliten röra sig ytterligare en sträcka s. Denna sträcka ges av , där är den vinkel som jorden har snurrat under tiden . Dvs .
Så satelliten skall röra sig sträckan . Eftersom satellitens hastighet är v så får vi
.
PATENTERAMERA skrev:Först måste satelliten röra sig ett varv vilket motsvarar sträckan .
Men eftersom jorden snurrar så har observatören rört sig också, så för att komma i kapp observatören så måste satelliten röra sig ytterligare en sträcka s. Denna sträcka ges av , där är den vinkel som jorden har snurrat under tiden . Dvs .
Så satelliten skall röra sig sträckan . Eftersom satellitens hastighet är v så får vi
.
Yes, okej, jag är on board för andra gången. Tack!



