Mekanik fjäder

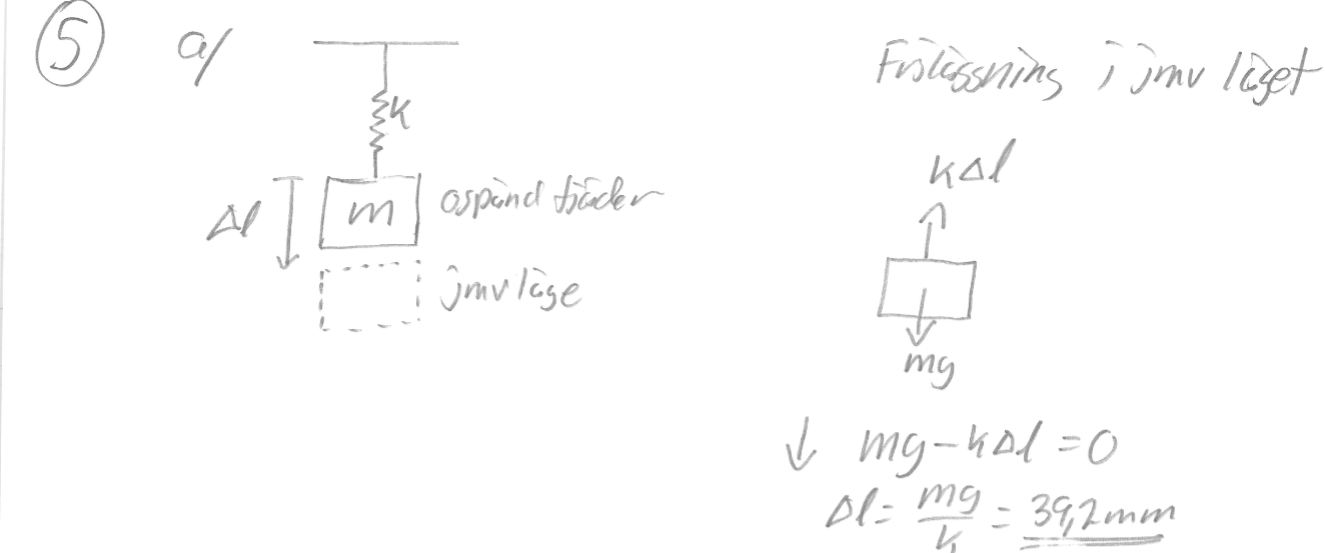
Aorta skrev:

Varför behöver en inte ta hänsyn till hastigheten i uppgift a?  

[...]

Jag undrar också vilket läge lösningsförslaget har räknat i. Är det det övre vändläget?

Nej. Som uppgiften säger: den statiska förlängningen. Alltså i jämviktsläget, där tyngden hänger stilla.

Okej. Kan en säga att det finns två jämviktslägen i vändlägena ("överst" och "underst") samt ett jämviktsläge där tyngden strävar efter att vara, alltså där den hade stannat efter att den hade svängt färdigt?

Jag tror att det gjorde mig förvirrad att det stod i uppgiften att tyngden hade en hastighet när tyngden passerar sitt jämviktsläge, men det är inte det jämviktsläget jag räknar på

Aorta skrev:

Kan en säga att det finns två jämviktslägen "överst" och "underst"  

Nej. Det är ju inte jämvikt.

Men hur kan den vara stilla om det inte är jämvikt?

I vändpunkten är hastigheten noll men den hänger inte stilla. Det är acceleration där.

Den är i jämvikt när rörelsen har dämpat ut. Då är det ett statiskt läge.

Tänk bara på gunga.

Jag tror att jag är med då! Tack för hjälpen. Jag har även en undran på uppgift b.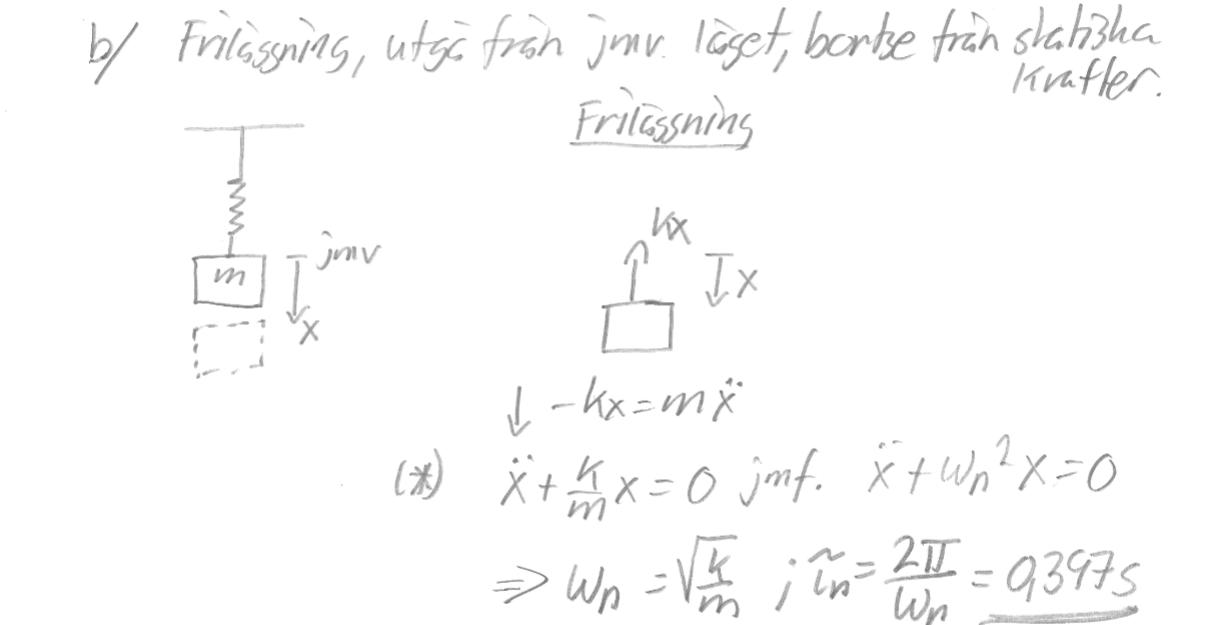

g är tyngdaccelerationen. Har de döpt om den till $\stackrel{..}{x}$eller är det någon total acceleration? Och varför har en i så fall bortsett från g? I friläggningen är inte g med vilket gör mig fundersam.

Aorta skrev:
Har de döpt om den till $\stackrel{..}{x}$eller är det någon total acceleration?  

Punktnotation kan användas för tidsderivator, så ${\ddot x} = {\dot v}$, tyngdens acceleration.

De bortser från statiska krafter. När jag undervisade om massan på en fjäder tog jag det alltid horisontellt. Det blir konceptuellt mycket enklare. Och det blir samma sak i slutet.

Är det för att gravitationen är konstant som en kan bortse från den? Att den är lika stor i jämviktsläget som i bottenläget

Aorta skrev:

Är det för att gravitationen är konstant som en kan bortse från den? Att den är lika stor i jämviktsläget som i bottenläget

Du kan förstås ta med gravitationen, det kan vara instruktivt att gå igenom hela algebran på det sättet. Och då behöver man till exempel anta att fjädern är linjär, alltså att den beter sig enligt Hookes lag (något som inte stämmer i verklighet).

Tack för hjälpen!