Mekanik: Ekorrhjul
Hej!
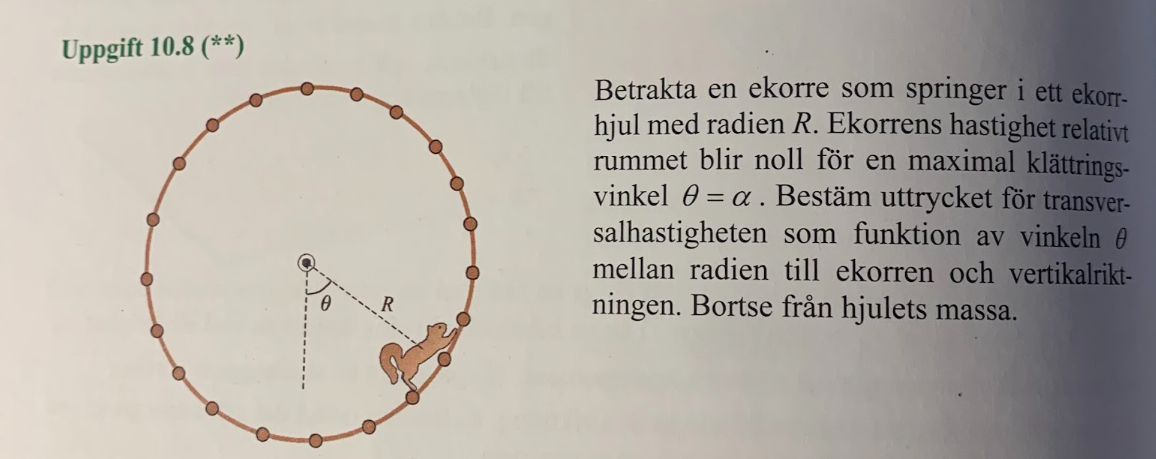
Jag försöker förstå detta lösningsförslag kring "ekorrhjulet", men jag är lite osäker på steget där uttrycket för tas fram.
Jag försöker hänga med på hur .
Är det för att man menar att ? Hur kan man se det isåfall? Jag förstår inte riktigt hur de tänker att -axeln är orienterad. Om axeln skulle vara orienterad utåt pappret/skärmen, stämmer det ju att kraften är ritad så att den är vinkelrät mot -axeln och därav bör den bidra . Men det känns inte intuitivt att ekorren skulle springa runt i -planet. Man har ritat så att den går i -riktningen, så man menar ju att ekorren inte springer runt i -planet, men jag kan helt enkelt inte se hur kommer in när man kollar på momentekvationen och rörelsemängdsmomentet.


coffeshot skrev:man menar att ? Hur kan man se det isåfall?
Ja, vridmomentet är runt ekorrhjulets axel.
Jag förstår inte riktigt hur de tänker att -axeln är orienterad. Om axeln skulle vara orienterad utåt pappret/skärmen, stämmer det ju att kraften är ritad så att den är vinkelrät mot -axeln och därav bör den bidra .
Exakt.
Men det känns inte intuitivt att ekorren skulle springa runt i -planet.
Ekorren rör sig inte i sidled (det som ekorren kallar "sidled") utan enbart längs själva ekorrhjulets kant. Den kanten går ju framåt-bakåt-upp-ner men inte i "sidled".
Man har ritat så att den går i -riktningen, så man menar ju att ekorren inte springer runt i -planet,
Tvärtom. Down är en riktning i xy-planet, vinkelrätt mot hjulets vridaxel (och den axeln är ju z-riktning)
men jag kan helt enkelt inte se hur kommer in när man kollar på momentekvationen och rörelsemängdsmomentet.
Det är tyngdkraftens komposant i tangentiell riktning.
Bubo skrev:coffeshot skrev:man menar att ? Hur kan man se det isåfall?
Ja, vridmomentet är runt ekorrhjulets axel.
Jag förstår inte riktigt hur de tänker att -axeln är orienterad. Om axeln skulle vara orienterad utåt pappret/skärmen, stämmer det ju att kraften är ritad så att den är vinkelrät mot -axeln och därav bör den bidra .
Exakt.
Men det känns inte intuitivt att ekorren skulle springa runt i -planet.
Ekorren rör sig inte i sidled (det som ekorren kallar "sidled") utan enbart längs själva ekorrhjulets kant. Den kanten går ju framåt-bakåt-upp-ner men inte i "sidled".
Man har ritat så att den går i -riktningen, så man menar ju att ekorren inte springer runt i -planet,
Tvärtom. Down är en riktning i xy-planet, vinkelrätt mot hjulets vridaxel (och den axeln är ju z-riktning)
men jag kan helt enkelt inte se hur kommer in när man kollar på momentekvationen och rörelsemängdsmomentet.
Det är tyngdkraftens komposant i tangentiell riktning.
Hmm, men det jag menar är att har man inte ritat så att den inte går längs med -axeln i lösningsförslaget? Eller tänker jag fel?

Läste mitt inlägg igen och kanske kan förtydliga det lite. Det jag menar är att som man ritat i bilden så är kraften vinkelrät mot -axeln om man avser -axeln som utåtriktad från pappret/skärmen. Men det stämmer inte eftersom då borde vara ritad så att den går längs med -axeln, vilket den inte är.
Jag tror att du tänker dig att ska vara riktad i samma plan som krafterna, men tänk på att z-komponenten av det här momentet är riktat rakt in i pappret.

Är du med på det? Detsamma gäller rörelsemängdsmomentet eller H eller vad ni nu kallar det.
D4NIEL skrev:Jag tror att du tänker dig att ska vara riktad i samma plan som krafterna, men tänk på att z-komponenten av det här momentet är riktat rakt in i pappret.
Är du med på det? Detsamma gäller rörelsemängdsmomentet eller H eller vad ni nu kallar det.
Jo det är jag med på, åtminstone algebratiskt. Det jag inte förstår är att gravitationskraften, , bör ju alltid peka i -led-tänker jag.
När man räknar på moment, så kan man räkna med (vinkelräta avstånden och kraftkomposanterna m.a.p. där man beräknar momentet). Som man uttryckt det i lösningsföslaget, är och . Dvs. man menar nog att axeln är riktad ut från skärmen (kan ha råkat skriva inåt i tidigare posts). Men jag begriper då inte varför man ritat tyngdkraften som att den skulle gå i -riktingen?
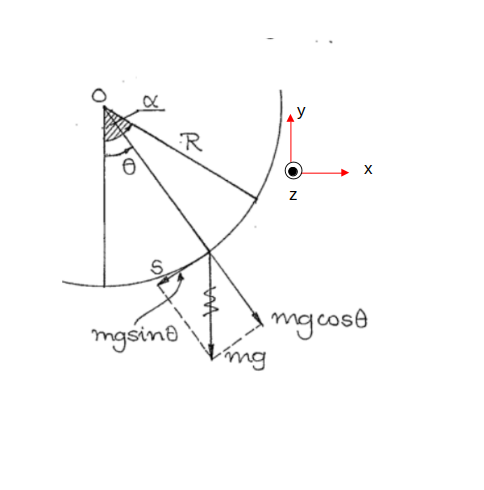
Förklarar detta min fråga lite tydligare?
Jag vet inte vad strecken som ritats ut vid -vektorn betyder, har aldrig sett det för övrigt. Vad menar man när man ritar så?
Neråt är -y i din senaste figur, x i D4NIELs figur.
z är ut ur pappret i din figur, in i pappret i D4NIELs figur.
De konstiga strecken I mg-vektorn har jag aldrig sett förut.
Inte jag heller, men en gissning kan väl vara att vektorn ersatts av de radiella/tangentiella komposanterna.
Bubo skrev:Neråt är -y i din senaste figur, x i D4NIELs figur.
z är ut ur pappret i din figur, in i pappret i D4NIELs figur.
Z in i pappret I bägge fallen, tror jag när jag tänker efter. Inte I pappret plan, I alla fall.
Vinkeln ska markeras från x-axeln och växa positivt mot y-axeln (moturs) i standardframställningen av polära-, respektive cylindriska koordinater.
Vidare använder vi uppräkningsordning och varför
Riktningen på är upp från pappret, mot oss.
Riktningen på är rakt in i pappret, i negativ -led. Tyngdkraften vill rotera systemet medurs på bilden.
Man får naturligtvis lägga sina koordinatsystem hur man vill, men om man ska använda standarduttrycken samt få rätt tecken i kryssprodukter, determinanter och dylikt bör man utgå från "standardkoordinater", dvs ett ortonormerat högersystem.
I standarduppställningen är alltså tyngdkraften på bilden från facit riktad i positiv x-led.
D4NIEL skrev:Vinkeln ska markeras från x-axeln och växa positivt mot y-axeln (moturs) i standardframställningen av polära-, respektive cylindriska koordinater.
Vidare använder vi uppräkningsordning och varför
Riktningen på är upp från pappret, mot oss.
Riktningen på är rakt in i pappret, i negativ -led. Tyngdkraften vill rotera systemet medurs på bilden.
Man får naturligtvis lägga sina koordinatsystem hur man vill, men om man ska använda standarduttrycken samt få rätt tecken i kryssprodukter, determinanter och dylikt bör man utgå från "standardkoordinater", dvs ett ortonormerat högersystem.
I standarduppställningen är alltså tyngdkraften på bilden från facit riktad i positiv x-led.
Hmm, okej. Bara så vi är på samma sida, vem är det som definierat koordinatsystemet tokigt? Det jag ritat på screenshoten borde väl följa ett högerorienterat system om jag inte misstar mig? Man brukar ju tänka sig att är riktad i -led, så är det facits koordinatsystemsval som är konstigt då?
Ja, det är kanske lite ovanligt att z inte pekar neråt. Å andra sidan kan man då kalla det intressanta planet (hjulet sett från sidan) för xy-planet.
Som Bubo påpekar är det koordinaterna i det intressanta planet som spelar roll.
Normalt sett brukar man definiera polära koordinater som
I vårt fall är det hamstern som ska röra sig i en cirkel. Därför är det naturligt att använda xy-planet till det.
Visst kan man låta x- och y-axlarna peka åt höger respektive uppåt som du gör i din bild. Men då tillkommer en vinkelförskjutning på för att få att fungera som i figuren.
För att slippa det är det enklare att bara rotera systemet så det passar med definitionen av i bilden.
Vill man låta vara "höjden" över marken i bilden kan man låta hamstern springa omkring i -planet. Men det kräver återigen en permutation av standarduppställningen och en fasförskjutning .
Och det tycker åtminstone jag är krångligare eftersom standarduttryck för alla nabla-operatorer måste räknas om, transformationsmatriserna måste permuteras och så vidare.
Som tillägg till D4NIELs fina förklaring kan det helt enkelt vara lika bra att vänja sig vid "ovanliga" koordinatsystem redan nu. Antagligen kommer du strax till den delen av mekanik där flera olika koordinatsystem roterar och flyger runt i tre dimensioner.
Tack för förklaringen! Jag tror jag förstår det hela bättre nu.
Bara för att dubbelkolla att jag förstått det hela, har vi här tänkt att tyngdkraften här är definierad i -led?
I D4NIELs inlägg nr 5 är tyngdkraften riktad i x-led.
I ditt inlägg nr 6 är tyngdkraften riktad I negativ y-led.
Bubo skrev:I D4NIELs inlägg nr 5 är tyngdkraften riktad i x-led.
I ditt inlägg nr 6 är tyngdkraften riktad I negativ y-led.
Superb, tack! Hänger med nu.


