Mekanik: Centralrörelse

Skulle gissa på att det är pga att vi enbart känner till hastighetens belopp, och inte riktning.

Notera att vi av detta inte kan beräkna rörelsemängdens belopp eftersom en kryssprodukt ingår i formeln, därmed behöver vi även hastighetens riktning.

Calle_K skrev:

Skulle gissa på att det är pga att vi enbart känner till hastighetens belopp, och inte riktning.

Notera att vi av detta inte kan beräkna rörelsemängdens belopp eftersom en kryssprodukt ingår i formeln, därmed behöver vi även hastighetens riktning.

Visst menar du rörelsemängdsmomentet?

Ja

Calle_K skrev:

Ja

Okej, bra! En fråga om varför beloppet av rörelsemängdsmomentet inte kan beräknas, så jag förstått det rätt bara. Anledningen till detta inte kan beräknas är att den ibland är riktad i $-\hat e_t$ riktningen och ibland i $+\hat e_t$-riktningen? Jag tänker att beloppet av rörelsemängdsmomentet alltid kommer vara konstant under centralrörelse, det är det jag har uppfattat från föreläsningar och liknande. Kan man inte beräkna det då?

Du kan ju sätta upp formlerna för E och L och se vilka du kan beräkna med endast vetskap om v och r.

Tex

E = $-\frac{GmM}{r}+\frac{1}{2}m{v}^2$, ja det ser ut att funka.

L_z = $m{r}^2\dot{\theta }$, kan vi lista ut värdet på $\dot{\theta }$endast med vetskap om v och r?

PATENTERAMERA skrev:

Du kan ju sätta upp formlerna för E och L och se vilka du kan beräkna med endast vetskap om v och r.

Tex

E = $-\frac{GmM}{r}+\frac{1}{2}m{v}^2$, ja det ser ut att funka.

L_z = $m{r}^2\dot{\theta }$, kan vi lista ut värdet på $\dot{\theta }$endast med vetskap om v och r?

Jag tolkar det som är hastigheten alltid är tangentiellt riktad i cirkelrörelse, så den är väl alltid vinkelrät mot $z$-axeln och således är $\left|L_z\right|=mv$?

Det står ingenting om cirkelrörelse i problemet.

Banan är elliptisk, hade det varit cirkelrörelse hade vi vetat riktningen på hastigheten.

PATENTERAMERA skrev:

Det står ingenting om cirkelrörelse i problemet.

Jag menar centralrörelse, sorry.

Då är det som jag säger att L_z = $m{r}^2\dot{\theta }$. Notera att mv inte ens har rätt dimension (rörelsemängd inte rörelsemängdsmoment).

PATENTERAMERA skrev:

Då är det som jag säger att L_z = $m{r}^2\dot{\theta }$. Notera att mv inte ens har rätt dimension (rörelsemängd inte rörelsemängdsmoment).

Jag menade $mrv$, förlåt om jag varit lite virrig de senaste inläggen i denna tråd.

Det jag hakade upp mig på var nog att $\vec H_O=\text{konst}$ vid centralrörelse. Rörelsemängdsmomentet ges av $mr^2 \dot theta$ som du säger. Jag tänkte att om vi vet $v$ och $r$ enligt uppgiften kan vi få fram rörelsemängdsmomentets belopp, eftersom jag tänkte att $v$ och $r$ alltid var vinkelräta mot varandra vid centralrörelse.

Jag tror jag förvirrade det hela lite: vid en perfekt cirkelrörelse med jorden i mitten skulle således vara fallet, och i apogeum och perrigeum (vid rörelse kring jorden) är $\vec r\perp \vec v$ även vid ellipsrörelse och då borde man således kunna få fram rörelsemängdsmomentets belopp om man hade vetat hastigheten och radien just där, korrekt?

Alltså, av någon lustig anledning tänkte jag att radien alltid var vinkelrät mot hastigheten, inte bara i specialfallen ovan. Jag ritade denna principskiss för rörelse kring godtycklig himlakropp där de röda vektorerna indikerar hastighetens riktning. Själva hastighetsbeloppet är inte skalenligt på något vis.

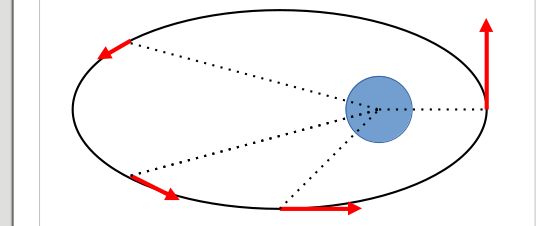
Nu inser jag hur tokigt tänkt det var av mig att radievektorn alltid är virkelrät mot hastigheten! Låter det jag kommit fram till nu rimligt?

Jag tolkar två tummar upp som att jag tänkt rätt och markerar tråden som löst, nöjd med hjälpen!