Mekanik. Balkuppgift. Beräkna M(x) och V(x) från punkten B till personen.

Jag tror att det är mycket lättare än du tror. Du behöver bara titta på delen till höger om B. D.v.s. snitta till höger om B, precis som du har gjort. Reaktionskrafterna vid stöden behöver du inte bry dig om. 

I din friläggning av högerdelen ska mg vara placerad längst till höger. V(x) vid snittytan måste vara motriktad mg för att jämvikt ska råda. D.v.s. antingen ritar du den uppåt eller byter du tecken i ditt uttryck "V(x)=mg" -> V(x)=-mg.

Annars tycker jag att du har en bra känsla. 

... eftersom momentet vid A kanske inte är 0 då det ej är en fri ände?

Helt korrekt. Momentet är inte 0 vid A. Men det behöver vi inte bry oss om för att lösa uppgiften. 

Jag tror att man ska göra olika "snitt"...

Helt korrekt. Man lägger precis det snitt som du gjorde (behöver inga andra snitt). Med det snittet löser du både tvärkraften V och momentet M. Kraft- och momentjämvikt på balkelementet gäller eftersom elementet inte rör sig. Hur resten av balken påverkar elementet sammanfattas av en tvärkraft, V, och ett böjmoment, M.

... före och efter momentet verkade och fick en  formel för balken före och en formel för balken efter momentet. Ska man göra något liknande här? 

Se ovan, behövs bara det snitt som du gjort. 

Jag satte xs som x-koordinaten för den högra änden av balken

Den kan du göra men i uppgiften har de åtminstone antytt att x=0 vid A och x=b längst till höger. Och de vill ha momentet uttryckt I bl.a. b. 

Om du läser denna så kanske du ser att det inte är så komplicerat egentligen:

https://ludu.co/course/hallf/snittning/

Hej! Stort tack för svar. Jag skulle bara vilja ställa några frågor, är inte helt klok på uppgiften än.

Jag förstår inte riktigt varför mg ska vara placerad längst till höger i min friläggning, eftersom personen inte står precis vid änden så borde väl det inte finnas några krafter vid den fria änden? Räcker det med att bara ändra riktning på V(x) och inte flytta mg?

Jag förstår inte riktigt heller hur jag kan beräkna M(x) med mitt snitt. Jag tycker liksom inte att jag har något att räkna på där. För mig verkar det som att M(x) måste vara 0 där för momentjämviktens skull? Jag får det till det här jag:

Jag läste informationen på hemsidan. Stort tack för den infon. Men i den här uppgiften förstår jag inte riktigt hur jag ska tillämpa det, då de efterfrågar M(x) från B till just personen. Betyder inte det att jag varken kan snitta före eller efter personen eftersom de vill ha M(x) från B till precis personen?

Stort tack.

Jag kanske missförstod var du la ditt snitt. Snittet ska vara mellan B och x=b (om du sätter x=0 vid A).

...varför mg ska vara placerad längst till höger i min friläggning, eftersom personen inte står precis vid änden...

Det har du rätt i. Personen står vid x=b och sedan fortsätter trampolinen en bit till. Den biten påverkar inget och är inte utsatt för spänningar. 

Jag tycker att ditt 1:a snitt i första inlägget (även "snitt av högeränden" i ditt senaste inlägg) är bra om du bara flyttar mg så att mg inte ligger i snittet (d.v.s. snitta mellan B och x=b). Då får mg en hävarm (räkna moment kring snittpunkten).

I länken tänkte jag att detta är likt din situation. De har valt x-riktning åt andra hållet och kraften är riktad åt andra hållet men annars är det samma, tycker jag.  

Hej! Stort tack för svar igen. 

Jag försökte snitta mellan B och x = b så att mg inte kom med i snittet. Då fick V(x)=mg hävarmen (x-a) och så försökte jag räkna momentet med avseende på B, men då fick jag ett svar i termer av x, mg och b, men det rätta svaret ska uttryckas i termer av x, b och mg. Så jag har nog fortfarande inte förstått riktigt. Var går det snett?

Nu förstår jag inte vad du försöker göra, tror jag. 

Det som hjälper dig framåt är att göra ett snitt vid x, där x>a och x<b. Sedan tittar du på den högra delen av trampolinen. Där kommer mg att finnas vid x=b. Det kommer inte att finnas något internt böjmoment M vid x=b. Vid x, d.v.s. där du har snittat kommer det att finnas en tvärkraft V(x) och ett internt böjande moment M(x). Dessa 2 storheter representerar hur den vänstra delen av trampolinen påverkar den högra. Genom att snitta har vi alltså frilagt en del av trampolinen, d.v.s. vi har ersatt resten av trampolinen med ett M och ett V.

Nästa steg är att sätta upp kraft- och momentjämviktsekvationer. Kraft har du redan löst och kommit fram till att V(x)=mg för x>a och x<b och att den är uppåtriktad. När det gäller momentet så är det lämpligt att beräkna moment kring snittet vid x. Vilken hävarm får då mg?

Stort tack för svar!

Jag ska läsa igenom det och försöka igen. Jag kommer kanske inte att försöka på några dagar då jag har tenta i linjär algebra om några få dagar bara som jag måste fokusera på, så jag har inte övergett tråden bara för att jag inte skriver något på några dagar så att du vet!

Hej! Nu har jag försökt igen och får fram rätt svar, M(x) = -mg(b-x) genom att göra som du sagt.

Först fick jag mg(b-x) vilket var fel men när jag testade med att lägga till ett minustecken blev det rätt..Jag antar att det är för att böjmomentet vid den vänstra delen av a<x<b ska vara motriktat böjmomentet vid snittet vid x, alltså den högra delen av a<x<b.

Men jag förstår knappt vad jag egentligen gör för något..

Hur inser man att det inte finns något internt böjmoment vid x = b? Hur vet man att de två storheterna representerar hur den vänstra delen påverkar den högra?

Hur förstår man att V(x) = mg överallt i balken och inte bara vid x = b?

Stort tack.

Delarna av balken som hänger ut

Allt till vänster om stödet vid A och till höger om personen kan du rationalisera bort i modellen. Dessa delar av balken kommer vara spänningsfria (de är spänningsfria för att det inte finns något internt motstånd mot deformation och därmed fri rörelse, försök böja en banan eller pinne och jämför själv). Dessa områden är markerade i grått nedan:

Initial kraftjämvikt för att bestämma reaktionslaster

Vi kan bara för sakens skull bestämma de okända reaktionslasterna vid A och B:

Interna reaktioner, tvärkraft och moment

Det enklaste sättet att ta fram moment och tvärkraft som funktion av balkens längd är att göra ett s.k. positivt högersnitt. Vi kan göra det i båda delar av balken (punktkrafter och moment skapar diskontinuiteter och således olika ekvationer). 

Snitt i vänstra delen av balken

För $x$ från vänstra änden för $0<x<a$ får vi:

Du ser att koordinaten $x$ löper alltså från punkten A till snittet. En bra kontroll av snittstorheter är att derivatan av momentekvationen ska vara lika med tvärkraften vilket vi ser stämmer här eftersom:

$\dfrac{dM (x)}{dx}=-R_A = V\left(x\right)$ 

Snitt i högra delen av balken

För $x$ i andra delen, alltså $a<x<b$ får vi:

Eftersom vi vet att $R_A + R_B = mg$ får vi:

$V(x) = -mg$ 

$M(x) = mg(b-x)$

Där vi valt konventionen att tvärkraften är uppåt och momentet medurs vid ett positivt snitt.

Varför negativt svar?

Som du ser fick vi ett negativt svar på både $V(x)$ och $M(x)$ till skillnad från det "rätta svaret". Detta är för att din föreläsare valt en annan konvention där snittet istället har en tvärkraft som pekar nedåt och ett moment som är moturs. Detta är typiskt den amerikanska konventionen, inte den svenska:

Sammanfattning

Jag kunde svarat på varje individuell fråga men det blev så många och jag förstår inte riktigt vissa av dem så jag tänker att det var bäst att bara gå igenom så många av grunderna som möjligt från början till slut. Notera att första snittet var onödigt eftersom vi inte bryr oss om tvärkrafter och moment då $0<x<a$.

För att visualisera sitt resultat kan man konstruera diagram för tvärkrafter och moment enligt nedan:

Tusen tack!

Hur kan M(x) blir växande fram till a i grafen när du beräknat den till -RAx som är negativ? 

Som sig bör är $R_A$ negativ (nedåtriktad) så momentet blir positivt $M(x) = mg(b/a-1)x$.

SaintVenant skrev:

Delarna av balken som hänger ut

Allt till vänster om stödet...

Snyggt SaintVenant!

Peter skrev:

SaintVenant skrev:

Delarna av balken som hänger ut

Allt till vänster om stödet...

Snyggt SaintVenant!

Håller med. Ett fantastiskt inlägg. 

Jag undrar övrigt om detta brukar vara den lättaste metoden, alltså att snitta sig fram från x=0 i varje del där det dykt upp en intressant kraft. Ett positivt högersnitt antar jag att det endast blir i den svenska konventionen. På tal om konvention, vad är det som gör att snittet blir korrekt? 

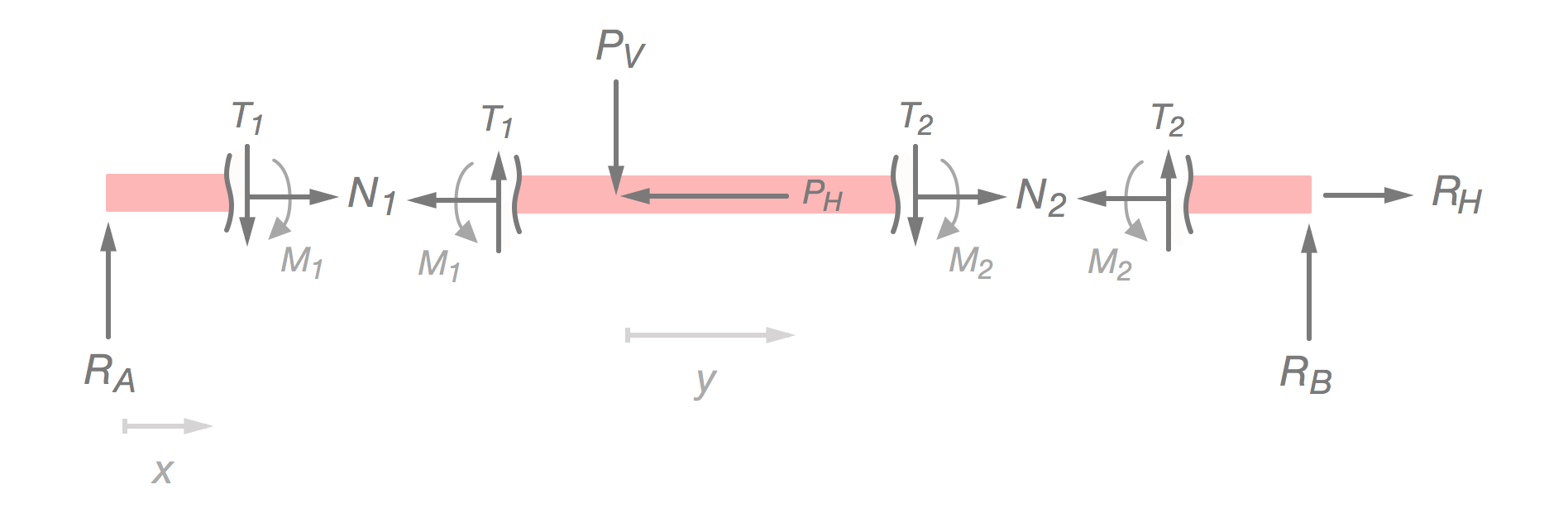
Är kravet helt enkelt att man har moment och krafter som är motriktade, eller måste också kraften vid medurs moment alltid vara uppåtriktad och kraften vid moturs moment alltid vara nedåtriktad? För det märker jag är samma för båda konventioner.  Varför är det så? För momenten tycker jag det är logiskt att se att balken böjs nedåt som en glad mun (för amerikansk konvention) men kraftriktningarna känns väldigt random. 

Jag undrar övrigt om detta brukar vara den lättaste metoden, alltså att snitta sig fram från x=0 i varje del där det dykt upp en intressant kraft.

 Ja, så skulle jag nog säga att man gör.

Är kravet helt enkelt att man har moment och krafter som är motriktade, eller måste också kraften vid medurs moment alltid vara uppåtriktad och kraften vid moturs moment alltid vara nedåtriktad?

Nej, du är fri att välja positiva riktningar hur du vill. Positiva "kraftriktningen" hänger inte ihop med positiva momentriktningen. Du kan välja fritt men du måste vara konsekvent för de ekvationer som hänger ihop (de ekvationer som beskriver samma balkelement). Däremot behöver du inte vara konsekvent mellan olika element. Det går bra att byta positiva riktningar mellan beräkningarna av vänstra trampolinen och den högra men det kan ju bli lite rörigt. 

MrPotatohead skrev:
Jag undrar övrigt om detta brukar vara den lättaste metoden, alltså att snitta sig fram från x=0 i varje del där det dykt upp en intressant kraft.

Ett negativt vänstersnitt är bäst i detta fall då man inte bryr sig om $0<x<a$ men jag ville inte överösa frågeställaren med information. Å andra sidan är det kanske ett negativt vänstersnitt som uppgiftskonstruktören förväntar sig att man ska göra eftersom man får svaren direkt utan friläggning och kraftjämvikt:

Ett positivt högersnitt antar jag att det endast blir i den svenska konventionen. 

Det är ett positivt snitt i båda konventioner då normalvektorn till snittet är till höger, vilket blir samma riktning som koordinaten längs med balken, då blir alla snittstorheter positiva i snittets koordinatsystem. Det blir normalens riktning relativt en tänkt koordinataxel som avgör namngivning.

Sedan roterar man helt enkelt koordinatsystemet runt normalvektorn för att konstruera de olika snittstorheterna:

Här ser du att både moment och tvärkraft är i positiv riktning för sina respektive axlar i både svensk och amerikansk konvention.

På tal om konvention, vad är det som gör att snittet blir korrekt? Är kravet helt enkelt att man har moment och krafter som är motriktade, eller måste också kraften vid medurs moment alltid vara uppåtriktad och kraften vid moturs moment alltid vara nedåtriktad? För det märker jag är samma för båda konventioner.  Varför är det så? För momenten tycker jag det är logiskt att se att balken böjs nedåt som en glad mun (för amerikansk konvention) men kraftriktningarna känns väldigt random. 

Man pratar väl egentligen mer om att de ska vara i positiv riktning för snittytan. Har man x i normalriktning, y i djupled och z i tvärled så är det inte lika "snyggt" om momentet är i positivt y-led men tvärkraften i negativt z-led. Sedan är nedan samband från jämvikt något som gäller för både svenska och amerikanska:

$\dfrac{dM(x)}{dx} = V\left(x\right)$

Med följande relation till lastintensitet $q$:

$\dfrac{dV\left(x\right)}{dx}=-q$

Hur konventionen är vald har sedan att göra med om det är uppböjning eller nedböjning som antas som positiv för en godtycklig balk i böjning (således även lastintensiteten $q$:s riktning):

Man har formulerat en differentialekvation för balken, påtvingat vissa Bernoulli-villkor och löst den. Men egentligen är det ju bara mekanik så du kan göra vilken friläggning du vill. Är problemet statiskt bestämt kommer de korrekta riktningarna ramla ut av sig själv.

Problem dyker upp om systemet är statiskt obestämt. Då måste du plötsligt förlita dig på kompatibilitet, deformationssamband, elementarfall osv. och då blir det väldigt, väldigt lätt att göra fel om man inte håller sig till konsekventa samband med ursprung i entydig definition av elastiska linjens ekvation.

På tal om konvention, vad är det som gör att snittet blir korrekt?

För klassisk hållfasthetslära och snittning, om snittstorheter har riktningen som i bilden du hittat ovan så ändrar du definitionen av jämviktsekvationerna jag skrev tidigare. Du byter tecken på differential-sambandet från jämvikt mellan moment och tvärkraft samt mellan tvärkraft och lastintensitet så att det blir:

$\dfrac{dM(x)}{dx} = -V\left(x\right)$

$\dfrac{dV(x)}{dx} = q$

Sedan har du också antingen momentet eller tvärkraften i negativ riktning för ett högerhands-system på snittet. Se nedan och jämför med tidigare:

Här ovan har vi alltså att någon av tvärkraft eller moment alltid är negativ oavsett hur man roterar koordinatsystemet runt x-axeln.

Det vi ser i din bild tror jag är typiskt FEM-konvention, om jag minns rätt. Då löser man väl virtuella arbetets princip på svag form för olika balkelement lokalt och det blir skitsamma vilken konvention man använder eftersom transformation av matriser är så enkel.

Men, kring de här mest intrikata detaljerna är jag dock ute på lite djupt vatten, tyvärr.

Du har hämtat bilden från ludo.co och jag tror helt enkelt att Pierre Lindgren missat konventionen och varför den kan vara viktig för vissa sammanhang. Alla problem han går igenom är mycket enkla och då uppstår inte problemen.

Peter skrev:
Däremot behöver du inte vara konsekvent mellan olika element. Det går bra att byta positiva riktningar mellan beräkningarna av vänstra trampolinen och den högra men det kan ju bli lite rörigt. 

I princip, ja, men vill man konstruera diagram eller på annat sätt relatera koordinatberoende hos elementen mellan varandra måste du vara konsekvent i val av konvention. Annars kommer du till exempel i detta fall för svensk konvention ha positivt moment för $0<x<a$ och för amerikansk konvention ett negativt moment för $a<x<b$, med en diskontinuitet vid a, se nedan:

Men som du skriver, har man tungan rätt i mun så är det görbart, absolut.

Tillägg: 11 jan 2025 19:40

Jag försökte svara så uttömmande jag kunde, men tyvärr krävdes en del spekulationer och antaganden. Hoppas det hjälper ändå!

Detta var förövrigt mitt sista inlägg på Pluggakuten.se.

Tack för mig!

Stort tack för all hjälp!

Tråkigt att höra SaintVenant. Dina kunskaper är ovärderliga här. Tack för ett välutvecklat och bra inlägg och lycka till med dina andra planer i livet.😎