Mekanik 2 upg 1.29
jag skulle behöva hjälp med hur man löser denna uppgift, var börjar man?
@Maja9999, variera dina trådrubriker för att du själv och de som hjälper dig ska kunna särskilja dem. Det bästa är om du lyckas koppla rubriken specifikt till uppgiften, annars fungerar simpel numrering. /Moderator
Mrpotatohead skrev:koppla rubriken specifikt till uppgiften
Ett tips till alla trådstartare!
Försök fånga vårt intresse med rubriken. (Men inte klickbait, förstås.)
Den här uppgiften är ekvivalent med att studera en vikt som hänger i en fjäder under inverkan av gravitationen . Partikeln kommer börja utföra en harmonisk svängning kring systemets jämviktspunkt.
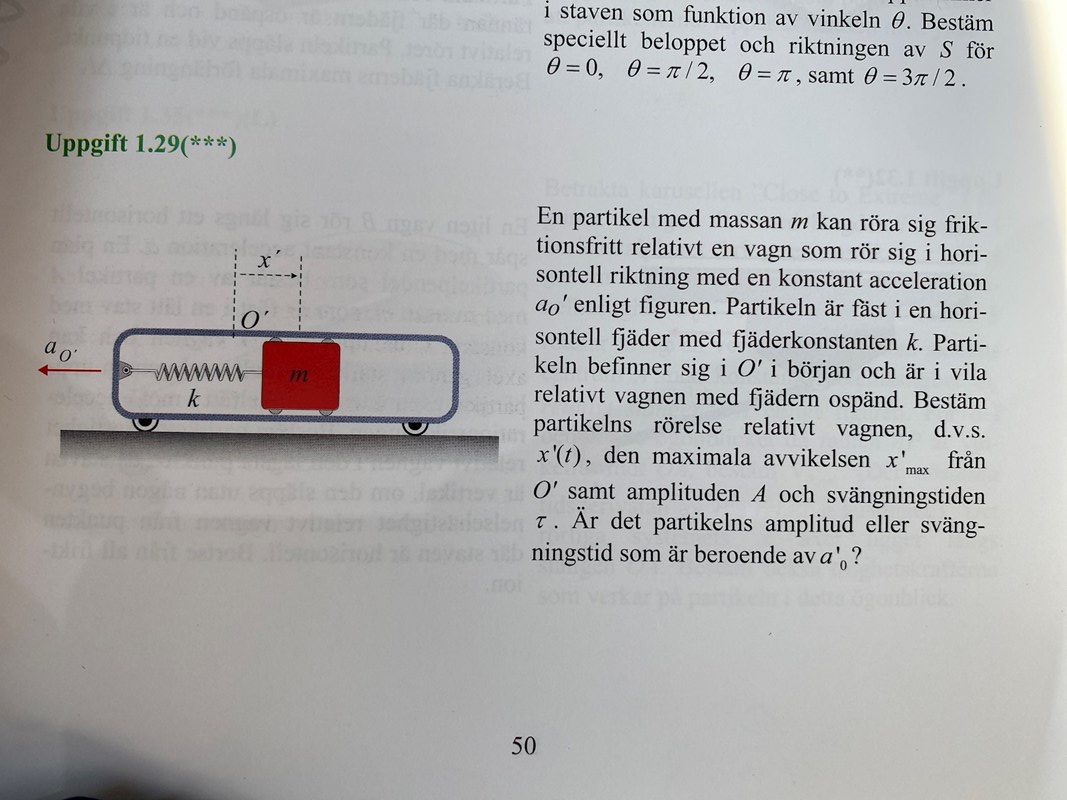
En bra början är att snitta och frilägga vikten i koordinatsystemet samt märka ut krafterna som verkar på den. Det enda som är "ovanligt" är att du får en tröghetskraft (fiktiv kraft). När du märkt ut krafterna kan du räkna precis som du gjorde när du löste problemet med en vikt som släpps en bit ovanför jämviktsläget hängande i en fjäder i grundkursen. Om du är lat kan du använda formlerna och sambanden från den harmoniska oscillatorn.
Visa dina försök om du fastnar, lycka till.
D4NIEL skrev:Den här uppgiften är ekvivalent med att studera en vikt som hänger i en fjäder under inverkan av gravitationen . Partikeln kommer börja utföra en harmonisk svängning kring systemets jämviktspunkt.
En bra början är att snitta och frilägga vikten i koordinatsystemet samt märka ut krafterna som verkar på den. Det enda som är "ovanligt" är att du får en tröghetskraft (fiktiv kraft). När du märkt ut krafterna kan du räkna precis som du gjorde när du löste problemet med en vikt som släpps en bit ovanför jämviktsläget hängande i en fjäder i grundkursen. Om du är lat kan du använda formlerna och sambanden från den harmoniska oscillatorn.
Visa dina försök om du fastnar, lycka till.
 Såhär långt har jag kommit nu. Men jag får inget tidsberoende x’?
Såhär långt har jag kommit nu. Men jag får inget tidsberoende x’?
marel = F + Fsp + Fcor = (-kx’ + maO’)ex’
arel = (d2x’/dt2)ex’.
PATENTERAMERA skrev:marel = F + Fsp + Fcor = (-kx’ + maO’)ex’
arel = (d2x’/dt2)ex’.
Hur får du fram arel = (d2x’/dt2)ex’
Det är accelerationen relativt det rörliga systemet. Säg att du åker med vagnen. Vilken acceleration relativt dig och vagnen skulle du anse att partikeln har?
PATENTERAMERA skrev:Det är accelerationen relativt det rörliga systemet. Säg att du åker med vagnen. Vilken acceleration relativt dig och vagnen skulle du anse att partikeln har?
Aha det där är alltså bara dubbel tidsderivata av x? Alltså x prick prick?
Ja, precis.




