Medelvärde och standardavvikelse
En fabrik producerar golfbollar. Golfbollarnas diameter kan antas vara
normalfördelad.
Ungefär 12 % av bollarna har en diameter lägre än 41,9 mm och 20 % av bollarna har
en diameter över 43,5 mm.
Bestäm medelvärdet och standardavvikelsen för bollarnas diameter
Jag antar att diametern på bollarna placeras ut på x-axeln. 12% är den som är 13,6% på diagrammet. Vet inte hur jag ska gå till väga.
Men det kan inte ligga symmetriskt så, för den nedre vänstra ska vara 12% och den övre vita 20%, inte 16% var.
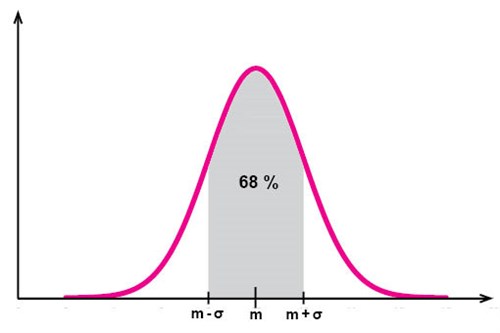
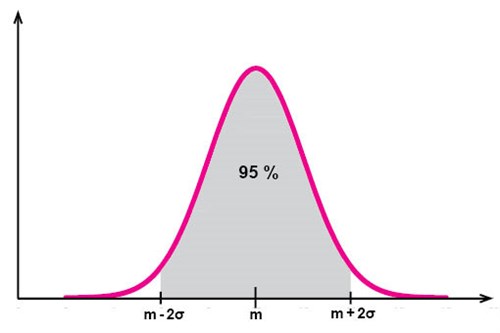
Jag är lite osäker på hur pass exakt man kan lösa den här uppgiften inom ramen för Matte 2. Hos en normalfördelning är 50 % av värdena lägre än medelvärdet, medan ungefär 16 % är mindre än medelvärdet minus 1 standardavvikelse. Runt 2,5 % är mindre än medelvärdet minus 2 standardavvikelser.
41,9 mm måste alltså ligga mellan 1 och 2 standardavvikelser från medelvärdet. 43,5 mm måste ligga mellan medelvärdet och medelvärdet plus 1 standardavvikelse.
Men moderator, nu "redigerade du sönder" tråden så mitt svar inte går att begripa :-)
Om frågeställaren har en tabell över normalfördelningen så går ju den att använda. Får man bara lära sig procenttalen för en och två standardavvikelser så går det förstås inte.
Laguna skrev:Men moderator, nu "redigerade du sönder" tråden så mitt svar inte går att begripa :-)
Om frågeställaren har en tabell över normalfördelningen så går ju den att använda. Får man bara lära sig procenttalen för en och två standardavvikelser så går det förstås inte.
Sorry! Jag måste ha ändrat svaret samtidigt som du postade ditt. Såg din kommentar när jag uppdaterade sidan igen. Du var nästan snabbare än jag på att posta ditt svar :)
Jag insåg samma sak som du...
Den enda approachen jag ser är att man måste ta reda på vilket värde som har 12% respektive 80% (1-20%) till vänster om sig i en tabell över normalfördelningens CDF, alternativt en funktion som räknar ut det.
Låt oss säga att man med en sån referens hittar att vid värdet X har man 12% av en standardnormalfördelning till vänster (dvs CDF(X) = 0.12) och vid värdet Y har man 20% till höger, dvs 80% till vänster (CDF(Y) = 0.80). Då kan man använda omskalningen av vår faktiska fördelning av golfbollar för att få
De här två ekvationerna kan man sedan lösa på vanligt sätt för att få fram och .
Fofafobianon: jag insåg precis att mitt svar kanske inte är helt lätt att smälta när man precis börjat kolla på de här sakerna, men vi kan ta det steg för steg också. Första steget är att lista ut vilket värde i en vanlig normalfördelning, alltså en med medelvärde 0 och standardavvikelse 1, som har 12% av fördelningen till vänster om sig. Sedan gör man samma sak för att hitta 80%-gränsen.
Det jag kallar för CDF är "cumulative density funktion", som jag antar heter något i stil med "kumulativ normalfördelning" på svenska. Om man hade en dator med alla funktioner kan jag tänka mig att det man helst vill använda är "CDF invers" eller "CDF^-1", eftersom man istället för det vanliga "hur många procent av fördelningen ligger till vänster om X?" nu vill räkna ut "vilket X har 12 procent av fördelningen till vänster om sig?".
Det kan mycket väl hända att det finns tabeller i din statistikbok som man kan kolla upp ungefärliga siffror i också!
Varifrån kommer uppgiften? Varför tror du att den passar i Ma2?
Problemet har varit uppe nyligen
https://www.pluggakuten.se/trad/berakna-medelvardet-och-standardavvikelse/
Kanske bilden kan ge ledning till källan?




