Medelkraft på en elektron i cirkelrörelse i ett magnetiskt fält

Hej. Frågan är:

"Ett homogent vertikalt magnetfält har ett rektangulärt tvärsnitt PQRS, se figur:"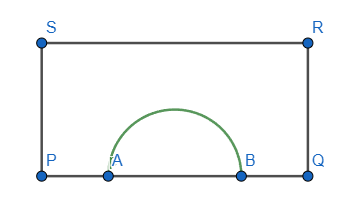

(halvdålig återskapelse av figuren)

"En horisontell ström av elektroner kommer in i fältet vid A, vinkelrätt mot PQ med farten $6.2$ Mm/s.
De böjs och lämnar åter fältet vinkelrätt mot PQ vid B. Avståndet AB är $0.120$ m. Elektronstrålen befinner sig hela tiden i vakuum. Bortse från jordmagnetiska fältet och gravitationen."

b-uppgiften är följande:
"Hur stor medelkraft vinkelrätt mot PQ verkar på elektronerna under den tid de rör sig i magnetfältet?"

Min lösning: 
Kraften som verkar vinkelrätt mot PQ blir $F \sin{\alpha}$, där $F$ är den magnetiska kraften och $\alpha$ är vinkeln som elektronen gör med mittpunkten på halvcirkeln. Om man då vill ha en approximation på medelkraften kan man välja ut $n$ vinklar och beräkna dessa värden och sedan dela summan med antalet termer, $n$. Alltså får man att 
$\displaystyle F_{medel} \approx \frac 1n \sum_{k=0}^{n}{F\sin{\left(\frac{\pi k}{n}\right)}}$
Låter man antalet vinklar gå mot oändlighet får man då en likhet
$\displaystyle F_{medel} = \lim_{n \to \infty} \frac{F}{n} \sum_{k=0}^{n}{\sin{\left(\frac{\pi k}{n}\right)}}$ $\displaystyle = F \lim_{n \to \infty} \sum_{k=0}^{n}{\sin{\left(\frac{\pi k}{n}\right)} \frac 1n}$
Om vi multiplicerar in $\pi$ i summan blir det en riemannsumma av $\displaystyle \int\limits_0^\pi{\sin{x}\, dx}$
Därför är $\displaystyle F_{medel} = \frac F\pi \int\limits_0^\pi{\sin{x}\, dx} = \frac{2F}{\pi}$
Vi kan beräkna F som $\displaystyle \frac{mv^2}{r}$ eftersom elektronerna rör sig i en cirkel.
Då får vi slutligen att $\displaystyle F_{medel} \approx 3.7 \cdot 10^{-16}N$ 

Detta svar stämmer enligt facit men jag tror inte att det var såhär det var tänkt att man skulle lösa uppgiften. Jag tycker min väg är rätt så komisk, men kanske inte det jag vill använda i framtiden! Hur ska man lösa det? Jag tänker att vi har ett medelvärde över ett kontinuerligt intervall och då borde man väl behöva beräkna en integral?