max och minipunkter
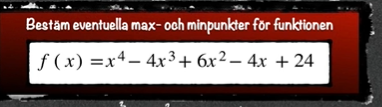
jag väljer att derivera först
f'(x) = 4x3 - 12x2 + 12x - 4
sedan vill jag få ut nollställen, men här får jag lite problem
4x3 - 12x2 + 12x - 4 = 0
4 (x3 - 3x2 + 3x -1) = 0
men kommer inte längre vid ekvationen
(tänker att när jag sedan får ut nollställena så kan jag göra en andraderivata och sätta in mina x-värden för att se om det är max/minpunkter?)
Ett knep för att gissa rötter till polynomekvationer:
Först ser man till att koefficienten för högsta gradtalet blir ett. Det har du redan fixat genom att bryta ut fyran. Du har ETT gånger x3.
Sedan tittar man på konstanttermen, den sista -1 i din parentes. Den faktoriserar man så mycket man kan. Just med ettan är det ju enkelt. Den blir helt enkelt 1. Om konstanttermen t.ex. hade varit 12 hade man faktoriserat till 2*2*3.
Sedan PROVAR man alla värden man kan hitta på från faktoriseringen, med olika tecken.
Du provar 1 och -1 som rötter.
Om konstanttermen hade varit 12 hade man behövt prova allt man kan multiplicera ihop: 1 och -1, 2 och -2, 3 och -3, 4 och -4, 6 och -6, 12 och -12.
Duger någon av 1 och -1 som rot?
Bubo skrev:Ett knep för att gissa rötter till polynomekvationer:
Först ser man till att koefficienten för högsta gradtalet blir ett. Det har du redan fixat genom att bryta ut fyran. Du har ETT gånger x3.
Sedan tittar man på konstanttermen, den sista -1 i din parentes. Den faktoriserar man så mycket man kan. Just med ettan är det ju enkelt. Den blir helt enkelt 1. Om konstanttermen t.ex. hade varit 12 hade man faktoriserat till 2*2*3.
Sedan PROVAR man alla värden man kan hitta på från faktoriseringen, med olika tecken.
Du provar 1 och -1 som rötter.
Om konstanttermen hade varit 12 hade man behövt prova allt man kan multiplicera ihop: 1 och -1, 2 och -2, 3 och -3, 4 och -4, 6 och -6, 12 och -12.
Duger någon av 1 och -1 som rot?
Tappar bort mig lite här..
ska jag alltså faktorisera konstanttermen och sedan använda mig utav de talen jag får för att sedan sätta in de istället för x? ...
((((( vi säger om jag hade haft talet 580 som konstantterm, hade inte det tagit lång tid att pröva sig fram med alla tal?
ur nyfikenhet måste jag fråga.. finns det en annan metod utöver denna där det itne är lika mycket pröva sig fram? )))))
... men eftersom vi hade -1 som konstantterm, ska jag då lägga in det istället för x:en?
då blir det
1 - 3 + 3 - 1
(uppskattar din hjälp)
Ja, knepet är att faktorisera konstanttermen.
I det här fallet är konstanttermen 1, så det räcker att testa 1 och -1
Om konstanttermen hade varit 580, så hade man först fått fram 580 = 1*5*2*2*29 och sedan behövt multiplicera ihop olika kombinationer av de faktorerna för att till slut prova allihop, med både positivt och negativt tecken.
Just tredjegradsekvationer KAN man lösa (redan på medeltiden i Italien!) , men det är riktigt jobbigt: https://sv.wikipedia.org/wiki/Tredjegradsekvation
Färdegradsekvationer är ännu värre, och för femtegradare och högre går det inte att hitta en analytisk lösning.
Bubo skrev:Ja, knepet är att faktorisera konstanttermen.
I det här fallet är konstanttermen 1, så det räcker att testa 1 och -1
Om konstanttermen hade varit 580, så hade man först fått fram 580 = 1*5*2*2*29 och sedan behövt multiplicera ihop olika kombinationer av de faktorerna för att till slut prova allihop, med både positivt och negativt tecken.
Just tredjegradsekvationer KAN man lösa (redan på medeltiden i Italien!) , men det är riktigt jobbigt: https://sv.wikipedia.org/wiki/Tredjegradsekvation
Färdegradsekvationer är ännu värre, och för femtegradare och högre går det inte att hitta en analytisk lösning.
intressant,
så nu har vi fått fram att x antingen är 1 eller -1, hur vet jag det? ska jag bara sätta in det i uttrycket och se till att det blir 0?
Ja,
Ett förtydligande: OM det är så att vår ekvation har rötter som är heltal, så finns de rötterna bland de tal som knepet ger oss.
Men vi vet ju inte alls om det är så. Det kan vara så att vi inte har några heltalsrötter.
I det här fallet är det i alla fall enkelt att prova. Blir parentesen noll om x=1? Blir parentesen noll om x=-1?
I fallet med 580 som konstantterm hade vi behövt prova 1, 2, 4, 5, 10, 20, 29, 58, 116, 145 och 290 (med plustecken och utan plustecken), totalt tjugotvå möjliga lösningar. Kanske hade inte någon av dem fungerat...
Bubo skrev:Ja,
Ett förtydligande: OM det är så att vår ekvation har rötter som är heltal, så finns de rötterna bland de tal som knepet ger oss.
Men vi vet ju inte alls om det är så. Det kan vara så att vi inte har några heltalsrötter.
I det här fallet är det i alla fall enkelt att prova. Blir parentesen noll om x=1? Blir parentesen noll om x=-1?
I fallet med 580 som konstantterm hade vi behövt prova 1, 2, 4, 5, 10, 20, 29, 58, 116, 145 och 290 (med plustecken och utan plustecken), totalt tjugotvå möjliga lösningar. Kanske hade inte någon av dem fungerat...
ja okej (:
jag testade sätta in både -1 och 1 och min "slutsats" är att 1 är det "korrekta"
ursäkta för frågorna, men hur tar jag reda på om det finns fler rötter?
Frågor är bra.
Du får dividera polynomet (x3 - 3x2 + 3x -1) med (x-roten), dvs med (x-1). Då får du kvar ett andragradspolynom, och det kan du hitta nollställen till.
naturnatur1 skrev:Bubo skrev:Ja,
Ett förtydligande: OM det är så att vår ekvation har rötter som är heltal, så finns de rötterna bland de tal som knepet ger oss.
Men vi vet ju inte alls om det är så. Det kan vara så att vi inte har några heltalsrötter.
I det här fallet är det i alla fall enkelt att prova. Blir parentesen noll om x=1? Blir parentesen noll om x=-1?
I fallet med 580 som konstantterm hade vi behövt prova 1, 2, 4, 5, 10, 20, 29, 58, 116, 145 och 290 (med plustecken och utan plustecken), totalt tjugotvå möjliga lösningar. Kanske hade inte någon av dem fungerat...
ja okej (:jag testade sätta in både -1 och 1 och min "slutsats" är att 1 är det "korrekta"
ursäkta för frågorna, men hur tar jag reda på om det finns fler rötter?
Satsen för detta kallas ibland för ”Satsen om heltalsrötter” och har ett ganska kort enkelt bevis om du är intresserad:

Bubo skrev:Frågor är bra.
Du får dividera polynomet (x3 - 3x2 + 3x -1) med (x-roten), dvs med (x-1). Då får du kvar ett andragradspolynom, och det kan du hitta nollställen till.
ska jag förenkla täljaren?
Tillägg: 3 apr 2023 23:49
x( x2 - 3x + 3 ) - 1 blir täljaren isåfall, vilket känns lite fel?
mrpotatohead skrev:
Satsen för detta kallas ibland för ”Satsen om heltalsrötter” och har ett ganska kort enkelt bevis om du är intresserad:
vad roligt, har inte sett det beviset innan. har du lust att visa exemplet också? (:
(det under (ex 9.7))
naturnatur1 skrev:Bubo skrev:Frågor är bra.
Du får dividera polynomet (x3 - 3x2 + 3x -1) med (x-roten), dvs med (x-1). Då får du kvar ett andragradspolynom, och det kan du hitta nollställen till.
ska jag förenkla täljaren?
Tillägg: 3 apr 2023 23:49
x( x2 - 3x + 3 ) - 1 blir täljaren isåfall, vilket känns lite fel?
Polynomdividera!

 Här är exempel med 4e-gradare😜
Här är exempel med 4e-gradare😜
mrpotatohead skrev:naturnatur1 skrev:Bubo skrev:Frågor är bra.
Du får dividera polynomet (x3 - 3x2 + 3x -1) med (x-roten), dvs med (x-1). Då får du kvar ett andragradspolynom, och det kan du hitta nollställen till.
ska jag förenkla täljaren?
Tillägg: 3 apr 2023 23:49
x( x2 - 3x + 3 ) - 1 blir täljaren isåfall, vilket känns lite fel?
Polynomdividera!
vet inte hur man gör, sökte och såg att det ingår i matte 4, så jag stöter nog på det snart efter denna kurs...
hittils har jag kommit fram till en rot (1), men kommer inte fram till fler (om det behövs?)
Polynomdivision är en utmärkt metod, men det finns även ett annat sätt som du kan använda med Matte 3-kunskaper.
Vi vet att x = 1 är ett nollställe till polynomet x3-3x2+3x-1, vilket betyder att (x-1) är en faktor I polynomet.
Det betyder i sin tur att polynomet kan skrivas (x-1)(ax2+bx+c), där a, b och c är konstanter.
Om vi nu multiplicerar ihop dessa faktorer och förenklar får vi ax3+(b-a)x2+(c-b)x-c.
Detta polynom ska alltså vara lika med x3-3x2+3x-1 för alla värden på x.
För att det ska vara möjligt så måste respektive koefficienter vara identiska, vilket ger oss ekvationssystemet
- a = 1
- b-a = -3
- c-b = 3
- c = 1
Lös det för att bestämma a, b och c.
Bubos tips om att faktorisera konstanttermen är utmärkt.
Innan man gör det så kan man pröva två supersnabba test för att avgöra om x = 1 eller x = -1 är ett nollställe.
=============
Test 1: Är x = 1 ett nollställe?
Om summan av polynomets koefficienter är lika med 0 så är svaret ja.
Exempel på polynom där x = 1 är ett nollställe:
- 5x3+11x2-3x-13, summan av koefficienterna är 5+11-3-13 = 0
- 7x2-x-6, summan av koefficienterna är 7-1-6 = 0
- -8x3+5x2+3, summan av koefficienterna är -8+5+3 = 0
========
Test 2: Är x = -1 ett nollställe?
Om summan av koefficienterna (med omvänt tecken på alla koefficienter som hör till udda exponenter) är lika med 0 så är svaret ja.
Exempel på polynom där x = -1 är ett nollställe:
- 2x3+3x2-1, "specialsumman" av koefficienterna är -2+3-1 = 0
- 3x3+7x2+6x+2, "specialsumman" av koefficienterna är -3+7-6+2 = 0
- x3+7x+8, "specialsumman" av koefficienterna är -1-7+8 = 0
============
Fördelen med metoden är att den snabbt kan svara på frågorna om x = 1 eller x = -1 är nollställen. Nackdelen är att den inte hittar andra nollställen.
Yngve skrev:Polynomdivision är en utmärkt metod, men det finns även ett annat sätt som du kan använda med Matte 3-kunskaper.
Vi vet att x = 1 är ett nollställe till polynomet x3-3x2+3x-1, vilket betyder att (x-1) är en faktor I polynomet.
Det betyder i sin tur att polynomet kan skrivas (x-1)(ax2+bx+c), där a, b och c är konstanter.
((((vi säger om nollstället istället hade varit 5
hade man fortfarande kunnat skriva (x-5) (ax2+bx+c) då eller är det annorlunda då?))))
Om vi nu multiplicerar ihop dessa faktorer och förenklar får vi ax3+(b-a)x2+(c-b)x-c.
Detta polynom ska alltså vara lika med x3-3x2+3x-1 för alla värden på x.
För att det ska vara möjligt så måste respektive koefficienter vara identiska, vilket ger oss ekvationssystemet
- a = 1
- b-a = -3
- c-b = 3
- c = 1
Lös det för att bestämma a, b och c.
a = 1 b = -2 c = 1
detta medför att vi får ekvationen
x2 - 2x + 1 = 0
löser man ut detta får man x= 1
så det visas sig alltså att denna ekvation endast har en rot? ( 1 )
andraderivatan blir: 12x2-24x+12
f''(1) = 0
naturnatur1 skrev:
((((vi säger om nollstället istället hade varit 5
hade man fortfarande kunnat skriva (x-5) (ax2+bx+c) då eller är det annorlunda då?))))
Ja, man hade fortfarande kunnat skriva (x-5)(ax2+bx+c).
a = 1 b = -2 c = 1
detta medför att vi får ekvationen
x2 - 2x + 1 = 0
löser man ut detta får man x= 1
så det visas sig alltså att denna ekvation endast har en rot? ( 1 )
Ja det stämmer. Den kallas då en trippelrot och innebär att polynomet kan skrivas (x-1)3. Det ger oss att förstaderivatan f'(x) = 4(x-1)3.
Kontrollera gärna att det stämmer genom att multiplicera ut kuben och jämför med ditt ursprungsuttryck för f'(x).
andraderivatan blir: 12x2-24x+12
f''(1) = 0
Ja det stämmer. Vet du vad det innebär avseende den stationära punkten vid x = 1?
Yngve skrev:naturnatur1 skrev:((((vi säger om nollstället istället hade varit 5
hade man fortfarande kunnat skriva (x-5) (ax2+bx+c) då eller är det annorlunda då?))))
Ja, man hade fortfarande kunnat skriva (x-5)(ax2+bx+c).
a = 1 b = -2 c = 1
detta medför att vi får ekvationen
x2 - 2x + 1 = 0
löser man ut detta får man x= 1
så det visas sig alltså att denna ekvation endast har en rot? ( 1 )
Ja det stämmer. Den kallas då en trippelrot och innebär att polynomet kan skrivas (x-1)3. Det ger oss att förstaderivatan f'(x) = 4(x-1)3.
Kontrollera gärna att det stämmer genom att multiplicera ut kuben och jämför med ditt ursprungsuttryck för f'(x).
ja, det stämmer jag fick att
4(x-1)3 = f'(x)
hur visste du att 4 var konstanten (kan man veta det utan att kolla på f'(x) "faktoriseringen"?)
andraderivatan blir: 12x2-24x+12
f''(1) = 0
Ja det stämmer. Vet du vad det innebär avseende den stationära punkten vid x = 1?
detta är antigen en min eller max punkt, jag väljer då därför ta reda på det genom förstaderivatan
f'(0) får jag till -4 och sätter jag in värden mindre och större än -4 i förstaderivatan får jag
- 0 +
vilket innebär att detta är en minimipunkt
och nu kan jag ta fram y-koordinaten genom att sätta in f(1) och därmed är uppgiften löst?
naturnatur1 skrev:
ja, det stämmer jag fick att
4(x-1)3 = f'(x)
hur visste du att 4 var konstanten (kan man veta det utan att kolla på f'(x) "faktoriseringen"?)
Du gjorde det jobbet själv, i första inlägget.
Du skrev där att f'(x) = 4x3-12x2+12x-4, vilket du faktoriserade till f(x) = 4•(x3-3x2+3x-1).
Uttrycket innanför parenteserna har vi faktoriserat till (x-1)3 och alltså är f'(x) = 4•(x-1)3
detta är antigen en min eller max punkt, jag väljer då därför ta reda på det genom förstaderivatan
f'(0) får jag till -4 och sätter jag in värden mindre och större än -4 i förstaderivatan får jag
- 0 + vilket innebär att detta är en minimipunkt
Du menar väl att du väljer x-värden mindre än och större än 1 (inte -4)?
Det du gör är en teckenstudie av förstaderivatan vid och runt den stationära punkten vid x = 1, vilket är en bra metod.
och nu kan jag ta fram y-koordinaten genom att sätta in f(1) och därmed är uppgiften löst?
Ja, extrempunktens y-värde fås av y = f(1).
Yngve skrev:naturnatur1 skrev:ja, det stämmer jag fick att
4(x-1)3 = f'(x)
hur visste du att 4 var konstanten (kan man veta det utan att kolla på f'(x) "faktoriseringen"?)
Du gjorde det jobbet själv, i första inlägget.
Du skrev där att f'(x) = 4x3-12x2+12x-4, vilket du faktoriserade till f(x) = 4•(x3-3x2+3x-1).
Uttrycket innanför parenteserna har vi faktoriserat till (x-1)3 och alltså är f'(x) = 4•(x-1)3
detta är antigen en min eller max punkt, jag väljer då därför ta reda på det genom förstaderivatan
f'(0) får jag till -4 och sätter jag in värden mindre och större än -4 i förstaderivatan får jag
- 0 + vilket innebär att detta är en minimipunkt
Du menar väl att du väljer x-värden mindre än och större än 1 (inte -4)?
Det du gör är en teckenstudie av förstaderivatan vid och runt den stationära punkten vid x = 1, vilket är en bra metod.
och nu kan jag ta fram y-koordinaten genom att sätta in f(1) och därmed är uppgiften löst?
Ja, extrempunktens y-värde fås av y = f(1).
skrev lite fel, menade givetvis 1,
tack så mycket för hjälpen!
har du någon liknande test uppgift som jag kan lösa för att kolla så att jag är med på banan? (:
hittar inte fler i boken:/
Pröva att faktorisera x3-7x-6
Yngve skrev:Pröva att faktorisera x3-7x-6
x (x2 - 7) - 6 ?
Nej, faktoriseringen ska bli på formen k(x-x1)(x-x2)(x-x3), där k är en konstant och x1, x2 och x3 är polynomets nollställen.
Använd tipsen och metoderna vi har visat i den här tråden.
Yngve skrev:Nej, faktoriseringen ska bli på formen k(x-x1)(x-x2)(x-x3), där k är en konstant och x1, x2 och x3 är polynomets nollställen.
Använd tipsen och metoderna vi har visat i den här tråden.
vi har uttrycket
x3 - 7x - 6
6an --> 2 * 3
testar jag sätta in 2 och 3 i uttrycket så ser vi att 3 är en rot.
så nu kan vi skriva (x-3) (ax2+bx+c)
och nu ska jag väl hitta värde på a , b och c?
c vet vi väl direkt att det är -6?
naturnatur1 skrev:
vi har uttrycket
x3 - 7x - 6
6an --> 2 * 3
testar jag sätta in 2 och 3 i uttrycket så ser vi att 3 är en rot.
så nu kan vi skriva (x-3) (ax2+bx+c)
Ja, det stämmer
och nu ska jag väl hitta värde på a , b och c?
c vet vi väl direkt att det är -6?
Pröva! Om c = -6, vad blir då konstanttermen?
Yngve skrev:naturnatur1 skrev:vi har uttrycket
x3 - 7x - 6
6an --> 2 * 3
testar jag sätta in 2 och 3 i uttrycket så ser vi att 3 är en rot.
så nu kan vi skriva (x-3) (ax2+bx+c)
Ja, det stämmer
och nu ska jag väl hitta värde på a , b och c?
c vet vi väl direkt att det är -6?
Pröva! Om c = -6, vad blir då konstanttermen?
när jag tog
(x-3) (ax2 + bx+c) fick jag det till
ax3 + (b-3a)x2 + (c-3b)x - 3c
vilket känns lite fel?
värdena blir isåfall
a= 1
b-3a= 0
c-3b = 7
c= 2
enligt b-3a= 0
så måste ju b vara 3
men om det sätts in här: c-3b = 7
så blir det ju inte rätt?
naturnatur1 skrev:när jag tog
(x-3) (ax2 + bx+c) fick jag det till
ax3 + (b-3a)x2 + (c-3b)x - 3c
vilket känns lite fel?
Nej, det stämmer.
värdena blir isåfall
a= 1
b-3a= 0
c-3b = 7
c= 2
enligt b-3a= 0
så måste ju b vara 3
men om det sätts in här: c-3b = 7
så blir det ju inte rätt?
Det stämmer att det inte blir rätt. Du har gjort fel på ett ställe. Försök att hitta det själv.
Yngve skrev:naturnatur1 skrev:när jag tog
(x-3) (ax2 + bx+c) fick jag det till
ax3 + (b-3a)x2 + (c-3b)x - 3c
vilket känns lite fel?
Nej, det stämmer.
värdena blir isåfall
a= 1
b-3a= 0
c-3b = 7
c= 2
enligt b-3a= 0
så måste ju b vara 3
men om det sätts in här: c-3b = 7
så blir det ju inte rätt?
Det stämmer att det inte blir rätt. Du har gjort fel på ett ställe. Försök att hitta det själv.
a = 1
då x3 (konstanten framför är 1)
sedan har vi b-3a vid x2 termen , men denna finns inte i ursprungsekvationen och därför bör
b-3a=0
dvs --------> b - 3 * 1 = 0
så b = 3
x-termen i ursprungsekv är -7
och i den "Nya" är den c-3b
dvs
c-3b = -7
och c i ursprungsekv är -6 och i den nya -3c (vilket medför att c = 2)
dvs c-3b = -7 blir
2 - 3b = -7
vilket gör att b även här blir
-3b= -9
b = 3
dvs
a= 1
b= 3
c= 2
vilket gör att den nya ekvationen ser ut såhär --> x2 +3x +2
dess rötter blir -1 och -2
dvs har vi rötterna
-1 , -2 och 3
så faktoriseringen blir
(x+1) (x+2) (x-3)
Ja, det stämmer.



