Max och min
Hej! har en fråga om uppgift 3b här nedan:
När jag studerar linjen som heter y=0 så får jag att :
f(x,y)=
fx är derivatan av f(x,y) mhp x. Jag har aldrig stött på att få en konstant när jag deriverar f(x,y) och således undrar jag vad det betyder? betyder det att punkten vi har en kritisk punkt vid (0,0) alltså att fx= konstant betyder att vi inte har något värde på x.

Hej.
På samma sätt som i det endimensionella fallet så betyder en konstant derivata att funktionsvärdet har konstant förändringstakt.
Om derivatan är lika med -4 så minskar funktionsvärdet med 4 för varje enhetsändring i positiv x-led.
Yngve skrev:Hej.
På samma sätt som i det endimensionella fallet så betyder en konstant derivata att funktionsvärdet har konstant förändringstakt.
Om derivatan är lika med -4 så minskar funktionsvärdet med 4 för varje enhetsändring i positiv x-led.
okej, jag förstår. Dock förstår jag inte vad facit försöker att säga här.
Insättningen av 3-x i f(x,y) ger en funktion vars derivata ( när derivatan lika med noll) ger kritiska punkter.
Men i fallet med y=0 har de inte deriverat funktionen som fås efter insättningen av y=0 i f(x,y).
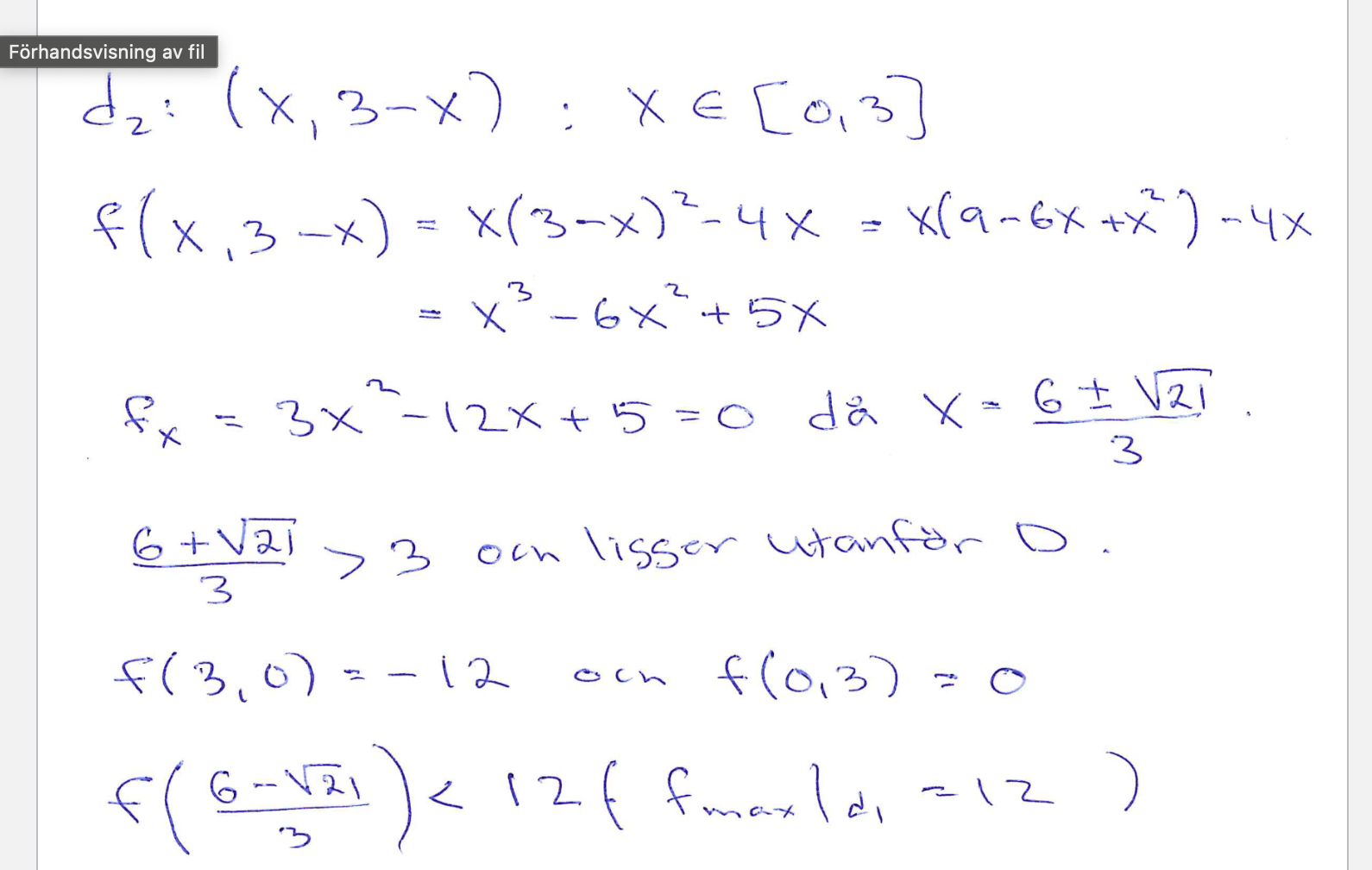

De tycker antagligen att -4x är en så enkel funktion att de kan avgöra minimum och maximum på linjestycket direkt.
Men formellt ska man derivera, konstatera att det inte finns någon extrempunkt och sedan kolla områdets hörnpunkter.



