Mattefysikprovet 2007 Q20

Triangeln du har ritat stämmer inte med beskrivningen.

Att höjden mot hypotenusan är 5 l.e. innebär dels att höjden är vinkelrät mot hypotenusan, dels att höjden är 5 l.e.

Jaha, det var nytt för mig. Tack!! Men, hur kommer man fram till att ingen sådan triangel finns?

Vi kallar sidorna i den stora triangeln för a och b, och vi kan dela upp hypotenusan i x och $8-x$. Vi vet att $a^2+b^2=8^2$, men från situationen: 

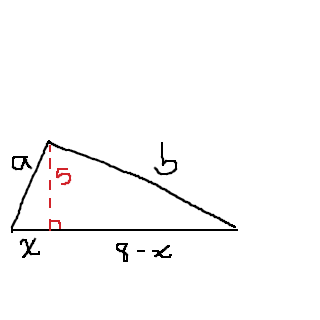
Vet vi också att $x^2+5^2=a^2$ samt att ${\left(8-x\right)}^2+5^2=b^2$. Kommer du vidare? :)

Ett inte helt strikt bevis men ändå:

- Är du med på att en rätvinklig triangels höjd mot hypotenusan är som störst då triangeln är likbent?
i så fall:

- En rätvinklig triangel som är likbent är ju oxå en halv kvadrat. Diagonalerna i en kvadrat är lika långa och därför blir höjden i en halv kvadrat lika med halva hypotenusan. (Rita upp det så ser du det direkt)

- För icke likbenta trianglar är höjden mot hypotenusan alltså < halva hypotenusan!

- I vårt fall är höjden 5 dvs ett omöjligt fall!

Säg att kateterna har längd a respektive b. Du har då:

$$\begin{gathered} a^2+b^2=64 \\ ab=40 \end{gathered}$$

Det ger dig:

${(a-b)}^2=a^2+b^2-2ab=-16$

vilket är omöjligt efter kvadraten av ett tal inte kan vara negativt.