Matte 5 skolverket kursprov vt14 uppgift differential ekvation utan räknare.
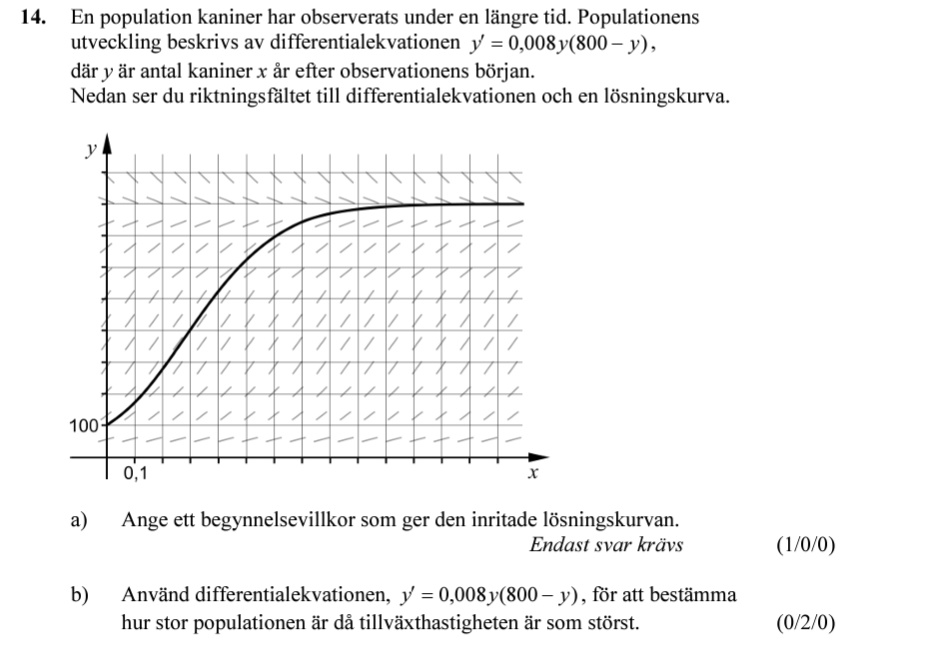
Uppgift b) har jag problem med, förstår inte hur jag ska lösa detta utan räknare, lyckades lösa det med räknare men utan vet jag typ inte ens hur jag ska börja, jag vet bara informationen som gavs av själva b) uppgiften samt begynnelse vilkoret y(0)=100. Något tips om hur jag skulle börja skulle uppskattas mycket :)
Nick12 skrev:
Uppgift b) har jag problem med, förstår inte hur jag ska lösa detta utan räknare, lyckades lösa det med räknare men utan vet jag typ inte ens hur jag ska börja, jag vet bara informationen som gavs av själva b) uppgiften samt begynnelse vilkoret y(0)=100. Något tips om hur jag skulle börja skulle uppskattas mycket :)
Derivatan är en andragradsfunktion. En andragradsfunktion har sitt största (eller minsta) värde på symmetrilinjen, d v s mittemellan nollställena.
Smaragdalena skrev:Nick12 skrev:
Uppgift b) har jag problem med, förstår inte hur jag ska lösa detta utan räknare, lyckades lösa det med räknare men utan vet jag typ inte ens hur jag ska börja, jag vet bara informationen som gavs av själva b) uppgiften samt begynnelse vilkoret y(0)=100. Något tips om hur jag skulle börja skulle uppskattas mycket :)
Derivatan är en andragradsfunktion. En andragradsfunktion har sitt största (eller minsta) värde på symmetrilinjen, d v s mittemellan nollställena.
Förstår inte riktigt hur detta hjälper mig
Förstår inte riktigt hur detta hjälper mig
Är du med på att "då tillväxthastigheten är som störst" betyder "när derivatan är som störst"?
Smaragdalena skrev:Förstår inte riktigt hur detta hjälper mig
Är du med på att "då tillväxthastigheten är som störst" betyder "när derivatan är som störst"?
Ja men vet inte vad jag kan göra det det
Ta reda på var derivatan är som störst - du behöver inte ens derivera för att göra det!
Smaragdalena skrev:Ta reda på var derivatan är som störst - du behöver inte ens derivera för att göra det!
Jag vet inte hur, jag kanske bara är trög.
Kolla där lutningen är störst (lutar brant upp).
Du har diffekvationen y' = ay(b-y) = aby-ay2, d v s derivatan är en andragradsfunktion. Om du tittar på funktionen ser du att den har negativ koefficient för andragradstermen, d v s derivatan ser ut så här: . "Toppen" är på symmetrilinjen, som ligger mittemellan nollställena, och nollställena har du gratis, om du inte multiplicerar ihop derivatan. Vilket tal ligger mittemellan 0 och 800?
Smaragdalena skrev:Du har diffekvationen y' = ay(b-y) = aby-ay2, d v s derivatan är en andragradsfunktion. Om du tittar på funktionen ser du att den har negativ koefficient för andragradstermen, d v s derivatan ser ut så här: . "Toppen" är på symmetrilinjen, som ligger mittemellan nollställena, och nollställena har du gratis, om du inte multiplicerar ihop derivatan. Vilket tal ligger mittemellan 0 och 800?
Okej men vart får vi 0 och 800? jag ser inte riktigt det i funktionen, men det blir 400 skulle jag vilja tro.
Ett av derivatans nollställen ligger vid och det andra ligger vid .
naytte skrev:Ett av derivatans nollställen ligger vid och det andra ligger vid .
varför då
Testa att beräkna y'(800 kaniner) och y'(0 kaniner) så ser du att båda blir noll.
naytte skrev:Testa att beräkna y'(800 kaniner) och y'(0 kaniner) så ser du att båda blir noll.
Så jag sätter in 800 och 0 som mitt y i 2 separata tillfällen och får det till 0 därför är de mina nollställen?
Ja, det är det som nollställen betyder: de värden på det man stoppar in (i detta fall y) som gör att funktionen (i detta fall y') blir noll. Och en andragradskurva har bara två nollställen. Mitt emellan dessa ligger symmetrilinjen och där finns maximi- eller minimivärdet.





