Matte 5- omfångsrika problem

Det enda jag har kvar är hur långa ben som scenen kommer få, jag tänker att volymen av byggnaden kommer se ut som en tratt, därför kommer scenen behöva längre ben där bak än där fram. Och benens längd borde vara som en funktion av resten av tratten, men vet inte riktigt hur jag ska gå vidare

Jag förstår inte alls vad du menar. Kan du rita en figur? Enligt min uppfattning behöver du inte ha någon lutning alls vid scenen. Sedan undrar jag; får du välja allting helt och hållet själv eller vad är egentligen problembeskrivningen? Är den bara:

"Designa en aula med hjälp av Geogebra."

Känns lite enkelt.

Tillägg: 10 maj 2022 14:58

Jaha, nu förstår jag. Om du menar vad jag tror skulle jag inte rekommendera den designen. Försök, om du kan, rita en figur så att jag får se mer tydligt hur du tänkt att det kommer se ut.

Figuren som jag visade där uppe visar hur byggnaden ska se ut, min lärare vill alltså att den ska se ut så. I första bilden kan man tänka sig att scenen är vid origo ungefär, när figuren roterar kring y-axeln kommer scenen att bildas tillsammans med aulan och hallen. 

Är det godtyckligt upp till dig vad dimensionerna på scenen ska vara?

Det framgår inte några dimensioner i några av bilderna. Använd hursomhelst diagonalen till hörnet i punkten (x,y) du vill veta höjden relativt marken hos. Alltså:

$d = \sqrt{x^2+y^2}$

För detta hörn är avståndet du då beräknar samma sak som horisontella avståndet längs med marken. Då får du höjden som:

$h = d \cdot \tan(\alpha)$

Här vet vi att lutningen $k$ på "läktaren" där människor sitter ges av:

$k = \tan(\alpha)$

Det är precis så jag tänkte också, jag har själv bestämt scenens mått till 10x6 och sedan 2,5 meters höjd. Det fick vi bestämma, och k har jag bestämt till 0,3. Och då tänkte jag att de främre benen av scenen har höjden 2.5- ( 0,3x7,8). 7,8 då det är hypotenusan av scenen. Men min lärare säger att det nämligen är mer besvärligt än såhär, han föreslog att jag skulle skära ett papper i rektangulär form och sedan lägga i en tratt hemma för att kunna visualisera. Men jag förstår frf inte, hur kan benens höjd vara i funktion till resten av ”tratten”?

Är detta vad du menar:

Scenen i rött sett från sidan och uppifrån. Kan du dela .ggb-filen?

Tillägg: 10 maj 2022 22:52

Du kan få tag i den filen genom att öppna vänstra menyn på hemsidan och trycka på "Ladda ned som" eller exportera om du har programmet på datorn.

Ebola skrev:

Är detta vad du menar:

Scenen i rött sett från sidan och uppifrån. Kan du dela .ggb-filen?

---

Tillägg: 10 maj 2022 22:52

Du kan få tag i den filen genom att öppna vänstra menyn på hemsidan och trycka på "Ladda ned som" eller exportera om du har programmet på datorn.

Scenen måste väl  ligga så att det är positiva y-koordinater, inte negativa? Annars verkar det som en konstig aula.

Ja det är precis så jag menar, varför skulle det inte kunna hamna på negativa x-kordinater, det här är ju bara för att föreställa oss hur det ska se ut.

Sorry jag misstolkade det du skrev, ja det är egentligen positiva y-kordinater, jag tror att jag råkade vrida fel på geogebra. 

den här bilden gör det kanske tydligare

Så du menar att bilden jag skickade är rätt? Alltså att scenen ska vara i mitten? Eller ska den vara ovanför?

ja den är rätt. Den ska vara i mitten

Okej. Du är alltså säker på att det inte ska vara som i GIF-bilden nedan där scenen är "utanför" rotationskroppen:

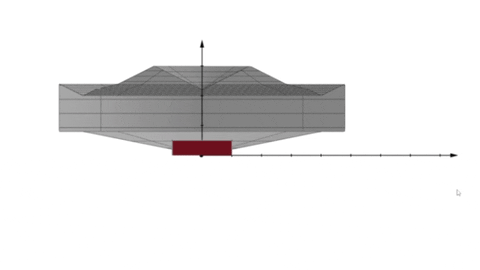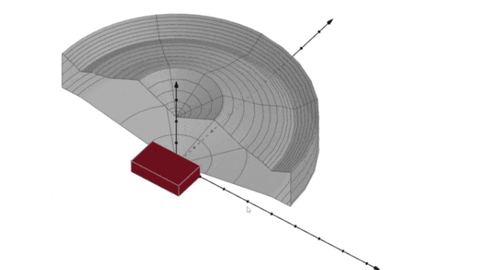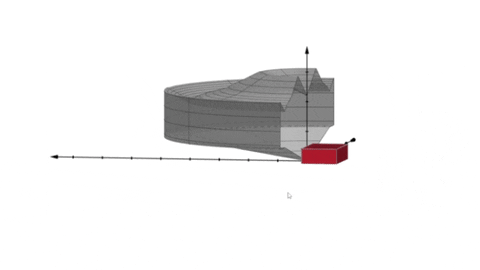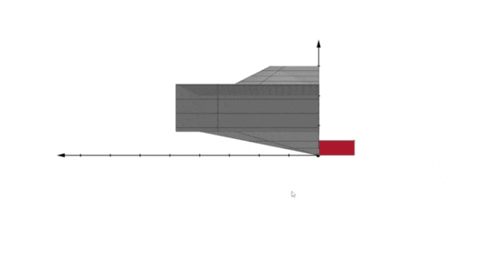
För om den ska vara "inuti" volymen förstår jag ärligt talat inte vad din lärare vill utan tycker att du löst den. Någon annan kanske förhoppningsvis förstår.

Det är just det, den är inuti volymen, inte utanför. Det enda han gav mig för ledtråd var att det handlar om en tratt och att benens höjd borde vara en funktion av resten. Jag uppskattar ändå dina försök

Okej. Men titta på nedan bild:

Om den är inuti, 10x6x2.5 kommer höjden på "benen" ges av lutningen och diagonalen från origo till hörnet. Det ser man väldigt tydligt i bilden ovan... Jag kan till och med modellera det i geogebra matematiskt så att det fungerar :D

Det enda jag kan tänka mig är att höjden på scenen kommer variera. Alltså att det inte ska vara ben utan ett rätblock med variabel höjd längs med aulans golv. Då blir det lite svårare och man måste tänka lite.

Tillägg: 11 maj 2022 13:08

Om jag förstår din lärare rätt så är det så här den menar:

Alltså att höjden på scenen följer en funktion. Här ser vi till exempel rakt framifrån scenen och dess höjd där ser ut att följa en andragradsfunktion. Jag tycker man kan se samma sak från sidan:

Ahaaa, men det blir alltså inte ett rätblock. Och det är så på grund av "tratten"

Hej Ebola, jag pratade med min lärare och tydligen hade vi rätt i början när vi tänkte att man ska använda diagonalen till hörnet i punkten (x,y). Jag tror att han missförstod vad jag menade. Jag ber hursomhelst om ursäkt för besväret och uppskattar verkligen hjälpen, TACK!

Hej, jag undrar bara, är detta en del av matte 5?? Har slutprov om några dagar o aldrig gjort något liknande!!

Nej det är inte alla skolor som har såhär tror jag. Du behöver inte oroa dig

Okej, vad skönt! Att göra det i Geogebra är ganska lätt med lite pill men att beskriva det matematiskt kräver nog egentligen universitetsnivå. Det som sker är att du kan beskriva höjden i z-led som nedan (denna definition är alltså om polygonen är i x-y-planet och man roterat runt z-led):

$z = \sqrt{x^2+y^2}\cdot k$

Nu beror det då på vilken av scenens sidor du tittar på. Du får olika kurvor för olika sidor. Här får du i alla fall se hur scenen ser ut med den tolkningen du gjorde:

Det som är svårt är att beskriva ytan på undersidan som kräver något som kallas "parametrisering". Detta kommer du lära dig mer om ifall du läser linjär algebra och flervariabelanalys. Här syns resultatet i rörlig form:

En fråga, hur kan jag göra som du gjorde och sätta in det i min geogebra. Det är väl geogebra du använder? Och sedan vill man ju ha en scen som är rak, blir det då att man fyller i det tomma med betong eller? Jag är inte säker på om jag förstår den första bilden du konstruera heller 

fysikopium skrev:

En fråga, hur kan jag göra som du gjorde och sätta in det i min geogebra. Det är väl geogebra du använder?

Jag kan dela min .ggb-fil, hämta den här:

https://filetransfer.io/data-package/VlXgr91g#link

Det blir som vanligt lite laggigt i Geogebra men det går, annars får du säga till. Vinkeln "v1" som är längst upp avgör vinkeln från 0 till 180 grader på rotationen för rotationsvolymen.

Och sedan vill man ju ha en scen som är rak, blir det då att man fyller i det tomma med betong eller? Jag är inte säker på om jag förstår den första bilden du konstruera heller 

Scenen är rak (eller plant horisontell) på ovansidan men kurvad på "undersidan". Den är helt enkelt anpassad efter att aulan lutar. Men, det har inte så mycket med verkligheten att göra, tror jag. Jag tror inte att det skulle finnas någon som helst fördel med att konstruera så här mer än att kanske få publiken att känna sig närmre dem på scen. Jag kan ha fel.

Tillägg: 11 maj 2022 16:40

Du måste förövrigt öppna filen i 3D-geogebra:

https://www.geogebra.org/3d?lang=sv

eller i dator-programmet Geogebra classic 6:

https://www.geogebra.org/download

Det blir fel när jag ska öppna, kan du visa mig det som står till vänster så jag kan skriva in det själv.

Det va inget, jag lyckades 

en fråga, varför definierade du denna på detta vis?

fysikopium skrev:

en fråga, varför definierade du denna på detta vis?

 

 

Höjden $z =p(x,y)$ till någonstans på den sidan där $y=6$ ges av den relationen enligt pythagoras sats. Du har först och främst avståndet från origo till någon punkt i x-y-planet som:

$d = \sqrt{x^2+y^2}$

Sedan vet vi att lutningen $k$ på Aulan ger oss höjden vid den punkten $z(x,y)$ från trigonometri som:

$z = d \cdot k$

Detta beskrev jag i inlägget här:

Länk till inlägg

Jag har satt $k=1/5$ vilket är varför den faktorn är där. Sedan har vi att för kortsidorna på scenen har vi $x=\pm 5$ vilket ger:

$z=\sqrt{5^2+y^2}\cdot \dfrac{1}{5}$

Sedan har vi för framsidan av scenen där $y=6$ att:

$z = \sqrt{x^2+6^2}\cdot \dfrac{1}{5}$

Tillägg: 11 maj 2022 20:00

Sedan ser jag nu efter många om och men att botten inte är helt korrekt definierad men att göra en sådan parametrisering är väldigt krånglig. 

Va menar du med att botten inte är helt korrekt definierad,

Jag har försökt nu återskapa scenen på egen hand, med hjälp av polynom då. Men hur skapar jag en yta som du har gjort

Va menar du med att botten inte är helt korrekt definierad,

Om du kollar på kortsidorna ser du att bottens kant inte är riktigt samma som kortsidan. Bottens kant är en tredjegradare eller något men sidans kant är en andragradare.

Men hur skapar jag en yta som du har gjort

För att skapa ytor på det här viset måste du parametrisera kurvorna som beskriver alla sidor på scenen. Det är överkurs men här kan du läsa om det:

https://wiki.geogebra.org/en/Curves 

Exempelsida:

https://www.geogebra.org/m/cAsHbXEU

Parametrisk yta:

https://wiki.geogebra.org/en/Surface_Command

https://www.geogebra.org/m/BjV7cNwb

Parametrisk yta mellan kurvor:

https://www.geogebra.org/m/tQ9DWUUS