Matte 5

Det finns inget NP för matte 5, och det frivilliga kursprov som finns har inget övningsprov. Det är därför svårt att säga vad som är viktigast, men enligt matteboken.se ingår följande områden:

• Mängdlära
• Kongruensräkning
• Talföljder och induktionsbevis
• Kombinatorik
• Grafteori
• Differentialekvationer

Med det sagt: dags att starta Matte 5 Bootcamp 2018!

Mängdlära: 

Relevanta begrepp:

1. Mängd: En samling av någonting, inom matematiken oftast siffror och tal. Innehållet i en mängd skrivs inom hakparenteser: Mängden av innehållet i en fruktsallad kan vara ${\mathrm{M}}_{\mathrm{fruktsallad}}=\left\{\mathrm{Kiwi}, \mathrm{apelsin}, \mathrm{vindruva}, \mathrm{banan}, \mathrm{carambola}, \mathrm{physalis}\right\}$. Mängden åldrar i en klass kanske är ${\mathrm{M}}_{\mathrm{förskoleklass}}=\left\{6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 38\right\}$. 
2. Element: En term i en mängd, exempelvis Kiwi i fruktsalladsmängden ovan.
3. Tomma mängden: Mängden som inte innehåller någonting. Den brukar skrivas $\left\{\varnothing \right\}$.
4. Union: Om du har två mängder, A och B, är unionen alla element som ingår i antingen A eller B, eller båda. Union betecknas $\cup$.
5. Snitt: Om du har två mängder, A och B, är snittet mellan dem alla element som ingår i både A och B. Snitt betecknas $\cap$.
6. $A\backslash B$: Betyder "i A, men inte i B". Alla element som ingår i A, förutom de element som ingår i både A och B.
7. Venndiagram: Diagram som visar hur två mängder förhåller sig till varandra.
   
8. Disjunkta mängder: Två mängder som inte har något gemensamt. Snittet av dessa mängder är den tomma mängden.
9. Universella mängden: Allt som ingår i undersökningen. Om du undersökt vilka husdjur en grupp har, är den universella mängden alla som har katt, alla som har hund, alla som har kanin, alla som har råtta, någon blandning, och alla som inte har djur. Denna mängd brukar betecknas U. 

Typiska uppgifter:

• 200 personer frågas om vilka djur de gillar. 110 pers. svarade hund, 70 personer svarade katt, och 50 personer svarade att de hatar djur och all glädje i hela universum. Hur många personer gillar bara katter? (Förutom Daja). Hur många personer gillar både katter och hundar?
• 70 personer ska träffas för att åka på en resa. 40 personer har packat skidor, 35 personer har packat varm choklad. 30 personer har packat både skidor och choklad. Hur många personer har inte packat någonting?

Kongruensräkning: Detta kapitel handlar om vad som blir över vid uppdelning i olika grupper, helt enkelt.

Om vi vill dividera femton med sex, kan vi skriva kvoten som 2,5. Vi kan också skriva att 15/6 = 2 rest tre, alternativt 15 = 6*2 + 3. 

Moduloräkning utgår ifrån vad resten blir när vi dividerar med olika tal. Ett trestreckigt likamed-tecken, $\equiv$, används för att beteckna detta, samt en (mod x) efteråt. I exemplet ovan blir det $15\equiv 3 (\mathrm{mod} 6)$. Dvs. Om vi räknar med 6-hopp på tallinjen blir resten av talet 15 lika med tre. Om talen a och b får samma rest vid division med ett visst tal, säger vi att de är "kongruenta modulo n". 

Räkneregler (med exempel): 

• $$\begin{gathered} a+b (mod n) = a (mod n) + b(mod n) \\ 13+17 (mod 4)=13 (mod 4) + 17 (mod 4)=1+1=2 \\ 13+17 (mod 4)=2 \end{gathered}$$
• $$\begin{gathered} a·b (mod n)=a (mod n) · b (mod n) \\ 13·17 (mod 4)=13 (mod 4) · 17 (mod 4)=1·1=1 \end{gathered}$$
  
  
• $$\begin{gathered} a^m (mod n) = (a (mod n){)}^m \\ {10}^3 (mod 8) = (10 (mod 8){)}^3=2^3= 8 (mod 8) =0 \\ (\frac{1000}{8} \mathrm{går} \mathrm{alltså} \mathrm{jämnt} \mathrm{ut}) \end{gathered}$$

Det är främst den tredje regeln som är riktigt användbar. Typiska uppgifter är sådant som: 

1. Klockan är 15:00. Vad är klockan om 2^28 sekunder? 
2. Vilken är den sista siffran i 92^8?
3. Idag är det tisdag. Vilken veckodag är det om en miljard dagar?

Talföljder och induktionsbevis:

Begrepp: 

1. Aritmetisk talföljd: En talföljd där skillnaden mellan två element i rad är samma, exempelvis 1, 3, 5, 7, 9. (tidigare element +2)
2. Geometrisk talföljd: En talföljd där förhållandet mellan två element i rad är samma, exempelvis 1, 3, 9, 27, 81. (tidigare element *3)
3. Sluten formel: En formel där vi direkt kan beräkna värdet på det n:te elementet i talföljden. 
4. Rekursiv formel: Motsatsen till en sluten formel, vi måste veta värdet på elementet innan för att kunna räkna ut nästa element. Det mest klassiska exemplet är Fibonaccis talföljd: 1, 1, 2, 3, 5, 8, 13... För att ta reda på det 25:te elementet MÅSTE vi räkna oss fram. Vi kan inte addera element nummer ett till 25*differensen, som vid en aritmetisk talföljd. 

Och nu till det som faktiskt är viktigt med detta kapitel: induktionsbevis! Detta är en oerhört listig bevismetod, som görs i tre steg.

Steg ett: visa att påståendet är sant för ett basfall.
Steg två: anta att påståendet är sant för n = k. 
Steg tre: visa att om påståendet är sant för n = k, är påståendet sant för n = k + 1. 

Det innebär att vi har bevisat att ett påstående är sant för n = k + 1, om det är sant för n = k. Men tidigare bevisade vi ju att det var sant för n = 0 eller 1, eller ett annat basfall. Då måste det vara sant för n = 1 + 1 = 2. Eftersom det är sant för n = 2, måste det vara sant för n = 2 + 1 = 3, osv. Vi puttar ned en dominobricka, och då faller nästa, som fäller nästa, som fäller nästa. Sedan filmar vi skiten, och lägger ut på Youtube och får en massa annonsintäkter. 

Exempel: Bevisa att $\sum _{i=0}^n{2}^i=2^{n+1}-1$.

1. Basfall: n = 0. 

$$\begin{gathered} 2^0=2^{0+1}-1 \\ 1=2^1-1 \\ 1=2-1 \\ 1=1 \\ VL=HL \end{gathered}$$

Alltså är påståendet sant då n = 0.

2. Antagande: Vi utgår ifrån att påståendet är sant om n = k. Detta ger oss att $\sum _{i=0}^k{2}^k=2^{k+1}-1$.

3. Watch the magic now:

Vi sätter att n = k + 1:

$$\begin{gathered} \sum _{i=0}^{k+1}{2}^k=2^{(k+1)+1}-1 \\ \sum _{i=0}^{k+1}{2}^k=2^{k+2}-1 \\ \sum _{i=0}^{k+1}{2}^k=\sum _{i=0}^k{2}^k+2^{k+1} \\ \sum _{i=0}^k{2}^k+2^{k+1}=2^{k+2}-1 \end{gathered}$$

Men, vi vet ju att den vänstra termen i VL (med summaformeln) är lika med 2^(k+1)-1, enligt vårt antagande. Då kan addera det uttrycket till VL, och vi får:

$$\begin{gathered} (2^{k+1}-1)+2^{k+1}=(2^{k+2}-1) \\ {2}^{k+1}+2^{k+1}-1=2^{k+2}-1 \\ 2·2^{k+1}-1=2^{k+2}-1 \\ {2}^{k+2}-1=2^{k+2}-1 \\ Q.E.D. \end{gathered}$$

Exempeluppgifter är att bevisa följande:

• $\sum _{i=1}^n(2k-1)=n^2$
• $2^n>n^3, n\ge 10$
• $\sum _{i=1}^n\frac{1}{\sqrt{i}}<2\sqrt{n}-1$

Kombinatorik: 

Två väldigt viktiga begrepp:

Permutation: Ett alternativ där ordningen spelar roll. 123 är inte samma sak som 321.

Kombination: Ett alternativ där ordningen inte spelar roll: 123 är samma sak som 321. 

Formeln som används för att beräkna antalet permutationer är $\frac{n!}{(n-r)!}$, där n är det totala antalet element, och r det antal element som väljs. Om du ska välja rektor, ordförande och sekreterare bland sju personer (ordningen spelar roll) är det totala antalet element 7 st, och antalet element som väljs 3 st. Formeln blir då 7!/4!. Det är egentligen samma sak som 7*6*5, bara att det är ett smidigare sätt att skriva på.

Formeln som används för att beräkna antalet kombinationer på är $\frac{n!}{r!(n-r)!}$. n och r är samma som ovan. Detta skrivs ofta som $\left(\begin{array}{c}n\\ r\end{array}\right)$. En räkneregel som gäller är att $\left(\begin{array}{c}n\\ r\end{array}\right)=\left(\begin{array}{c}n\\ n-r\end{array}\right)$. 

Uppgifter:

• På hur många sätt kan fem hockeyspelare väljas utav de 13 i laget, om alla har olika positioner på isen? 
• På hur många sätt kan samma hockeyspelare väljas i fråga om vilka som står på prispallen?
• Bevisa den kombinatoriska räkneregeln ovan.
• Fyra flickor och fyra pojkar ska väljas till elevrådet. Det finns 60 elever, 50/50 flickor och pojkar. På hur många sätt kan elevrådet väljas? (Alla har samma platser)
• Klantssons målerifirma målar staket. Du kan välja på blått, rosa, gult, rött, och grönt. På hur många sätt kan staketet målas? (Mycket svår uppgift)

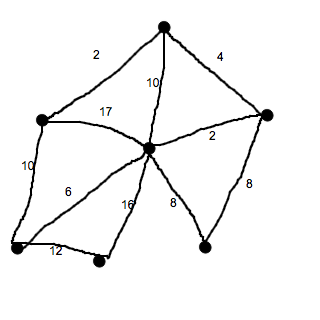
Grafteori: 

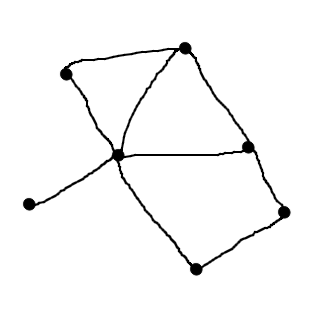
En graf är en bild över en koppling mellan ett antal olika punkter. Exempelvis:

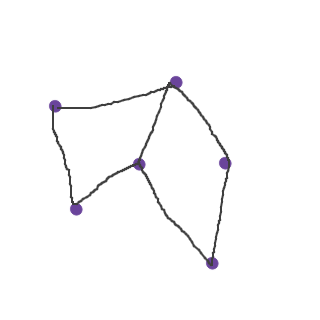
Punkterna (lila) kallas noder, och strecken (gråsvarta) kallas kanter. Grafteori handlar om hur dessa punkter är sammankopplade. Det finns framförallt två olika typer av kopplingar:

1. Euler-: alla kanter ska gås, men varje punkt får besökas flera gånger.
2. Hamilton-: varje kant måste inte gås, men varje punkt måste besökas precis en gång.

Dessa två kopplingar finns sedan i två varianter:

a) väg - varje nod/kant besöks en gång, men vandringen börjar inte på samma ställe som den slutar.
b) cykel - varje kant/nod besöks en gång, och när vi är runt kan vi fortsätta gå samma väg om och om igen, utan att behöva lyfta pennan från pappret.

Antalet kopplingar till varje nod kallas valens.

För Eulervägar och -cykler finns varsin regel:

1. En Eulerväg finns om max två noder har udda valens.
2. En Eulercykel finns om alla noder har en jämn valens.

För Hamiltonvägar finns inte samma typer av regler. Det gäller att en får prova sig fram. En metod som dock används ibland är närmaste granne-metoden. Denna metod ger ofta en bra lösning, men inte alltid den bästa. Börja i en given nod, och gå den kortaste sträckan till nästa nod. Gå nu den kortaste sträckan till en annan nod. Fortsätt så, utan att gå samma kant två gånger. Då fås en Hamiltonväg som är kort, men inte nödvändigtvis kortast. För att hitta den kortaste vägen måste alla stigar räknas ut och jämföras.

Uppspännande träd: Ett annat grafteoretiskt problem handlar om att hitta en koppling mellan alla ingående noder, utan upprepning. Detta kallas för ett uppspännande träd. Till skillnad från vägarna måste det inte vara möjligt att gå sträckan. Ett uppspännande träd kan se ut som nedan:

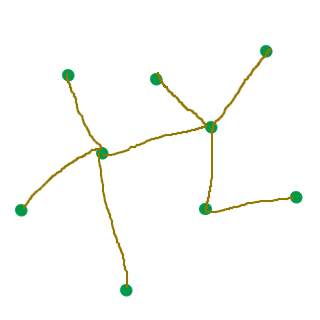
Om varje sträcka har en vikt, exempelvis kostnaden för att dra en fiberkabel mellan de olika punkterna, kan det billigaste trädet hittas. Detta kallas minimalt uppspännande träd, och kan hittas med Kruskals algoritm. Börja med den billigaste sträckan. Välj sedan den näst billigaste sträckan, och fortsätt så. De utvalda sträckorna behöver inte sitta ihop från början. Det viktiga är att det i slutändan blir ett träd utan cykler. 

Exempel:

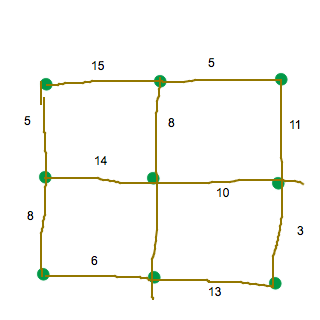
Nio hus ska kopplas samman med en fiberkabel. Hur ser den billigaste layouten ut? Vi börjar med den billigaste sträckan:

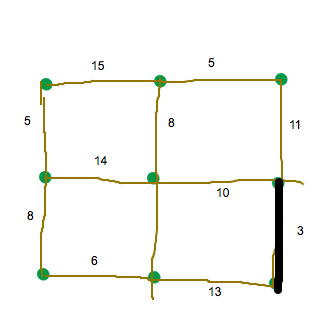
Sedan fortsätter vi med att hitta de billigaste sträckorna:

Allt som allt får vi trädet:

Exempeluppgifter:

Går det att hitta en Eulerväg i figurerna nedan? Går det att hitta en Hamiltonväg? Går det att hitta några cykler? Varför/varför inte?

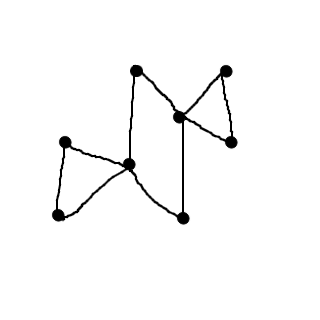
Hitta figurens minimalt uppspännande träd. Hur mycket kostar det?

Differentialekvationer: 

• Diffar med villkor: 
  
  $$\begin{gathered} y\text{'}+5y=0 \\ y\text{'}\left(0\right)=4 \\ y\left(0\right)=3 \end{gathered}$$
  
  Använd standardlösningen för diffar av första graden, och sätt in villkoren för att få ut en exakt lösning.
• Inhomogena diffar: Ett exempel är $y\text{'}+5y=x+4$
  
  Dela upp diffen i en allmän lösning (H) och en partikulärlösning (P). Det gäller att $y=y_H+y_P$. Den allmänna lösningen är lösningen till $y\text{'}+5y=0$, och partikulärlösningen ser till att vi får rätt högerled. 
  
  Den allmänna lösningen löses som vanligt. Partikulärlösningen fås genom att anta att lösningen finns på samma form som högerledets funktion. I detta fall är partikulärlösningen skriven på formen f(x) = ax + b. Ansättningen deriveras, f'(x) = a. Detta sätts in i VL:
  
  a + 5(ax + b) = x + 4
  a + 5ax + 5b = x + 4.
  
  Matcha termer av samma grad, vilket ger ekvationssystemet:
  
  $\left\{\begin{array}{l}a+5b=4\\ 5ax=x\Rightarrow 5a=1\end{array}\right.$
  
  Lösning av detta system ger partikulärlösningen y = 0,2x + 0,76. 
  
  Beroende på vilken funktion HL är, används olika ansättningar:
  1. En konstant => y = k
  2. En förstagradsfunktion => y = ax + b
  3. Polynomfunktioner generellt: => y = allmän form av polynomfunktion med samma grad
  4. Trigonometrisk funktion => y = acoskx + bsinkx (k har samma värde som ursprungsfunktionen)

Typiska uppgifter:

• y''+ y' +5y = 2x + 7
• y' + 2y = x^2+3x-4
• y'-3y = cos2x

Partiell integration (bonus): Detta finns inte med i det centrala innehållet i kursen, men vi gick igenom det och det är faktiskt användbart vid problemlösning, men vi går igenom det snabbt, eftersom det inte är så viktigt.

$\int f\left(x\right)·g\left(x\right)dx=F\left(x\right)·g\left(x\right)-\int F\left(x\right)·g\text{'}\left(x\right)dx$

Genom att välja f(x) och g(x) rätt kan en spara väldigt mycket tid vid integreringar.

Exempeluppgifter:

• $\int (2x·\sin x)dx$
• $\int (x^2·\ln x)dx$

Detta är teorin i matte 5. Gör många uppgifter i boken, och det kommer att gå bra.

Omg... wow. Your kungfu is strong.

Innan jag börjar bearbeta detta, måste jag ta några kaffer. Kanske även direkt i blodströmet.

... och jag måste nog uppdatera GöteborgsPostens artikel.

Hehehehehe :)

Nämen detta var faktiskt otroligt, och mycket bra skriven dessutom! Jag MÅSTE läsa om det imorgon bitti (pga bland annat förfarligt ljudnivå i huset just nu) och testa mig på dina uppgifter. Jag har totalt missat delen där the magic happens.

Jag fattar inte ens hur du kan komma ihåg det?

Tror du att det fortfarande går att sälja själen till Satan? Jag är alltid så ful på bilderna!

Edit: några spännande reklam-fyllde youtube klipper att rekommandera för induktionsbevis? (det ser ut som det svåraste) (... det kanske beror på att jag var inte rikigt med kombinatorism)

Tackar tackar! 

Jag har en magisk hjärna som är direkt uppkopplad mot google. Glömmer jag något märks det inte. :)

Jag har försökt. Satan svarade att han inte var intresserad. Det är illa, va?

Nja, egentligen inte. När det kommer till induktionsbevis är det mycket en fråga om att försöka göra själv. Varje bevis har sin egen bevisprocess. Jag föreslår att du väljer några olika påståenden, ta de jag skrev för enkelhetens skull, och sedan skriver du upp ditt försök i en tråd, så tar vi det därifrån. Du kommer att utvecklas mycket mer på att utföra induktionsbevis själv.

Otroligt snyggt Smutstvätt! Tvätten är skinande ren 2018!

dajamanté, förslår att du börjar med att bevisa den klassiska Gauss-formeln med induktionsbevis:

$1+2+3+...+(n-1)+n = \frac{n(n+1)}{2}$

Smutstvätt skrev :

---

Typiska uppgifter:

• 200 personer frågas om vilka djur de gillar. 110 pers. svarade hund, 70 personer svarade katt, och 50 personer svarade att de hatar djur och all glädje i hela universum. Hur många personer gillar bara katter? (Förutom Daja). Hur många personer gillar både katter och hundar?
• 70 personer ska träffas för att åka på en resa. 40 personer har packat skidor, 35 personer har packat varm choklad. 30 personer har packat både skidor och choklad. Hur många personer har inte packat någonting?

• Den blir nog 39 va, efter jag tog bort migsjälv?

Brrr, bara att rita det tog tillbaka gamla mardrömmar om eukaryota celler.

• det blir 35 skitstövlar?

Klockan är 15:00. Vad är klockan om 2^28 sekunder?
Vilken är den sista siffran i 92^8?
Idag är det tisdag. Vilken veckodag är det om en miljard dagar?

1. Fyf... alltså. Den här är jag fortfarande inte med.

Men ok då, om vi säger att $2^{6}$ ger 64, som ger en timme och fyra sekunder... nej vänta det hjälper inte här för jag kommer att ha timmar och sekunder som exponentielleras? O andra sidan har du skrivit 28 i exponent, som är 4 gånger 7...

$2^{7}$blir nu 2 timmar och 8 sekunder. Måste jag upphöja detta i 4?

2. Haha detta är $(90+2)^{8}$? Den sista siffra måste vara $2^{8}$ I think? Dvs (25)6?

3. Jag ska använda The Force och dela en miljard med 7 och sina minions. 1 000 000 000/ 700 000 000, lämnar en rest på 300 000. Om jag tar en 280 000 chunk är det 20 000 kvar, -14 000 blir det 6 000, minus 4 900 blir det 1 100, minus 1050 blir 5, dvs tisdag +5 som är söndag. Joculator skulle säkert haft delat med negativa modulogrejer men jag vågar inte. Jag hoppas att jag har inte använt The Force för ingenting...

3. Watch the magic now:

Nu har jag kollat the magic och försökte göra om det, och det finns en breaking point:

Jag vet inte om det är potens reglerna eller jättesumman (capital sigma) jag är inte med.

• På hur många sätt kan fem hockeyspelare väljas utav de 13 i laget, om alla har olika positioner på isen?
• På hur många sätt kan samma hockeyspelare väljas i fråga om vilka som står på prispallen?
• Bevisa den kombinatoriska räkneregeln ovan.
• Fyra flickor och fyra pojkar ska väljas till elevrådet. Det finns 60 elever, 50/50 flickor och pojkar. På hur många sätt kan elevrådet väljas? (Alla har samma platser)
• Klantssons målerifirma målar staket. Du kan välja på blått, rosa, gult, rött, och grönt. På hur många sätt kan staketet målas? (Mycket svår uppgift)

1. I första frågan spelar deras position en roll.

Dvs att vi har:

$\frac{n!}{(n-r)!}=\frac{13!}{8!}=13*12*11*10*9= mycket$

2. I andra fråga hur de sitter på banken spelar noll roll:

$\frac{n!}{r!(n-r)!}=\frac{13!}{5!8!}=\frac{13*\cancel{12}*11*\cancel{10}*9}{\cancel{5}*\cancel{4}*\cancel{3}*\cancel{2}*1}= mindre än mycket = 1287$

3. Det har ni bevisat för mig (du, Stokastisk och Albiki bland annat) i en annan tråd och jag kommer ihåg vag att välja alla flickor i en klass är sak samma som välja bort alla pojkar. Måste fundera och återkomma.

4. $\frac{30!}{4!\left(30-4\right)!}\times \frac{30!}{4!\left(30-4\right)!}?$ Eftersom detta är kombinatorisk och att varje val av flikor öppnar en ny möjlig val för pojkar?

${\left(\frac{\cancel{30}\cancel{10}5*29*7*\cancel{28}*27}{\cancel{4}*\cancel{3}*\cancel{2}*1}\right)}^2= {\left(35*29*27\right)}^2= väldigt mycket$

5. Svaret är säkert 5, även om man måste ta hänsyn till vem egentligen som bo där? Du vill säkert att jag skriver på kombinatorisk? Är det $\left(\begin{array}{c}5\\ 1\end{array}\right)$ ? $\left(\frac{5!}{4!(5-1)!}\right)$? Eller är det en permutation, eftersom $Barbiehus \ne Rödsläkterhus$?

Smutstvätt skrev :

Exempeluppgifter:

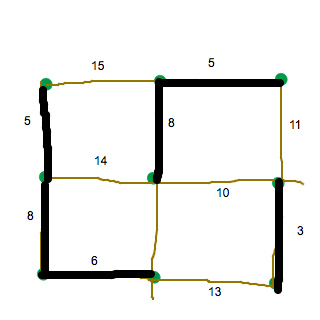
1. Går det att hitta en Eulerväg i figurerna nedan? Går det att hitta en Hamiltonväg? Går det att hitta några cykler? Varför/varför inte?

En Eulerväg är möjligt när max 2 noder har udda valens sa du. Och en Eulercykel är möjligt när alla noder har en jämn valens sa du.

Så jag hittar 3 som har 3 valens, dvs att Eulerscykel och Eulerväg är omöjliga.

En Hamiltonväg går att hitta, men inte en cykel för vi har en enstaka räkare på vänster.

Där måste finnas en Eulersväg och cykel:

En Hamilton ser däremot omöjligt, eftersom det finns ju två nöder som ''spelar tullverket'' om vi vill fortsätta vidare?

Hitta figurens minimalt uppspännande träd. Hur mycket kostar det?

Den sista såg ut mycket lättare att kolla på än att göra själv! Jag hittar 49?

Hoppsan jag måste fortsätta lite senare....

Jag tackar igen så mycket för allt tid du sätt på att göra detta tråd!!

---

Differentialekvationer:

• Diffar med villkor: 
  
  $$\begin{gathered} y\text{'}+5y=0 \\ y\text{'}\left(0\right)=4 \\ y\left(0\right)=3 \end{gathered}$$
  
  Använd standardlösningen för diffar av första graden, och sätt in villkoren för att få ut en exakt lösning.

Critical error system:

Jag hitar att b=4 och c=3, men a körde jag fast.

EDIT: andra critical fail!

ntomast80 skrev :

Otroligt snyggt Smutstvätt! Tvätten är skinande ren 2018!

dajamanté, förslår att du börjar med att bevisa den klassiska Gauss-formeln med induktionsbevis:

$1+2+3+...+(n-1)+n = \frac{n(n+1)}{2}$

Jag lovar. När jag har börjat förstå saken.

(Jag citerar inte för allas skull, det räcker med två milslånga inlägg i tråden. :D

• 39 st. Det stämmer.
• Nja, nu har det blivit knas i den blå bubblan. Hur många är det totalt som tagit med sig skidor?
• Tvätten är smutsig igen: jag är usel på kongruensräkning, och bestämmer därför att enheten är minuter istället för sekunder. I AM GOD!
  
  Tänk dig kongruens som ett snurrande hjul. Klockan räknar ned medan dygnen snurrar för fullt; det är (mod 24). När dygnen är slut börjar timmarna räkna ned; det är mod (60). När timmarna är slut har vi en liten mängd minuter kvar. Först behöver vi ta reda på hur många minuter som blir över:
  
  $$\begin{gathered} 2^{28} (mod 60) \\ {2}^{7·4}=\left(128{)}^4 \\ \right(128{)}^4 (mod 60)\equiv 8^4 (mod 60) \\ {64}^2 (mod 60)\equiv 4^2 (mod 60) \end{gathered}$$
  
  Det blir alltså 16 minuter över. Då är frågan hur många timmar det handlar om. Eftersom tiden är skriven i minuter måste vi först få fram antalet timmar, vilket innebär att vi måste bry oss om kvoten. :( 
  
  $\frac{2^{28}}{60}=\frac{2^2·2^{14}}{2·2·15}=\frac{2^{14}}{15}$
  
  Som sagt, tvätten är kolsvart. Jag tog detta på miniräknaren. Vi har redan sett att timmarna inte går jämnt ut, och vi kommer därför att få decimaler. För att undvika detta kan de sexton minuterna subtraheras från början, eller så räknar vi bara bort decimalerna genom att avrunda nedåt till närmaste heltal. Var dock noggrann med att redovisa detta. Då får vi 1092 timmar, som ska räknas med (mod 24), eftersom det är 24 timmar per dygn.
  
  $$\begin{gathered} \frac{1092}{24}=2·2·3·7·13 (mod 24)\equiv \\ 26 (mod 24)·42 (mod 24)\equiv 12 \end{gathered}$$
  
  Det blir alltså tolv timmar över. Om jag räknat rätt borde klockan då vara 03:16. 
• Det fungerar utmärkt. Ett sätt är annars att dividera med tio och titta på decimalsiffran, vilket är samma sak som att titta på resten (mod 10). 
  
  ${92}^8 (mod 10)\equiv 2^8 (mod 10)\equiv 6 (mod 10)$
• Varför dividerar du med 700 000 000? Hur många dagar är det per vecka i Frankrike?!
  
  $$\begin{gathered} {10}^9 (mod 7)\equiv 3^{9 }(mod 7) \\ {3}^{3·3}={27}^3 \\ 27 (mod 7)\equiv (-1) \\ (-1{)}^3=-1 \\ {10}^{9 }(mod 7)\equiv 6 \end{gathered}$$
  
  Det borde alltså vara måndag om en miljon dagar. Du kanske faktiskt har utnyttjat The Force i onödan.
• Jag var lite otydlig där; de där raderna har inte direkt med varandra att göra. Jag utvecklar endast VL på den raden. 
• Ser bra ut.
• Mycket bra!
• Har vi? Okej, if you say so. 
  
  Ja, mycket bra! Du kan egentligen tänka "Hur många sätt kan vi välja flickorna på" gånger "hur många sätt kan vi välja pojkarna på", men resultatet blir detsamma.
• Nu inser jag att jag glömt att skriva att det är tolv plankor. Jaja. Detta är en krånglig uppgift, problemet är att vi kan ha alltifrån tolv rosa plankor, till två av varje så långt det räcker. Eftersom ordningen inte spelar någon roll, kan vi tänka att vi sorterar alla plankor med samma färg tillsammans. Vi tänker sedan att vi delar av de fem färgerna med fyra vita plankor som avdelare. Dessa plankor måste räknas in i antalet plankor. Totalt får vi då 16 plankor. På hur många sätt kan vi placera dessa fyra vita plankor bland de 16? Alla vita plankor är likadana.
• Mycket bra, allt är korrekt.
• Det stämmer bra!
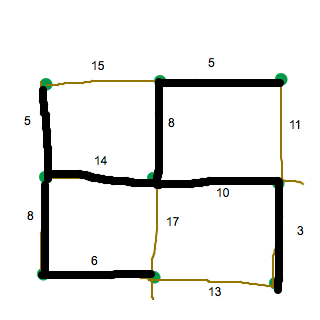
• Det ser bra ut, förutom 17-sträckan. Där får du en cykel. Det går också att välja den andra 8-sträckan, men det är en petitess.

dajamanté skrev :

---

Differentialekvationer:

• Diffar med villkor: 
  
  $$\begin{gathered} y\text{'}+5y=0 \\ y\text{'}\left(0\right)=4 \\ y\left(0\right)=3 \end{gathered}$$
  
  Använd standardlösningen för diffar av första graden, och sätt in villkoren för att få ut en exakt lösning.

Critical error system:

Jag hitar att b=4 och c=3, men a körde jag fast.

Nu blev det lite Kapten Knas här. När du har villkor behöver du inte ansätta en funktion. Det gör du när HL inte är lika med noll. 

Okej, jag ser nu att jag verkligen inte tänkte igenom denna uppgift ordentligt. Utgå bara ifrån att y(0) = 3. 

$$\begin{gathered} y\text{'}+5y=0 \\ y=C{e}^{-5x} \\ y\left(0\right)=C{e}^0=3\Rightarrow C=3 \\ y=3e^{-5x} \end{gathered}$$

Nja, nu har det blivit knas i den blå bubblan. Hur många är det totalt som tagit med sig skidor?

Det blir 25 skitstövlar. Mina skills för huvudräckning har skenat igen.

Tvätten är smutsig igen: jag är usel på kongruensräkning, och bestämmer därför att enheten är minuter istället för sekunder. I AM GOD!

GOD just granted me 60 times more life! YOUHOU!

Nu fortsättar jag med trådet...

Smutstvätt skrev :

Det fungerar utmärkt. Ett sätt är annars att dividera med tio och titta på decimalsiffran, vilket är samma sak som att titta på resten (mod 10). ${92}^8 (mod 10)\equiv 2^8 (mod 10)\equiv 6 (mod 10)$

Hmmm så du har delat 92 med 10? Varför får man göra så? Det är ju inte 92 utan 92 upphöjd i 8?

Varför dividerar du med 700 000 000? Hur många dagar är det per vecka i Frankrike?!$$\begin{gathered} {10}^9 (mod 7)\equiv 3^{9 }(mod 7) \\ {3}^{3·3}={27}^3 \\ 27 (mod 7)\equiv (-1) \\ (-1{)}^3=-1 \\ {10}^{9 }(mod 7)\equiv 6 \end{gathered}$$

Det borde alltså vara måndag om en miljon dagar. Du kanske faktiskt har utnyttjat The Force i onödan.

Nej, det finns inte lika många dagar i en franska vecka en i en Smaragdalenas dygn.... Men jag menar att jag har tagit bort allt skit som är delbart med 7 från en miljard.

Och tisdag  + 5 dagar blir måndag. Jag har omitterat att 5 dagar har passerat efter tisdag. The Force dög, men inte min huvud räckning som vanligt - men helt rätt, man får inte använda The Force när man lär sig modulo räckning. Men nu ska jag kolla på din mod beräckning o fortsätta tråden. 

PS: GOD är mycket lekful med space-time idag :). Är den en miljon eller en miljard dagar?

Smutstvätt skrev :

$$\begin{gathered} y\text{'}+5y=0 \\ y=C{e}^{-5x} \\ y\left(0\right)=C{e}^0=3\Rightarrow C=3 \\ y=3e^{-5x} \end{gathered}$$

Det ser bra ut! Jag hade försökt med en exponentiell funtion också men hittade inget vettig, pga 4:an. Alltså det blev en okontrollbar konstant.

Edit: Gaypride planckor måste jag återkomma till tyvärr. Jag trodde att du var ironisk när du sa att den var en mycket svår uppgift. Men du menade allvar!

God morgon!

Nu är jag kanske med, ångående:

Bevisa den kombinatoriska räkneregeln ovan. 

Som var $\left(\begin{array}{c}n\\ r\end{array}\right)=\left(\begin{array}{c}n\\ n-r\end{array}\right)$

Principen är att det är lika många sätt att välja A-grejer från en grupp från att välja bort B-grejer (given att vi bara har A och B grejer?) från samma grupp. Och att det är kombinatorik, så alla dubbel möjliga val måste sorteras bort?

$\left(\begin{array}{c}n\\ r\end{array}\right)=\frac{n!}{r!(n-r)!}$ och $\left(\begin{array}{c}n\\ n-r\end{array}\right)=\frac{n!}{(n-r)!(n-(n-r\left)\right)!}=\frac{n!}{(n-r)!(n-n+r)!}=\frac{n!}{r!(n-r)!}$, som är lika!

Det ser bra ut, förutom 17-sträckan. Där får du en cykel. Det går också att välja den andra 8-sträckan, men det är en petitess.

Du menar att jag borde ha valt den här 10-sträckan?

Vad innebär det att det blev en cykel?

Typiska uppgifter:

• y''+ y' +5y = 2x + 7
• y' + 2y = x^2+3x-4
• y'-3y = cos2x

1. Det är en första grad polynom man söker (eftersom det finns ingenting av andra grad på höger sida)?

$y''=0$

$y(a)+5(ax+b)=2x+7$

$ya+5ax+5b=2x+7$

Matchning.com ger:

$\left\{\begin{array}{l}5a=2\\ a+5b=7\end{array}\right.$

$\left\{\begin{array}{l}a=\frac{2}{5}\\ \frac{2}{5}+5b=7\end{array}\right.$

Detta ger $y=\frac{2}{5}x+\frac{33}{25}$

2. y' + 2y = x^2+3x-4

Error converting from LaTeX to MathML

Error converting from LaTeX to MathML

Detta ger:

$\left\{\begin{array}{l}\begin{array}{l}b+2c=-4\\ ax+2bx=3x\end{array}\\ 2a{x}^2=x^2\end{array}\right.$

$$\begin{gathered} a=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. \\ b=\frac{3-{\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}}{2}=1.25 \\ c=-\raisebox{1ex}{$19$}\!\left/ \!\raisebox{-1ex}{$8=2.375$}\right. \end{gathered}$$

3.y'-3y = cos2x

De brukar vara snälla!

 y'(-aksinkx + bcoskx)-2(acoskx + bsinkx)= cos2x

$\left\{\begin{array}{l}b\sin kx-a\sin kx=0, så a=b\\ b-a=1, så b=2\end{array}\right.$

f(x)= cos2x + 2sin2x... och det blir fel!!!!!

• Kombinatoriken är rätt!
• Nej, jag menar 8-sträckan på precis motsatt sida, längst till höger. Att det blir en cykel innebär att då kan gå runt runt runt utan att lyfta pennan. Då är det inget träd. I algoritmen ingår att en måste undvika cykler till varje pris. I en cykel finns det två kopplingar till samma punkt; det är dyrt och bidrar inte med mer än en koppling skulle ha gjort.
• Börja med att hitta den allmänna lösningen för dessa ekvationer. I den första har du glömt y'' +y' + 5y. Då blir det knas i ekvationssystemet.

Usch jag ser nu att det är en hel del LaTex errors :(.

Du menar att y'' +y' + 5y är en andra gradare?

dajamanté skrev :

Usch jag ser nu att det är en hel del LaTex errors :(.

Du menar att y'' +y' + 5y är en andra gradare?

Nej, men du måste lösa y'' + y' + 5y = 0 först. Ändra den ekvationen till y'' + -4y' + 4y = 2x + 7, det blir lättare att lösa.

Smutstvätt skrev :

dajamanté skrev :

Usch jag ser nu att det är en hel del LaTex errors :(.

Du menar att y'' +y' + 5y är en andra gradare?

Nej, men du måste lösa y'' + y' + 5y = 0 först. Ändra den ekvationen till y'' + -4y' + 4y = 2x + 7, det blir lättare att lösa.

y''+y'+5y=0?

Är y'' fortfarande noll?

Måste jag tänka första eller andra gradare?

Har du lärt dig att lösa homogena differentialekvationer av andra graden? Vi tar två olika exempel:

a) y'' - 2y' - 3 = 0
b) y'' + 3y + 9 = 0

a) Antag att lösningen är y = Ae^rx. 

$$\begin{gathered} y\text{'}=Ar{e}^{rx} \\ y\text{'}\text{'}=A{r}^2{e}^{rx} \\ A{r}^2{e}^{rx}-2Ar{e}^{rx}-3A{e}^{rx}=0 \end{gathered}$$

Lös ut Ae^rx:

$A{e}^{rx}(r^2-2r-3)=0$

Andragradsekvationsdelen brukar kallas för en karaktäristisk ekvation. Denna kan lösas med kvadratkomplettering, PQ eller whatever. Rötterna är -3 och +1. Detta sätter vi in i vår ursprungsekvation. Den hela lösningen blir då:

$y=A{e}^{-3x}+A{e}^x$

b) Här har vi en dubbelrot. Början (med ansättning och dylikt) är densamma, men när vi fått ut lösningen (r = -3), är lösningen på formen $y=(Ax+B)e^{rx}$. I vårt fall blir det $y=(Ax+B)e^{-3x}$. 

För partikulärlösningen behöver du endast ansätta en ekvation av första graden. 

Allt jag kan om matte 5 är på detta tråd :)!

Ok, jag måste nog läsa om detta och meditera (zzzz.......) ett stund.

EDIT: vänta nu...

Lösningarna blir exponenter? Varför och varför plussas två $Ae^{rx}$?

Det är målet!

Ja, eftersom vi antog att den allmänna lösningen var y = Ae^rx. Varför de plussas? Eftersom det finns två olika lösningar på r i den karaktäristiska ekvationen.

Jag trodde att vi skulle ha en lösning 1 och en lösning 2, som för andragradare.

Så när du skriver y''+ y' +5y = 2x + 7, det är egentligen en exponentiell ekvation som varje y beskriver?

En liten detalj i sammanhanget, men är det inte så att tomma mängden betecknas $\left\{\right\}$ eller $\varnothing$, snarare än $\{\varnothing \}$ ? Om man skriver $\{\varnothing \}$ så har man beskrivit en mängd med ett enda element, där det enda elementet är den tomma mängden. Jag tror att det dessutom är potensmängden av den tomma mängden. Denna mängd har kardinalitet 1 (innehåller 1 element), och tomma mängden har kardinalitet 0 (innehåller inga element). $\varnothing =\left\{\right\}$ men $\left\{\right\} \ne \{\varnothing \}$ just för att HL där beskriver en mängd med ett element som är den tomma mängden, alltså $\{\varnothing \}=\{ \{\} \}$.

Apropå kardinalitet; säger man mäktighet på svenska? -- man har åtminstone begreppet "likmäktighet" på svenska som jag inte vet vad det heter på engelska, annat än "same cardinality". Används mäktighet bara i uttrycket "likmäktig", eller kan man använda mäktighet för att beskriva antalet element. Finns det förresten någon ändlig mäktighet som inte går att beskriva som ett naturligt tal? Jag får lite ont i huvudet av att försöka föreställa mig en sån mängd.

Saxat ur matteboken:

Aha, nej det blir en lösning med två termer.

Ja, lösningen till den allmänna ekvationen är exponentiell, ja. 

dajamanté, du kanske är redo för att bevisa Gauß formel nu med induktion?

Trots hur det ser ut, jag har inte glömt!

Jag har inte kommit så långt i tänkegången eller i matte 5 bocken än.

Den enda jag kan bjuda på just nu är en geometrisk summa :D

$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}....\frac{1}{n}=\frac{a_1(k^n-1)}{k-1} \frac{\frac{1}{2}({\left({\displaystyle \frac{1}{2}}\right)}^{\infty }-1)}{\frac{1}{2}-1}=\frac{-0.5}{-0.5}=1$

Nu har det väl ändå blivit knas någonstans, Daja? Alla termer är positiva. Ett plus en halv (plus ännu mer positivt), kan ju inte bli ett? Var är du i boken just nu? 

dajamanté skrev :

Trots hur det ser ut, jag har inte glömt!

Jag har inte kommit så långt i tänkegången eller i matte 5 bocken än.

Den enda jag kan bjuda på just nu är en geometrisk summa :D

$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}....\frac{1}{n}=\frac{a_1(k^n-1)}{k-1} \frac{\frac{1}{2}({\left({\displaystyle \frac{1}{2}}\right)}^{\infty }-1)}{\frac{1}{2}-1}=\frac{-0.5}{-0.5}=1$

Det låter bra! Stressa inte.

Din formel ovan ser korrekt ut förutom två saker:

VL: sista termen ska vara: $(\frac{1}{2})^n$

HL: vad är egentligen $a_1$?

Om du direkt jämför VL med HL så ser du att $VL > 1 = HL$ (som det är skrivit nu).

Om jag bara visste... i tal teori tror jag.

Jag förstår inte vad du menar, funkar inte $\frac{a_1\left(k^n-1\right)}{k-n}$, med k=0.5 och n=+$\infty$?

Ah vänta det är inte ens Gauss följd....

tomast80 skrev :

dajamanté skrev :

Trots hur det ser ut, jag har inte glömt!

Jag har inte kommit så långt i tänkegången eller i matte 5 bocken än.

Den enda jag kan bjuda på just nu är en geometrisk summa :D

$1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}....\frac{1}{n}=\frac{a_1(k^n-1)}{k-1} \frac{\frac{1}{2}({\left({\displaystyle \frac{1}{2}}\right)}^{\infty }-1)}{\frac{1}{2}-1}=\frac{-0.5}{-0.5}=1$

Det låter bra! Stressa inte.

Din formel ovan ser korrekt ut förutom två saker:

VL: sista termen ska vara: $(\frac{1}{2})^n$

HL: vad är egentligen $a_1$?

Om du direkt jämför VL med HL så ser du att $VL > 1 = HL$ (som det är skrivit nu).

$a_1$ var 0.5 trodde jag?

$a_1$ är den första termen i den geometriska serien. Vilken är det i detta fall?

Jo, formeln fungerar med rätt värden på parametrarna.

tomast80 skrev :

$a_1$ är den första termen i den geometriska serien. Vilken är det i detta fall?

Neeeeej det var ju 1. Kan jag trolla bort problemet såhär? $1=\frac{1}{2^0}$ och behålla 0.5 som a1 på nåt sätt?

dajamanté skrev :

tomast80 skrev :

$a_1$ är den första termen i den geometriska serien. Vilken är det i detta fall?

Neeeeej det var ju 1. Kan jag trolla bort problemet såhär? $1=\frac{1}{2^0}$ och behålla 0.5 som a1 på nåt sätt?

Det  du kan göra är att sätta $S' = 1+S$ och då börjar $S'$ med $\frac{1}{2}$ stället för $1$. Sedan kan du lägga till $1$ igen på slutet. Lite omständigt, men det går.

tomast80 skrev :

dajamanté skrev :

Visa föregående citat

tomast80 skrev :

$a_1$ är den första termen i den geometriska serien. Vilken är det i detta fall?

Neeeeej det var ju 1. Kan jag trolla bort problemet såhär? $1=\frac{1}{2^0}$ och behålla 0.5 som a1 på nåt sätt?

Det  du kan göra är att sätta $S' = 1+S$ och då börjar $S'$ med $\frac{1}{2}$ stället för $1$. Sedan kan du lägga till $1$ igen på slutet. Lite omständigt, men det går.

Men funkar ageometriska följden i så fall?

Ja, $\lim_{n\to \infty} S' = 1 \Rightarrow$

$\lim_{n\to \infty} S = 1+1=2$

Guud jag är fortfarande inte med.

Jag fortsätter lite till med matteboken, återkommer snart nån gång, eventuellt, till Gausseriet.