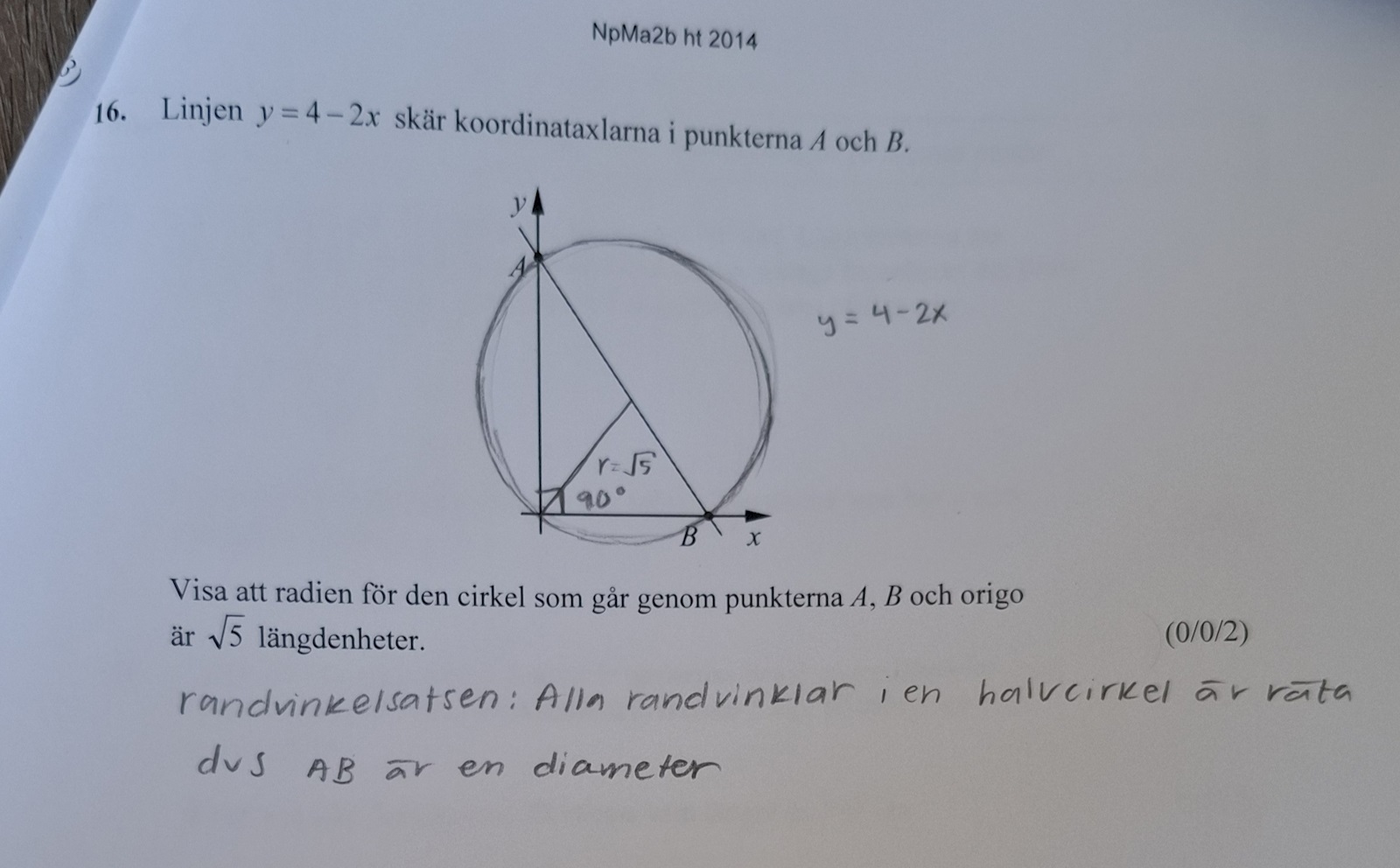
Visa att cirkelns radie är √5
Har lyckats räkna ut kordinaterna för punkterna A och B. Men kommer inget vidare. Förstår inte vart cirkelns radie är? :(((
Rubrik ändrad från "Matte:(" till nuvarande. En beskrivande rubrik underlättar för de som svarar, och hjälper till att skilja trådar från varandra. Läs gärna mer om rubriksättning här. /Smutstvätt, moderator
Edit: Bilden verkar ha försvunnit av misstag. Här är den igen:

Första gången jag såg den här uppgiften (för några veckor sedan) kom jag inte på hur man skulle lösa den,särskilt om man inte fick använda sig av sådant som man lär sig i Ma3 och senare... Men nu kom jag på det! En av följdsatserna till randvinkelsatsen säger att alla randvinklar i en halvcirkel är räta. Det är en rät vinkel i origo. Detta innebär att linjen AB måste vara en diameter. Kommer du vidare?
Jag ser att det är en uppgift från ett gammalt NP. Hoppas man får A-poäng på den, det tycker jag att man borde!
0/0/2, d.v.s. 2 A-poäng.
Här är en annan lösning, om man inte känner till randvinkelsatsen.
Cirkelns centrum C måste ha samma avstånd (radien) till punkterna A, B och O.
Alla punkter som har samma avstånd till punkterna O och B ligger på den vertikala gröna linjen, dvs på mittpunktsnormalen till segmentet OB. På samma sätt ligger alla punkter som har samma avstånd till punkterna O och A på den horisontella gröna linjen, dvs på mittpunktsnormalen till segmentet OA. Cirkelns centrum C måste ligga på skärningen mellan de gröna linjerna, eftersom det är den enda punkt som har samma avstånd till samtliga punkter (A, B och O).
Vi ser att skärningen blir punkten (1, 2). Cirkelns radie är lika med avståndet från origo till punkten C = (1, 2), dvs √12+22=√5.

Smaragdalenas knep är utmärkt, men om en inte kommer på knepet, borde det gå att utgå från cirkelns ekvation här:
(x-a)2+(y-b)2=r2
Vi vet att en av punkterna är origo, vilket ger oss sambandet a2+b2=r2.
En annan punkt är (0,4). Det ger sambandet a2+(4-b)2=r2.
Den tredje punkten är (2,0). Det ger sambandet (2-a)2+b2=r2.
Vi kan kombinera de första två sambanden till ekvationen
b2=(4-b)2b=±(4-b)b=2
Och likaså kan samband ett och tre kombineras till
(2-a)2=a2a=±(2-a)a=1
Insättning av a och b i ekvationen a2+b2=r2 får vi ut att r2=5, och eftersom en radie alltid är positiv får vi att radien är r=√5 le.
Man har inte lärt sig ekvationen för en cirkel när man läser Ma2. Däremot har man lärt sig randvinkelsatsen, så det är därför jag tror att det är den som skall användas (eller i alla fall att det är så man har tänkt).
Smaragdalena skrev:Man har inte lärt sig ekvationen för en cirkel när man läser Ma2. Däremot har man lärt sig randvinkelsatsen, så det är därför jag tror att det är den som skall användas (eller i alla fall att det är så man har tänkt).
När man läser bedömningsmallen framgår det med tydlighet att randvinkelsatsen, eller någon form av bevis att AB är diameter, måste ingå för högsta poäng.
Aha, attans! Jag hade för mig att cirkelns ekvation lärdes ut i Ma2. :(
Smutstvätt skrev:Aha, attans! Jag hade för mig att cirkelns ekvation lärdes ut i Ma2. :(
Cirkelns ekvation har till och med tagits bort från matte 3
tack för all hjälp!! tror jag förstog!!
Trinity2 skrev:Smaragdalena skrev:Man har inte lärt sig ekvationen för en cirkel när man läser Ma2. Däremot har man lärt sig randvinkelsatsen, så det är därför jag tror att det är den som skall användas (eller i alla fall att det är så man har tänkt).
När man läser bedömningsmallen framgår det med tydlighet att randvinkelsatsen, eller någon form av bevis att AB är diameter, måste ingå för högsta poäng.
Vad löjligt, PATENTERAMERAs lösning är enkel och tydlig utan att använda att AB är diameter.
Vad löjligt, PATENTERAMERAs lösning är enkel och tydlig utan att använda att AB är diameter.
Om någon elev skulle ge PATENTERAMERAs lösning utan att man hade gått igenom cirkelns ekvation, så skulle en vettig mattelärare ge full poäng även utan randvinkelsatsen. Bedömningsanvisningarna kan inte förutse 100 % av alla tänkbara elevlösningar.
Man behöver inte cirkelns ekvation för att använda PATENTERAMERAs lösning.
Min slutsats gäller ändå. PATENTERAMERA skulle ha fått full poäng.
joculator skrev:Trinity2 skrev:Smaragdalena skrev:Man har inte lärt sig ekvationen för en cirkel när man läser Ma2. Däremot har man lärt sig randvinkelsatsen, så det är därför jag tror att det är den som skall användas (eller i alla fall att det är så man har tänkt).
När man läser bedömningsmallen framgår det med tydlighet att randvinkelsatsen, eller någon form av bevis att AB är diameter, måste ingå för högsta poäng.
Vad löjligt, PATENTERAMERAs lösning är enkel och tydlig utan att använda att AB är diameter.
Du får framföra dina synpunkter till skolverket.
Jag skulle ha givit full poäng och inte sagt nånting till Skolverket.
Nej asså jag fattar inte fortfarande. Hur kommer informationen att vinkeln vid origo är 90 grader hjälpa mig räkna ut radien?