Mathematica - Summor

Vad menar du med att funktionen blir 1? Vad blir $\frac{(-1{)}^{k+1}}{2k-1}$när du sätter in t.ex. k = 2?

Laguna skrev:

Vad menar du med att funktionen blir 1? Vad blir $\frac{(-1{)}^{k+1}}{2k-1}$när du sätter in t.ex. k = 2?

 K=1 i nedre delen, dum som jag är så hade jag fått för mig att man endast skulle sätta det k i funktionen för att räkna ut summan enkelt, men så är ju uppenbarligen inte fallet. Jag editar posten. Hur som helst, så behöver jag hjälp med hur man går tillväga för att lösa ekvationen.

Du har förmodligen missat någon parentes eller använt funktionen Sum[] fel när du matat in din summa. För de 50 första termerna ser det ut så här:

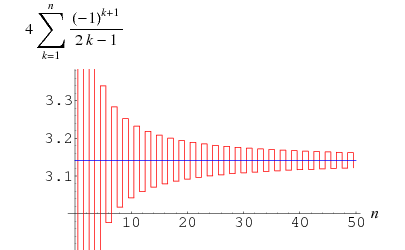
Om dragen till oändligheten är det den berömda Gregory-Leibniz-summan, du kan läsa mer om den här: http://mathworld.wolfram.com/GregorySeries.html

Ska du använda en web-version av Mathematica? Vilken sida ska du använda? Det svåra borde bara vara att hitta rätt sida och sedan mata in uttrycket korrekt. Grejen med flyttal är att Mathematica räknar ut summan exakt, så du får ett oerhört stort bråk, som du får göra till decimaltal. Det finns säkert flera metoder, men en är att skriva 4 som decimaltal: 4.0.

Här är sidan jag använde, med en enklare formel: https://www.wolframalpha.com/input/?i=sum+1%2Fk,+k%3D1+to+10

jag kollade in några standard expansioner och serien börjar med $1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9} osv$ vilket är ganska likt $\frac{1}{1+x}=1-x+x^2-x^3+x^4...$ Jag vet inte riktigt hur man skulle kunna gå vidare här ifrån

Guggle skrev:

Du har förmodligen missat någon parentes eller använt funktionen Sum[] fel när du matat in din summa. För de 50 första termerna ser det ut så här:

Om dragen till oändligheten är det den berömda Gregory-Leibniz-summan, du kan läsa mer om den här: http://mathworld.wolfram.com/GregorySeries.html

 Aha okej. Då den är dragen till 1000 så borde det bli ett extremt stort tal som Laguna skrev. Ska jag först räkna ut med Sum[] för att sedan ta det stora svaret som: N[svaret]? 

Om man nu är intresserad av att beräkna när serien går mot oändligheten (vilket inte är vad uppgiften frågar efter, men det kan väl vara kul ändå) kan man använda sig av den geometriska serien med $-x^2$:

$\displaystyle\frac{1}{1+x^2}=\sum_{n=0}^{\infty} \left(-x^2\right)^n$

Integrerar man sedan båda sidor får man arctan-integralen i vänsterled:

$\displaystyle\int\frac{1}{1+x^2}\ dx=\int\sum_{n=0}^{\infty}\left(-x^2\right)^n\ dx$

$\displaystyle\arctan\left(x\right)=\sum_{n=0}^{\infty}\dfrac{(-1)^n}{2n+1}x^{2n+1}$

och sätter man in $x=1$ och trixar med lite gränser får man:

$\displaystyle\arctan\left(1\right)=\sum_{k=1}^{\infty}\frac{(-1)^{k+1}}{2k-1}$

AlvinB skrev:

Om man nu är intresserad av att beräkna när serien går mot oändligheten (vilket inte är vad uppgiften frågar efter, men det kan väl vara kul ändå) kan man använda sig av den geometriska serien med $-x^2$:

$\displaystyle\frac{1}{1+x^2}=\sum_{n=0}^{\infty} \left(-x^2\right)^n$

Integrerar man sedan båda sidor får man arctan-integralen i vänsterled:

$$\displaystyle\int \frac{1}{1+x^2}\ dx=\int \sum_{n=0}^{\infty} \left(-x^2\right)^n\ dx$$

$\displaystyle\arctan\left(x\right)=\sum_{n=0}^{\infty}\dfrac{(-1)^n}{2n+1}x^{2n+1}$

och sätter man in $x=1$ och trixar med lite gränser får man:

$\displaystyle\arctan\left(1\right)=\sum_{n=1}^{\infty}\frac{(-1)^{k+1}}{2k-1}$

 Okej, har du något tips till min fråga om själva uppgiften?

Gör som du föreslår i ditt föregående inlägg:

Använd Sum[] för att beräkna summan och använd sedan N[] för att få en decimalapproximation.

AlvinB skrev:

Gör som du föreslår i ditt föregående inlägg:

Använd Sum[] för att beräkna summan och använd sedan N[] för att få en decimalapproximation.

 Aha okej! En fråga bara, vad gör 4:an framför summationssymbolen? Multiplicerar den med svaret med 4, eller är det mer komplicerat än så?

kwalker2 skrev:

Aha okej. Då den är dragen till 1000 så borde det bli ett extremt stort tal som Laguna skrev. Ska jag först räkna ut med Sum[] för att sedan ta det stora svaret som: N[svaret]? 

Ja,

4*Sum[(-1)^(k + 1)/(2*k - 1), {k, 1, 1000}]

Ger dig summan. Om svaret hamnar i t.ex. Out[3] skriver du

N[%3]

För att få ett numeriskt värde på svaret.

Du kan också skriva 4*Sum[(-1)^(k + 1)/(2*k - 1), {k, 1, 1000}]//N

För att få ett numeriskt värde direkt.

Limit[4*Sum[(-1)^(k + 1)/(2*k - 1), {k, 1, N}], N -> \[Infinity]]

Ger dig den exakta summan dragen till oändligheten.

kwalker2 skrev:

AlvinB skrev:

Gör som du föreslår i ditt föregående inlägg:

Använd Sum[] för att beräkna summan och använd sedan N[] för att få en decimalapproximation.

 Aha okej! En fråga bara, vad gör 4:an framför summationssymbolen? Multiplicerar den med svaret med 4, eller är det mer komplicerat än så?

 Som Guggle nämner ska du bara multiplicera summan med den, ja. Du får även samma svar om du multiplicerar in den med uttrycket i summan eftersom multiplikation är distributivt med avseende på addition.

Anledningen till att man multiplicerar summan med fyra blir uppenbar när du kollar på decimalutvecklingen. Det är nämligen så att summan går mot en välkänd konstant delat med fyra, och då multiplicerar man med fyra för att man ska få bara konstanten.

Då förstår jag! Det var instruktionen med flyttalet jag inte förstod som strulade till det för mig, men nu har jag fått grepp om det. 

Det jag gjorde var att jag skapade en variabel som hette sumLargeValue som sattes lika med 4 * Sum[Funktionen]. När jag sedan använde N[] så skrev jag bara in variabeln inom parameterna. Så i stort sett som en variabel inom programmering. 

Tack så mycket för hjälpen :)

kwalker2 skrev:

Laguna skrev:

Vad menar du med att funktionen blir 1? Vad blir $\frac{(-1{)}^{k+1}}{2k-1}$när du sätter in t.ex. k = 2?

 K=1 i nedre delen, dum som jag är så hade jag fått för mig att man endast skulle sätta det k i funktionen för att räkna ut summan enkelt, men så är ju uppenbarligen inte fallet. Jag editar posten. Hur som helst, så behöver jag hjälp med hur man går tillväga för att lösa ekvationen.

 kwalker2, det står i Pluggakuten att du inte frår "redigera ihjäl" ett inlägg  när det har blivit besvarat - nu är ju Lagunas inlägg obegripligt, eftersom det försvunnit från ditt inlägg. Däremot är det tillåtet att stryka över det som har blivit fel och skriva dit det rätta. /moderator