Matematisk Statistik, Normalfördelningsfunktion, 4.14e (K.Vännman)
Hej! Har en fundering kring följande fråga: (gäller specifikt e)
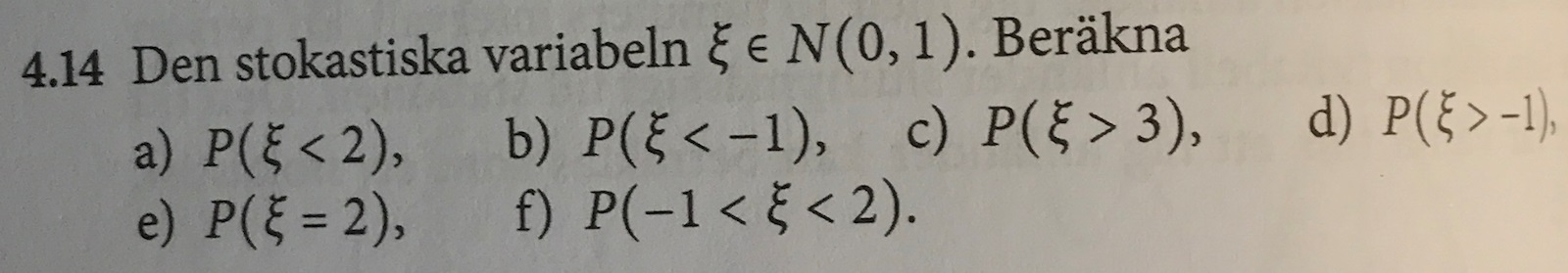
Jag har gjort följande:
Där "normalpdf" är en funktion på min TI-82a som gäller för diskret normalfördelning. Enligt facit ska svaret bli 0 vilket det blir om man istället använder som man får genom:

vilket då tar ut varandra.
Min fråga är då, har jag gjort fel i mitt antagande om att det är en diskret variabel och bör vara kontinuerlig eller bör jag använda istället och undvika miniräknaren som i övriga upp.g. gett rätt svar?
Utan större statistiska kunskaper inser man att sannolikheten för en händelse är integralen av kurvan över den delmängd av utfallsrummet som händelsen utgör. Om händelsen består av ett enda utfall i ett rum med oändligt många utfall (stokastisk betyder väl kontinuerlig?) så är integralen = 0. Jfr med arean av en rektangel med basen =0. Detta stöds också av att Lebesgue-måttet av en punkt =0.
Tomten skrev:Utan större statistiska kunskaper inser man att sannolikheten för en händelse är integralen av kurvan över den delmängd av utfallsrummet som händelsen utgör. Om händelsen består av ett enda utfall i ett rum med oändligt många utfall (stokastisk betyder väl kontinuerlig?) så är integralen = 0. Jfr med arean av en rektangel med basen =0. Detta stöds också av att Lebesgue-måttet av en punkt =0.
Ah, Tack!

