Matematisk Statistik, Fördelningsfunktion, 4.1 (K.Vännman)

F(8) är sannolikheten att $\xi < 8$.

Laguna skrev:

F(8) är sannolikheten att $\xi < 8$.

aha, hur blir $F(\xi =8)$?

Hur räknar du ut sannolikheten att $\xi > 8$?

Laguna skrev:

Hur räknar du ut sannolikheten att $\xi > 8$?

$\xi >8=1-F\left(8\right)$

Hur mycket blir det kvar för $\xi =8$ då?

Till ChocolateTerrain:

Medan du funderar på Lagunas filosofiska fråga,
skulle du kunna bestämma fördelningsfunktionen
och rita dess graf.

Då klarnar nog ett och annat.

Laguna skrev:

Hur mycket blir det kvar för $\xi =8$ då?

humm, gjorde såhär:

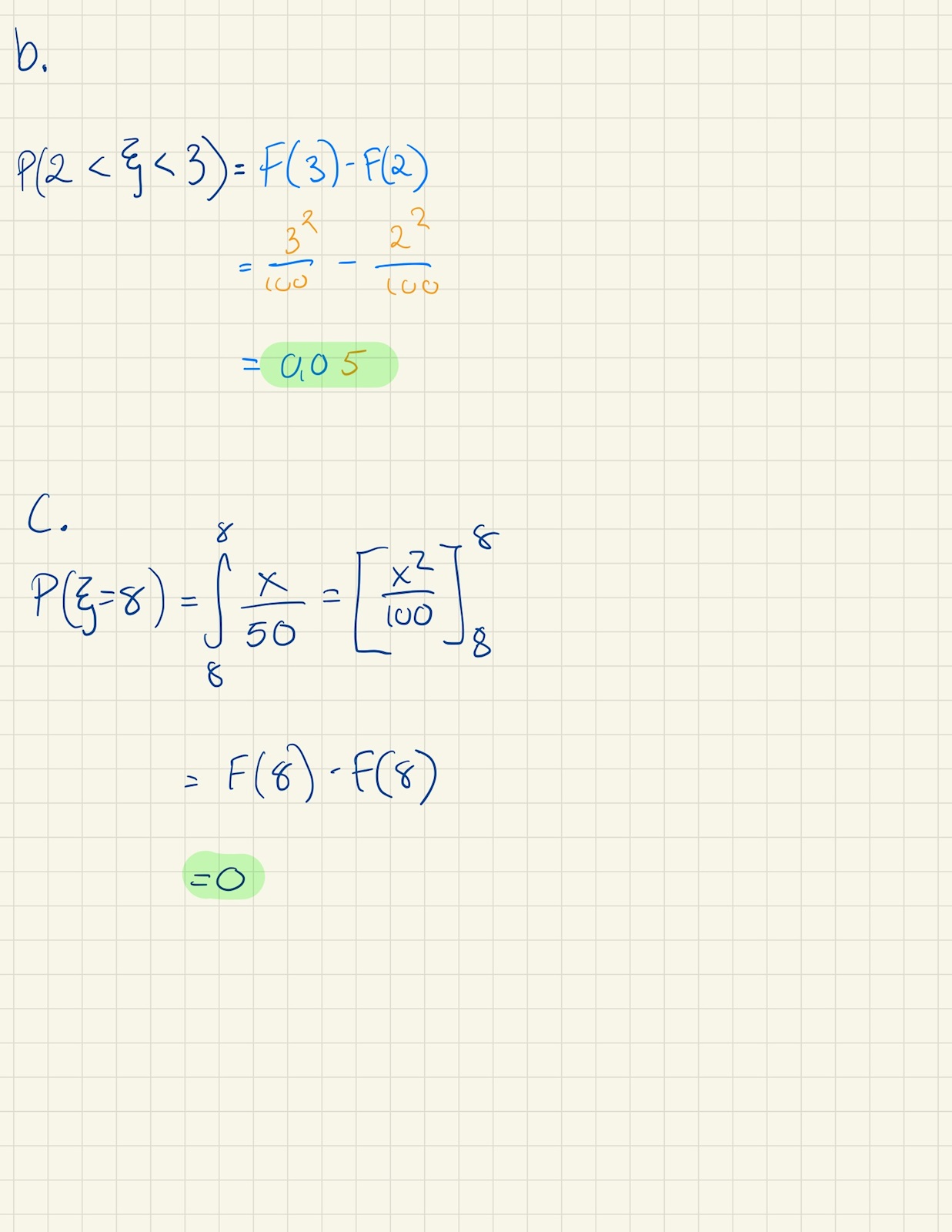
Arktos skrev:

Till ChocolateTerrain:

Medan du funderar på Lagunas filosofiska fråga,
skulle du kunna bestämma fördelningsfunktionen
och rita dess graf.

Då klarnar nog ett och annat.

ah! Japp släppte när jag riktade fördelningsfunktionens graf;

Glömde bort att de var integraler som jag höll på med och eftersom det är en punk så är bredden=0 dvs, $"höjd"·0=0$Tack!

Men var är grafen?
Är funktionen bara definierad för heltalsvärden på  x ?
Vad händer mellan de röda punkterna?

Arktos skrev:

Men var är grafen?
Är funktionen bara definierad för heltalsvärden på  x ?
Vad händer mellan de röda punkterna?

Funktionen är väl definierad för 0<x?    Mellan de röda punkterna antas värden. 

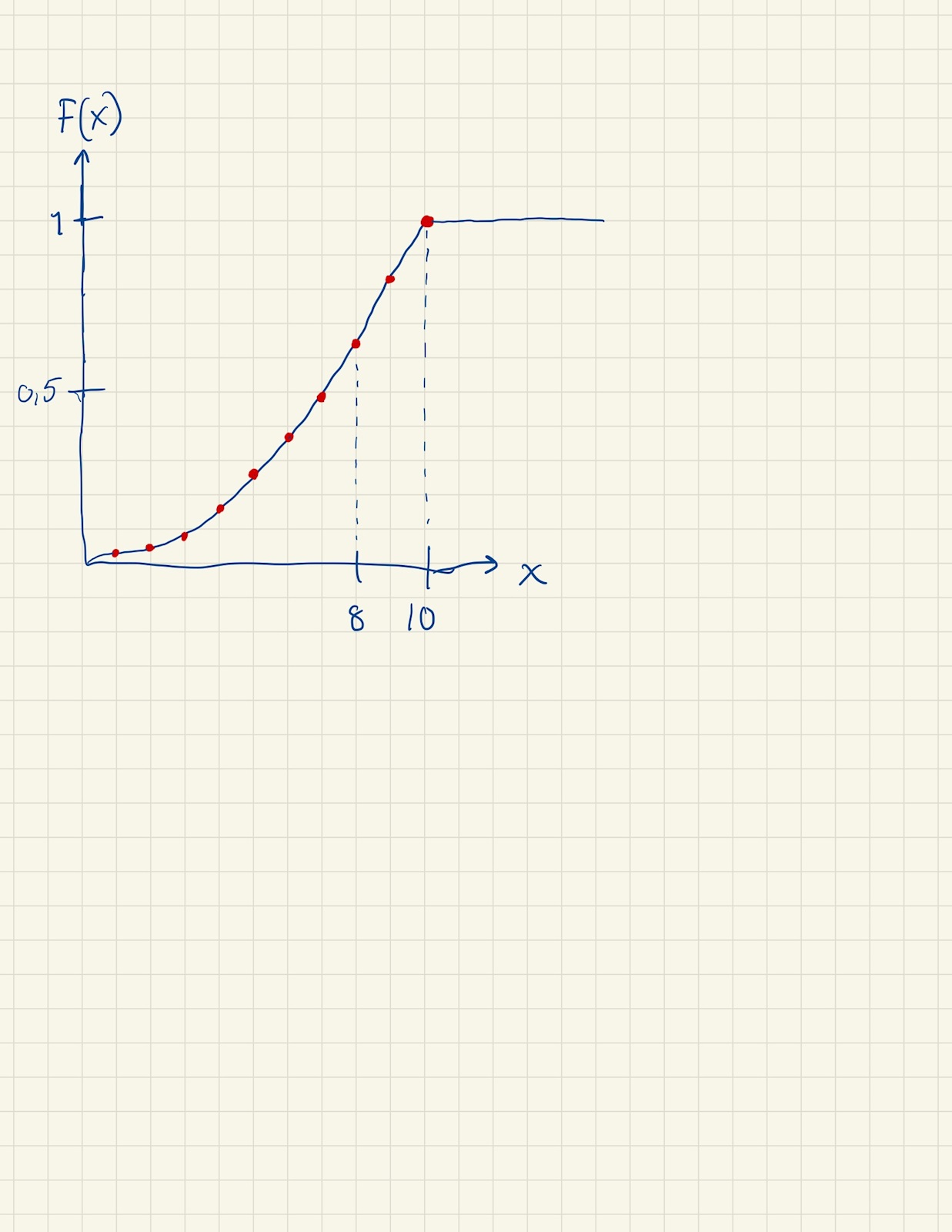
Fördelningsfunktionen är definierad för alla värden på  x  .
Den är lika med  0             för  x < 0 , 
Den är lika med  x²/100    för   0 ≤ x ≤ 10
Den är lika med  1              för  x > 10

Samtidigt är   P(X = x) = 0   för alla värden på  x  .  
[Du har själv visat det för  x = 8 ]
Hur kan det hänga ihop?

Arktos skrev:

Fördelningsfunktionen är definierad för alla värden på  x  .
Den är lika med  0             för  x < 0 , 
Den är lika med  x²/100    för   0 ≤ x ≤ 10
Den är lika med  1              för  x > 10

Samtidigt är   P(X = x) = 0   för alla värden på  x  .  
[Du har själv visat det för  x = 8 ]
Hur kan det hänga ihop?

Pågrund utav att analysens fundamentalsats: $F\left(x\right)={\int }_a^{b}f\left(x\right)dx=F\left(b\right)-F\left(a\right)$

då a=b blir det F(a)-F(a)=0

Det är sant,
men hur kommer det sig att  X  kan anta vilket värde som helst mellan  0  och  10 ,
trots att   P(X = x) = 0   för vart och ett av dessa värden på  x  ?

Arktos skrev:

Det är sant,
men hur kommer det sig att  X  kan anta vilket värde som helst mellan  0  och  10 ,
trots att   P(X = x) = 0   för vart och ett av dessa värden på  x  ?

humm... Nu hänger jag inte riktigt med

Visst är det förbryllande!

Nu blir det filosofiskt.
En omöjlig händelse tilldelar vi alltid sannolikheten  0 .
Att sannolikheten för en händelse är 0 behöver däremot inte betyda att händelsen är omöjlig.

Så är det för kontinuerliga slumpvariabler som denna  (annars får man inte ihop det!)
i motsats till diskreta slumpvariabler (som poäng vid kast med tärning)

Slut från filosofiska hörnet.

Arktos skrev:

Visst är det förbryllande!

Nu blir det filosofiskt.
En omöjlig händelse tilldelar vi alltid sannolikheten  0 .
Att sannolikheten för en händelse är 0 behöver däremot inte betyda att händelsen är omöjlig.

Så är det för kontinuerliga slumpvariabler som denna  (annars får man inte ihop det!)
i motsats till diskreta slumpvariabler (som poäng vid kast med tärning)

Slut från filosofiska hörnet.

hahaha, visst blev det filosofiskt allt, men kommer ta min stund att smälta detta....