Matematisk modellering, metod för att lösa PDE med BV?
Hej!
Frågeställning: 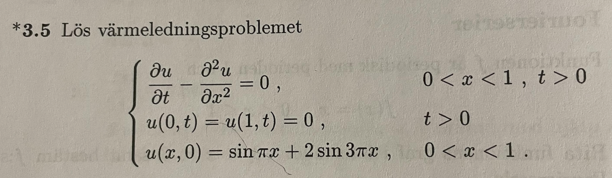
har problem med denna. försökte lösa med variabelseparation men kom endast halvvägs innan jag blev orolig att något blivit fel:

känner mig lite osäker på metoden. vad ska jag göra med begynnelsevillkoret? Ska jag gå vidare och beräkna integralen även om BV är en funktion av x? kände mig relativt säker på metoden för några dagar sedan, men har sedan dess sett så många olika sätt att lösa liknande problem på att jag inte längre kan särskilja höger från vänster.
lösningsförslaget gjorde mig bara mer förvirrad.
Lösningsförslag:


vad är ens entydigheten för fourierserier? det finns ytterst lite (läs: inget) om det i min bok, och jag hittar inte mycket om det online på varken svenska eller engelska. förstår inte heller vart de har fått denna metoden från? i min kursbok härleds det mesta från variabelseparation. är förvirrad, men blir bara mer och mer förvirrad desto mer jag läser om detta.
undrar om någon skulle kunna komma med något som kan ge röd tråd och struktur, alt. en "skottsäker" metod som man kan ta del av för att lösa dessa typer av problem?
är i dagsläget även öppen till att investera i en ny bok och helt överge kursboken. om någon har tips får ni jätte gärna dela med er
Variabelseparation är ett bra sätt att tackla problemet på. Lösningsförslaget hoppar direkt över till en ansats för lösningen baserat på att problemet har Dirichletvillkor. Detta är ingenting du behöver göra, men går snabbare om du kan det. Efter att ha löst tillräckligt många uppgifter kommer du lära dig vilken form som lösningen borde ha utifrån PDEn och RV+BV. Men variabelseparation funkar som sagt.
Notera att variabelseparation egentligen är ett antagande som inte gäller i alla lägen, men kommer förmodligen gälla i de lägen du stöter på i dessa sammanhang.
Du har gjort helt rätt fram tills sista raden. Exponentialen behöver du inte stryka, sätt bara B=0 samt ett visst krav på lambda så uppfylls RV.
Den generella lösningen är sedan summan över alla n (n är ett heltal som även förekommer i lambda). Därifrån fortsätter du med att sätta in BV för att komma vidare i lösningen.
Entydighet i Fourierserie innebär att koefficienterna uk(t) är unika eftersom att sinus-termerna som förekommer i summan är linjärt oberoende.
Jämför med en punkt i ett vektorrum och en linjärt oberoende bas som spänner upp vektorrummet. Då finns det en entydigt sätt att skriva denna vektor på. I detta fall är sinus-termerna basvektorerna och uk(0) är koefficienterna.
Calle_K skrev:Variabelseparation är ett bra sätt att tackla problemet på. Lösningsförslaget hoppar direkt över till en ansats för lösningen baserat på att problemet har Dirichletvillkor. Detta är ingenting du behöver göra, men går snabbare om du kan det. Efter att ha löst tillräckligt många uppgifter kommer du lära dig vilken form som lösningen borde ha utifrån PDEn och RV+BV. Men variabelseparation funkar som sagt.
Notera att variabelseparation egentligen är ett antagande som inte gäller i alla lägen, men kommer förmodligen gälla i de lägen du stöter på i dessa sammanhang.
Du har gjort helt rätt fram tills sista raden. Exponentialen behöver du inte stryka, sätt bara B=0 samt ett visst krav på lambda så uppfylls RV.
Den generella lösningen är sedan summan över alla n (n är ett heltal som även förekommer i lambda). Därifrån fortsätter du med att sätta in BV för att komma vidare i lösningen.
Entydighet i Fourierserie innebär att koefficienterna uk(t) är unika eftersom att sinus-termerna som förekommer i summan är linjärt oberoende.
Jämför med en punkt i ett vektorrum och en linjärt oberoende bas som spänner upp vektorrummet. Då finns det en entydigt sätt att skriva denna vektor på. I detta fall är sinus-termerna basvektorerna och uk(0) är koefficienterna.
tack så jättemycket! bra med feedback också så vet jag att jag är på rätt spår.
I deras lösningsförslag har de skrivit att "Här ger entydigheten hos fourierserier att" , du råkar inte veta hur de kommit fram till det?
tack återigen!
katal skrev:I deras lösningsförslag har de skrivit att "Här ger entydigheten hos fourierserier att" , du råkar inte veta hur de kommit fram till det?
De jämför helt enkelt VL och HL.
VL kan du utveckla till u1(0)sin(pi*x) + u2(0)sin(2pi*x) + u3(0)sin(3pi*x) + ... Jämför med HL så får du koefficienterna.
Allt gott, bara att återkomma om du har fler funderingar :)
Calle_K skrev:katal skrev:I deras lösningsförslag har de skrivit att "Här ger entydigheten hos fourierserier att" , du råkar inte veta hur de kommit fram till det?
De jämför helt enkelt VL och HL.
VL kan du utveckla till u1(0)sin(pi*x) + u2(0)sin(2pi*x) + u3(0)sin(3pi*x) + ... Jämför med HL så får du koefficienterna.
Allt gott, bara att återkomma om du har fler funderingar :)
Hej igen, fastnat lite på samma uppgift... igen.
Lite oklart vad jag ska göra med denna, min föreläsare burkar skriva att man kan svara med integralen som ett värde på , men i boken har de beräknat den/kommit till ett tydligare svar. Är det några slutsatser jag missat att dra innan integralen här?
 Den analytiska delen av lösningen går sådär.
Den analytiska delen av lösningen går sådär.


