Matematisk modellering: Egenvärden?

Hej!

Har en fråga som lyder:

Lösningen är inget problem, denna lyder:

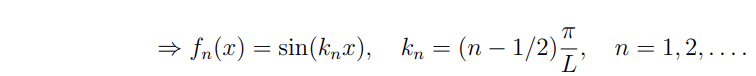
Det enda jag inte förstår är hur de kommit fram till $k_n$ ? hur är $k_n=(n-1/2) \frac { \pi }{L}$ ? Jag förstår allt upp tills de bestämmer $k_n$ , men just den beräkningen känner jag mig inte helt klok på.

Den allmänna lösningen till diffekvationen -f’’² = k²f är f(x) = acoskx + bsinkx.

Använd nu randvillkoren.

f(0) = 0 => a = 0.

f’(L) = bkcoskL = 0 => kL = pi/2, 3pi/2, 4pi/2,… = pi/2 + (n-1)pi, n = 1, 2, 3, … .

Så vi får möjliga k generellt enligt

k_n = (pi/2 + (n-1)pi)/L = (n-1/2)pi/L.

Obs negativa värden på k ger inga oberoende lösningar så de behöver vi inte tänka på.

PATENTERAMERA skrev:
Den allmänna lösningen till diffekvationen -f’’² = k²f är f(x) = acoskx + bsinkx.

Använd nu randvillkoren.

f(0) = 0 => a = 0.

f’(L) = bkcoskL = 0 => kL = pi/2, 3pi/2, 4pi/2,… = pi/2 + (n-1)pi, n = 1, 2, 3, … .

Så vi får möjliga k generellt enligt

k_n = (pi/2 + (n-1)pi)/L = (n-1/2)pi/L.

Obs negativa värden på k ger inga oberoende lösningar så de behöver vi inte tänka på.

Hej!
Jo precis, så långt kom jag också- $f'(L)=Bk_n cos(k_n L)$ men hur kommer man fram till k:s värde i detta fallet? Man vill att $cos(k_n L)=0 => k_n L =1 <=> k_n= \frac {\pi n}{L}$ ?

Vilka lösningar har ekvationen cos(v) = 0? Jo, titta på enhetscirkeln, v = pi/2 + mpi, där m är godtyckligt heltal. Om vi bara är intresserade av positiva lösningar så kan vi skriva v = pi/2 + (n-1)pi, för n = 1, 2, 3… .

Om vi villa lösa cos(kL) = 0 så måste vi ha pss att kL = pi/2 + (n-1)pi = (n-1/2)pi.

Klart som korvspad?

Svara

Visa senaste svar